浅谈深搜
本文同步与洛谷
前言
搜索,本质就是枚举,通过枚举所有可能来找到答案,普通搜索时间复杂度很高,所以有许许多多的优化
搜索是一些高级算法的基础。在 OI 中,纯粹的搜索往往也是得到部分分的手段,但可以通过纯粹的搜索拿到满分的题目非常少。
深度优先搜索DFS
概念
状态:解决问题中所需要关注的属性
转移:状态之间的变化过程
搜索树:状态转移变化过程所形成的树形结构
回溯:回到上一个状态
伪代码
//请结合例题代码,例题题解理解
void dfs(当前状态 x) { // 不一定需要通过参数来获取状态信息
if (x 为非法状态) {
return;
}
for (x 转移出的每个新状态 y) {
dfs(y);
}
}
基本模型
很多搜索题都可以转化成以下三个模型
全排列
例
::::info[题意简要]
按照字典序输出 $1 \sim n$ 的全排列
::::
状态:当前还未生成完毕得排列
转移:在当前全排列后添加一个没有出现过的数
状态转移图(搜索树)如下感谢老师画的图
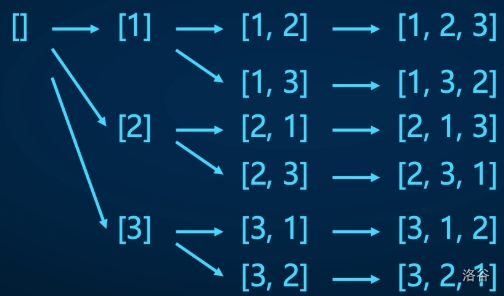
代码:
#include<bits/stdc++.h>
using namespace std;
int n, a[11];//a表示当前全排列
bool v[11];
void dfs(int t){// t表示当前全排列中有多少个数
if(t == n){//有n个表示已经生成完毕
for(int i = 0; i < n; i++){
cout << setw(5) << a[i];
}
cout << '\n';
return ;//结束
}
for(int i = 1; i <= n; i++){
if(!v[i]){//没出现过
v[i] = 1;
a[t] = i;//添加i
dfs(t + 1);//当前有t+1个数
v[i] = 0;//回溯
}
}
}
// 时间复杂度 O(n * n!)
int main(){
ios::sync_with_stdio(0); cin.tie(0);
cin >> n;
dfs(0);//一开始没有数
return 0;
}
复杂度:
空间复杂度:保存全排列和标记每个数字是否使用过,$O(n)$
时间复杂度:共 $n!$ 个全排列,输出时间复杂度 $O(n)$,总时间复杂度为 $O(n \times n!)$,一般适用于 $n \le 10$
补充 next_permutation
next_permutation是 C++ 标准库 <algorithm> 中的函数,用于生成下一个字典序的排列,用法为 next_permutation(首地址,尾地址),过程如下:
- 如果还存在比当前全排列字典序更大的全排列,将其更新为下一个,并返回
true - 如果不存在,将其重置为字典序最小的排列,并返回
false
代码:
#include<bits/stdc++.h>
using namespace std;
int n, a[11];// a表示全排列
int main(){
ios::sync_with_stdio(0); cin.tie(0);
cin >> n;
for(int i = 1; i <= n; i++) a[i] = i;//初始化
do{//第一个排列也的输出,所以得do-while
for(int i = 1; i <= n; i++){
cout << setw(5) << a[i];
}
cout << '\n';
}while(next_permutation(a + 1, a + n + 1));
return 0;
}
子集
例
::::info[题意简要]
按字典序输出 ${ 1,2,...,n}$ 的子集
::::
状态:目前子集与当前考虑 $t$ 是否在子集内
转移:加入子集与不加入
搜索树如下(可恶的老师竟然不画图)
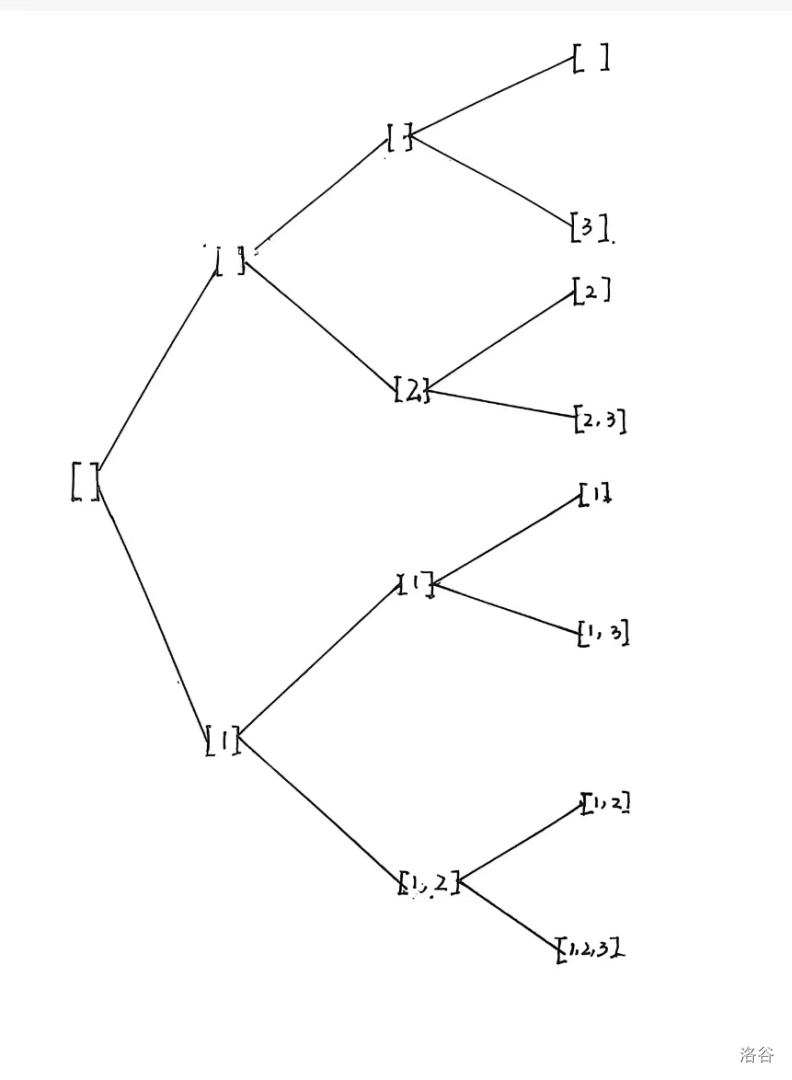
代码:
#include<bits/stdc++.h>
using namespace std;
int n;
vector<int> v;// v是子集
vector<vector<int>> ans;//答案
void dfs(int t){//表示在考虑t
if(t == n + 1){//考虑完了
ans.push_back(v);// 记录在答案中
return ;//结束
}
dfs(t + 1);//不选
v.push_back(t);
dfs(t + 1);//选
v.pop_back();//回溯
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n;
dfs(1);//先考虑1
sort(ans.begin(), ans.end());//按字典序排序
for(auto x : ans){
for(int y : x){//C++11新特性
cout << y << ' ';
}
cout << '\n';
}
return 0;
}
复杂度:
- 空间:
每个递归 $O(1)$,$n$ 层递归 $O(n)$,记录子集 $O(n)$。 - 时间:
枚举所有子集 $O(2^n)$,输出最坏 $O(n)$,总时间复杂度为 $O(n\times2^n)$,一般适用于 $n \le 20$
网格图
例
::::info[题意简要]
给定一个带障碍的迷宫,每次可以从当前格子移动到相邻的一个非障碍格子,求起点到终点的方案数。
::::
状态:当前坐标 $(x,y)$
转移:往四个方向走
搜索树太难画了,我们就不画了
代码:
#include<bits/stdc++.h>
using namespace std;
const int dx[] = {1, -1, 0, 0};
const int dy[] = {0, 0, -1, 1};//方向数组
int n, m, t, sx, sy, fx, fy, xx, yy, ans;
bool vis[7][7];//格子是否能走
void dfs(int x, int y){
if(x < 1 || x > n || y < 1 || y > m || vis[x][y]) return ;// 判断状态是否超出边界、状态是否遍历过
if(x == fx && y == fy){
ans++;
return;
}
vis[x][y] = 1;//标记走过
for(int i = 0; i < 4; i++){
dfs(x + dx[i], y + dy[i]);
}
vis[x][y] = 0;//回溯
}
int main(){
ios::sync_with_stdio(0); cin.tie(0);
cin >> n >> m >> t >> sx >> sy >> fx >> fy;
while(t--){
cin >> xx >> yy;
vis[xx][yy] = 1;
}
dfs(sx, sy);//从起点开始
cout << ans;
return 0;
}
深搜剪枝
你得先把前面学懂,剪枝可以去看看这篇文章
深搜的复杂度都是指数级的,很难满足题目要求,因此我们需要一种最简单的优化——剪枝
搜索的进程可以看作从搜索树的树根出发,遍历一棵树的过程,剪枝就是去除一些不必要的过程。
剪枝一般分可行性剪枝,最优性剪枝,卡时,记忆化搜索
可行性剪枝
将不合法的状态,以及不能得到一个合法的答案的搜索树剪掉,即return。
伪代码:
//请结合例题代码,例题题解理解
void dfs(...){
if(当前状态不符合要求)
return;
...
}
例
状态:当前数与位数
转移:往后添加一位数
剪枝:如果当前数不是质数后面就都不符合要求
代码:
#include<bits/stdc++.h>
using namespace std;
int n;
bool check(int x){
for(int i = 2; i * i <= x; i++){
if(!(x % i)){
return 0;
}
}
return x > 1;
}//判断质数
void dfs(int ans, int cnt){//当前数为ans,有cnt位
if(!check(ans))//如果不是质数后面就都不符合要求
return ;
if(cnt == n){//搜索完毕
cout << ans << '\n';
return;
}
for(int i = 0; i <= 9; i++){
dfs(ans * 10 + i, cnt + 1);//往后添加一位
}
}
int main(){
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
dfs(2, 1), dfs(3, 1), dfs(5, 1), dfs(7, 1);//开头只能是2,3,5,7
return 0;
}
最优性剪枝
可以分为全局最优性剪枝和局部最优性剪枝。
全局最优性剪枝
如果当前答案不比目前所得答案更优,且继续搜下去答案不会更优时,将其剪掉
伪代码:
//请结合例题代码,例题题解理解
void dfs(...){
if(当前答案不比目前答案更优)
return;
...
}
例
这道题类似于全排列,可以模仿全排列的模板。
状态:当前坐标,当前距离总和,选了多少个点。
转移:枚举下一个点,更新总距离(距离公式看后记)
剪枝:若当前总距离不比目前答案更短,return
代码:
#include<bits/stdc++.h>
using namespace std;
using db = double;
int n;
bool vis[20];//全排列模板标记数组
db ans = 1e9, x[20], y[20];
void dfs(db lx, db ly, int s, db dis){//lx,ly表坐标,s表选的个数,dis表当前距离
if(dis >= ans){//剪枝
return ;
}
if(s == n){//结束
ans = dis;
return ;
}
for(int i = 1; i <= n; i++){
if(!vis[i]){
vis[i] = 1;
dfs(x[i], y[i], s + 1, dis + sqrt((x[i] - lx) * (x[i] - lx) + (y[i] - ly) * (y[i] - ly)));
vis[i] = 0;
}
}
}
int main(){
cin >> n;
for(int i = 1; i <= n; i++){
cin >> x[i] >> y[i];
}
dfs(0, 0, 0, 0);
cout << fixed << setprecision(2) << ans;
return 0;
}
这样交会 $90pts TLE$,怎么优化呢?我们先放一放
局部最优性剪枝
当前答案不比上次搜到这个状态的答案更优,将其剪掉
伪代码:
//请结合例题代码,例题题解理解
void dfs(...){
if(当前答案不比上次搜到这个状态的答案更优)
return;
更新当前状态的答案
...
}
状态:当前坐标与步数
转移:走,步数+1
剪枝:如果当前步数不比上一次走到当前位置的步数更少,剪枝
代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 4e2 + 5;
const int dx[] = {1, 1, 2, 2, -1, -1, -2, -2};
const int dy[] = {2, -2, 1, -1, 2, -2, 1, -1};
int n, m, sx, sy, dis[N][N], cnt;
void dfs(int x, int y, int d){//x,y为坐标,d为步数
if(x < 1 || x > n || y < 1 || y > m || d >= dis[x][y]){
return ;
}
dis[x][y] = d;//最优化数组
for(int i = 0; i < 8; i++){
dfs(x + dx[i], y + dy[i], d + 1);
}
}
int main(){
cin >> n >> m >> sx >> sy;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
dis[i][j] = INT_MAX;//初始化
}
}
dfs(sx, sy, 0);
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
cout << (dis[i][j] == INT_MAX ? -1 : dis[i][j]) << ' ';
}
cout << '\n';
}
return 0;
}
这样做只能拿 $90$ 分,不过 $90$ 分够了,等会你还会遇到它
卡时
在以上剪枝的基础上,如果代码快超时了,就直接输出解。各位想吃奶酪的盆友们,我们只要卡时就能过前面的数据。
代码:
#include<bits/stdc++.h>
using namespace std;
using db = double;
int n, cnt;
bool vis[20];
db ans = 1e9, x[20], y[20];
void dfs(db lx, db ly, int s, db dis){
if(dis >= ans || cnt >= 1e7){
return ;
}
if(s == n){
ans = dis;
return ;
}
cnt++;
for(int i = 1; i <= n; i++){
if(!vis[i]){
vis[i] = 1;
dfs(x[i], y[i], s + 1, dis + sqrt((x[i] - lx) * (x[i] - lx) + (y[i] - ly) * (y[i] - ly)));
vis[i] = 0;
}
}
}
int main(){
cin >> n;
for(int i = 1; i <= n; i++){
cin >> x[i] >> y[i];
}
dfs(0, 0, 0, 0);
cout << fixed << setprecision(2) << ans;
return 0;
}
但还有两个点过不去怎么办?那就不过了,因为它是专门来hack你的,此题正解为状压DP或记忆化。
记忆化
在搜索中,如果传入相同的值会得到相同的结果,我们可以记录下每个状态的答案,当多次访问到某个状态时,可直接给出结果,这种搜索通常带返回值。
伪代码:
//请结合例题代码,例题题解理解
int dfs(...){
if(当前状态被访问过)
return ...;
...
更新当前状态的答案
return 当前状态的答案;
}
例
状态:考虑前几种药,用了多少时间,返回最大价值。
转移:采,不采当前这种药。
代码:
#include<bits/stdc++.h>
using namespace std;
int t, m, a[101], b[101], res[101][1001];
int dfs(int x, int u){//考虑前x种药,u表示所用时间,返回最大价值
if(x == m + 1)//先判越界
return 0;
if(res[x][u] != -1)//被访问过
return res[x][u];
int dfs1 = dfs(x + 1, u);//不采
int dfs2 = -1;//有可能不能采,得先用无效值
if(u + a[x] <= t)//能采
dfs2 = dfs(x + 1, u + a[x]) + b[x];
return res[x][u] = max(dfs1, dfs2);
}
int main(){
ios::sync_with_stdio(0); cin.tie(0);
memset(res, -1, sizeof res);//初始无效值
cin >> t >> m;
for(int i = 1; i <= m; i++){
cin >> a[i] >> b[i];
}
cout << dfs(1, 0);
return 0;
}
flood-fill
$\text{flood-fill}$,又称状态图遍历,就是每个状态只需遍历一次,无需回溯! 这种问题通常处理每个状态是否可以转移得到。
伪代码:
void dfs(当前状态 x) {
if (x 非法,或当前状态 x 已遍历过) {
return;
}
标记当前状态 x 已遍历;
for (x 转移出的每个新状态 y) {
dfs(新状态 y);
}
}
例1
思路:
从一个没被遍历过的含水格子开始搜索,遍历所有相连的格子。
状态:当前坐标
转移:八个方向走
代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 1e2 + 5;
const int dx[] = {0, 0, 1, 1, 1, -1, -1, -1};
const int dy[] = {1, -1, 1, 0, -1, 1, 0, -1};//方向数组
int n, m, ans;
char c[N][N];
void dfs(int x, int y){//当前坐标
if(x < 1 || x > n || y < 1 || y > m || c[x][y] == '.'){
return ;
}
c[x][y] = '.';//标记被遍历过
for(int i = 0; i < 8; i++){
dfs(x + dx[i], y + dy[i]);//转移
}
// 不能写 c[x][y] = '#';
}
int main(){
ios::sync_with_stdio(0); cin.tie(0);
cin >> n >> m;
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
cin >> c[i][j];
}
}
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
if(c[i][j] == 'W'){
ans++;
dfs(i, j);
}
}
}
cout << ans;
return 0;
}
复杂度:
- 时间:
每个点至多被遍历一次,每个点转移八次,复杂度为 $O(n\times m + 8 \times n \times m = 9\times n \times m) = O(n \times m)$ - 空间:$O(n \times m)$
状态:当前数 $x$
转移:$x \to 2x + 7,x\to x^2+9$
代码:
#include<bits/stdc++.h>
using namespace std;
const int N = 5e6 + 1;
int n, k;
vector<int> ans;//答案集合
bool v[N];
void dfs(int x){//当前填充数字
if(x < 0 || x >= k || v[x])//x <= 0判爆int,v[x] 判是否重复
return ;
v[x] = 1;//标记在集合内
ans.push_back(x);//记录答案
dfs(2 * x + 7);
dfs(x * x + 9);//转移
//不回溯
}
int main(){
ios::sync_with_stdio(0), cin.tie(0);
cin >> n >> k;
dfs(n);
cout << ans.size() << '\n';
sort(ans.begin(), ans.end());//按大小从小到大排序
for(int it : ans)//c++11新语法
cout << it << ' ';
return 0;
}
空间复杂度:$O(k)$
时间复杂度:$1\sim k$ 中的数每个至多遍历一次,复杂度 $O(k)$
后记
距离公式:
$dis((x1,y1),(x2,y2))=\sqrt{(x1-x2)2+(y1-y2)2}$
没更新完,我可以不帮你们找题吗?



 浙公网安备 33010602011771号
浙公网安备 33010602011771号