AVL树

#include <stdio.h>
#include <stdlib.h>

#define max(a, b)  (((a) > (b)) ? (a) : (b)) 


// 定义树节点结构体
typedef struct TreeNode {
    int key;
    struct TreeNode *left;
    struct TreeNode *right;
    int height;  // 节点的高度
} TreeNode;

// 计算节点的高度
int height(TreeNode *node) {
    if (node == NULL) {
        return 0;
    }
    return node->height;
}


// 创建新节点
TreeNode *newNode(int key) {
    TreeNode *node = (TreeNode *)malloc(sizeof(TreeNode));
    node->key = key;
    node->left = node->right = NULL;
    node->height = 1;  // 新节点的高度为1
    return node;
}

// 获取节点的平衡因子
int getBalance(TreeNode *node) {
    if (node == NULL) {
        return 0;
    }
    return height(node->left) - height(node->right);
}

// 右旋转子树
TreeNode *rightRotate(TreeNode *y) {
    TreeNode *x = y->left;
    TreeNode *T2 = x->right;

    // 执行旋转
    x->right = y;
    y->left = T2;

    // 更新节点高度
    y->height = max(height(y->left), height(y->right)) + 1;
    x->height = max(height(x->left), height(x->right)) + 1;

    return x;
}

// 左旋转子树
TreeNode *leftRotate(TreeNode *x) {
    TreeNode *y = x->right;
    TreeNode *T2 = y->left;

    // 执行旋转
    y->left = x;
    x->right = T2;

    // 更新节点高度
    x->height = max(height(x->left), height(x->right)) + 1;
    y->height = max(height(y->left), height(y->right)) + 1;

    return y;
}

// 插入节点
TreeNode *insert(TreeNode *node, int key) {

    if (node == NULL) {
        return newNode(key);
    }

    if (key < node->key) {
        node->left = insert(node->left, key);
    } else if (key > node->key) {
        node->right = insert(node->right, key);
    } else {
        // 重复的键不允许插入
        return node;
    }

    // 更新节点的高度
    node->height = 1 + max(height(node->left), height(node->right));

    // 获取节点的平衡因子
    int balance = getBalance(node);

    // 左重右轻，需要右旋转
    if (balance > 1 && key < node->left->key) {
        return rightRotate(node);
    }

    // 右重左轻，需要左旋转
    if (balance < -1 && key > node->right->key) {
        return leftRotate(node);
    }

    // 左重右重，需要左右旋转
    if (balance > 1 && key > node->left->key) {
        node->left = leftRotate(node->left);
        return rightRotate(node);
    }

    // 右重左重，需要右左旋转
    if (balance < -1 && key < node->right->key) {
        node->right = rightRotate(node->right);
        return leftRotate(node);
    }

    // 树保持平衡，返回不变的根节点
    return node;
}

// 中序遍历树
void inOrder(TreeNode *root) {
    if (root != NULL) {
        inOrder(root->left);
        printf("%d %d\n", root->key, root->height);
        inOrder(root->right);
    }
}

int main() {
    TreeNode *root = NULL;

    // 插入节点
    root = insert(root, 10);
    root = insert(root, 20);
    root = insert(root, 30);
    root = insert(root, 15);
    root = insert(root, 5);
    root = insert(root, 9);
    root = insert(root, 3);

    // 中序遍历树，打印排序后的节点
    inOrder(root);
    return 0;
}

输出结果

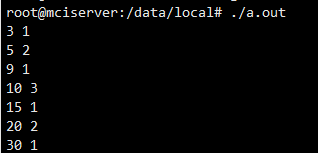
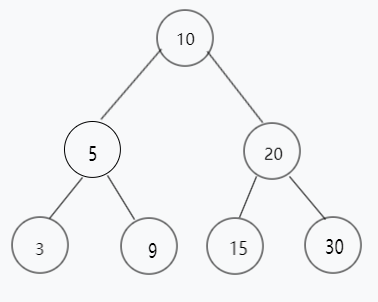
根据输出我们得知,key=10的节点高度为3,key=5 和 key=20的高度为2, 以此类推得到二叉平衡树图如下