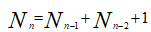Chapter 3 树与二叉树
Chapter 3 树与二叉树
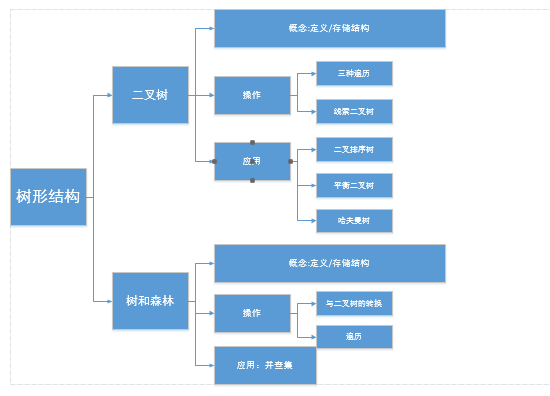
1- 二叉树
主要性质：
1 叶子结点数 = 度为2的结点数 + 1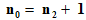 
2 二叉树第i层上最多有 (i≥1)个结点
3 深度为k的二叉树最多有 个结点
2- 二叉树的链式存储结构&&遍历
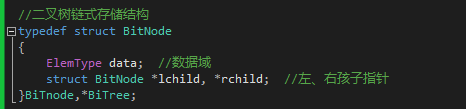
1 链式存储结构
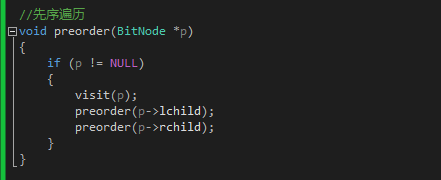
2 先序
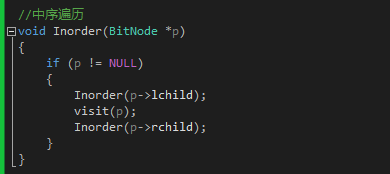
3 中序
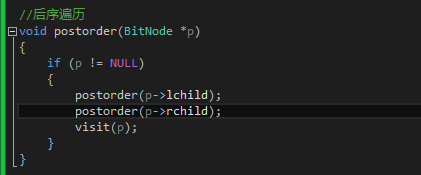
4 后序
3- 线索二叉树
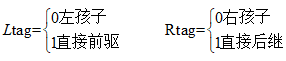
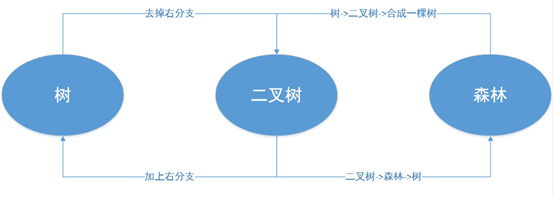
4- 树、二叉树、森林之间的转换
5- 树和森林的遍历
6- 树与二叉树的应用
1） 二叉排序树（查找/搜索）BST == Binary Sort/Search Tree
1 插入：一定是叶结点
2 删除：
叶子->直接删
只有一棵子树->删掉后接上子树
既有左子树，又有右子树->找到右子树最左结点/左子树最右结点代替它，然后删去。
3 查找效率分析
l 二叉排序树的ASL，主要取决于树高。
l 与二叉查找判定树相似，但二分唯一，二叉不唯一。
l 当有序表静态查找时，宜顺序表存储
l 二分查找动态查找时，宜二叉排序树
2） 平衡二叉树(AVL树)
平均查找长度ASL O(log2n)
3） 哈夫曼树(最优二叉树)
产生最短前缀码
注：
1- 树的路径长度是所有路长度的总和
Huffman的带权路径长度：根结点到任意结点的路径长度（经过的边数）与该结点上权值的乘积。
2- 二叉树与度为2的树不同。
3- 三种遍历时间复杂度O(n)
二叉排序树O(logn)
AVL树O(logn)
4- 栈：递归->非递归
队列：层次遍历
5- 先、中序/中、后序/中、层序，可唯一确定一棵二叉树
6- 前、中线索二叉树不再需要栈的支持，后序线索二叉树仍需要
7- 平衡二叉树结点递推公式
