Educational Codeforces Round 108 (Rated for Div. 2) E. Off by One
一、题目大意
给你n个点,每个点可以且必须进行一次位移(横向向右移动一个单位或者纵向向上移动一个单位),问位移之后有多少对点可以进行匹配(只要两个点和原点三点共线即可匹配),每个点只能匹配一次,问最大匹配数目和匹配方案。
样例1也强调了,每个点只能匹配一次,且可能有重合点,每个点也必须要移动。
二、算法分析
①采用tan值的方式衡量是否共线,由尽量避免小数出现的原则,tan值可以用分数结构体来刻画。
②化点为边,一个点有两种平移方式,那么就可以用一条斜边来代替原图中的一个点,如图所示

对于斜边来说,两个端点就是原来的点唯二能移动到的地方。那么问题就由点匹配转化为了边匹配。
将新图称为形式图,将原图称为坐标图。
对于形式图的边匹配,两条边要匹配,则必然有一个公共点进行衔接,这个公共的定义从实际出发,并不意味着两条边挨在一起。如图所示
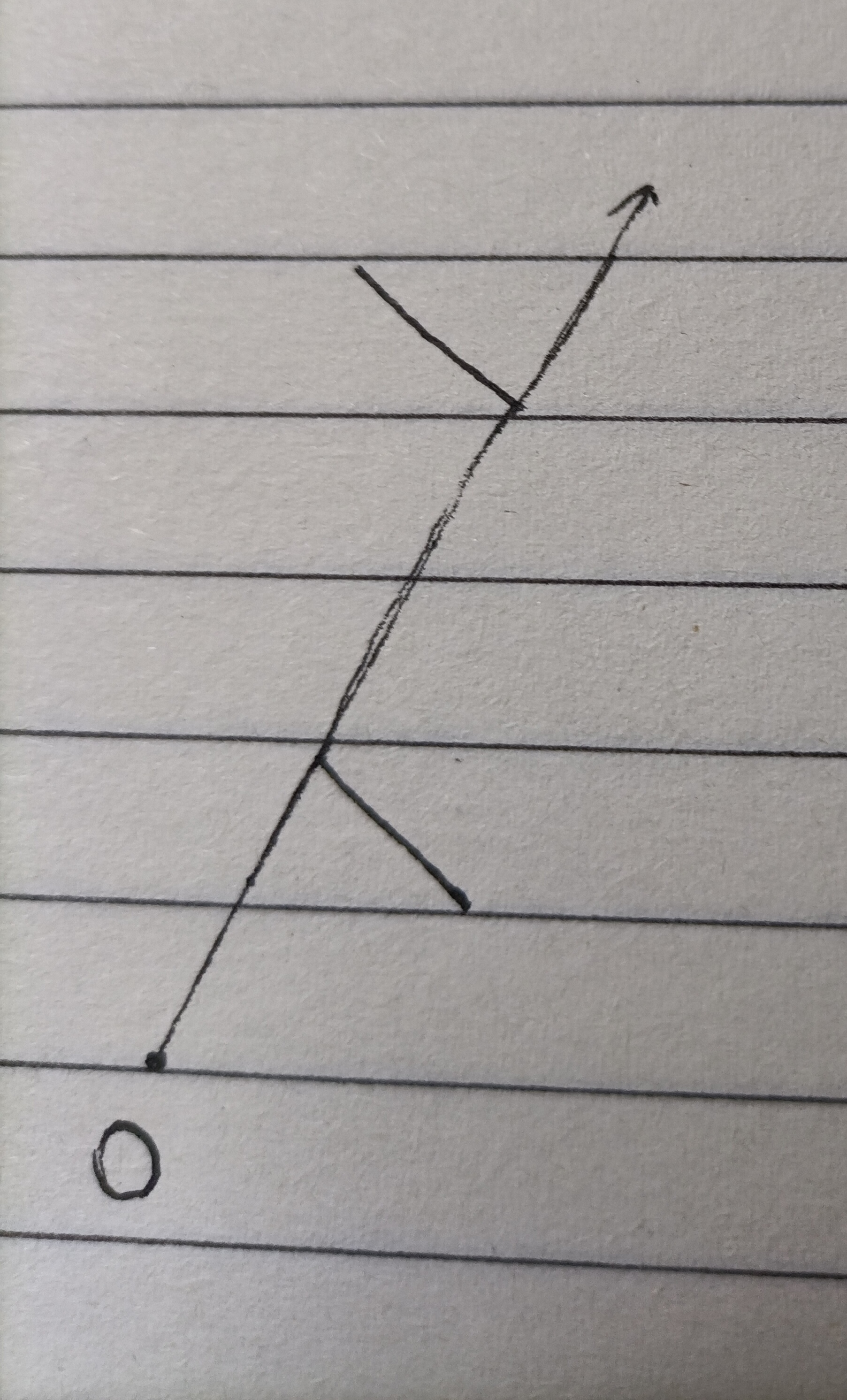
假设从原点射出无数条射线,其中有一条是最后的三点共线,如果恰好把形式图中的两条边连起来了,则认为连接点是公共点。记这样的点为形式图中的枢轴点,对于本题,tan值相同的点是枢轴点。(如上图中射线上的除原点外的另外两个连接点是公共点)
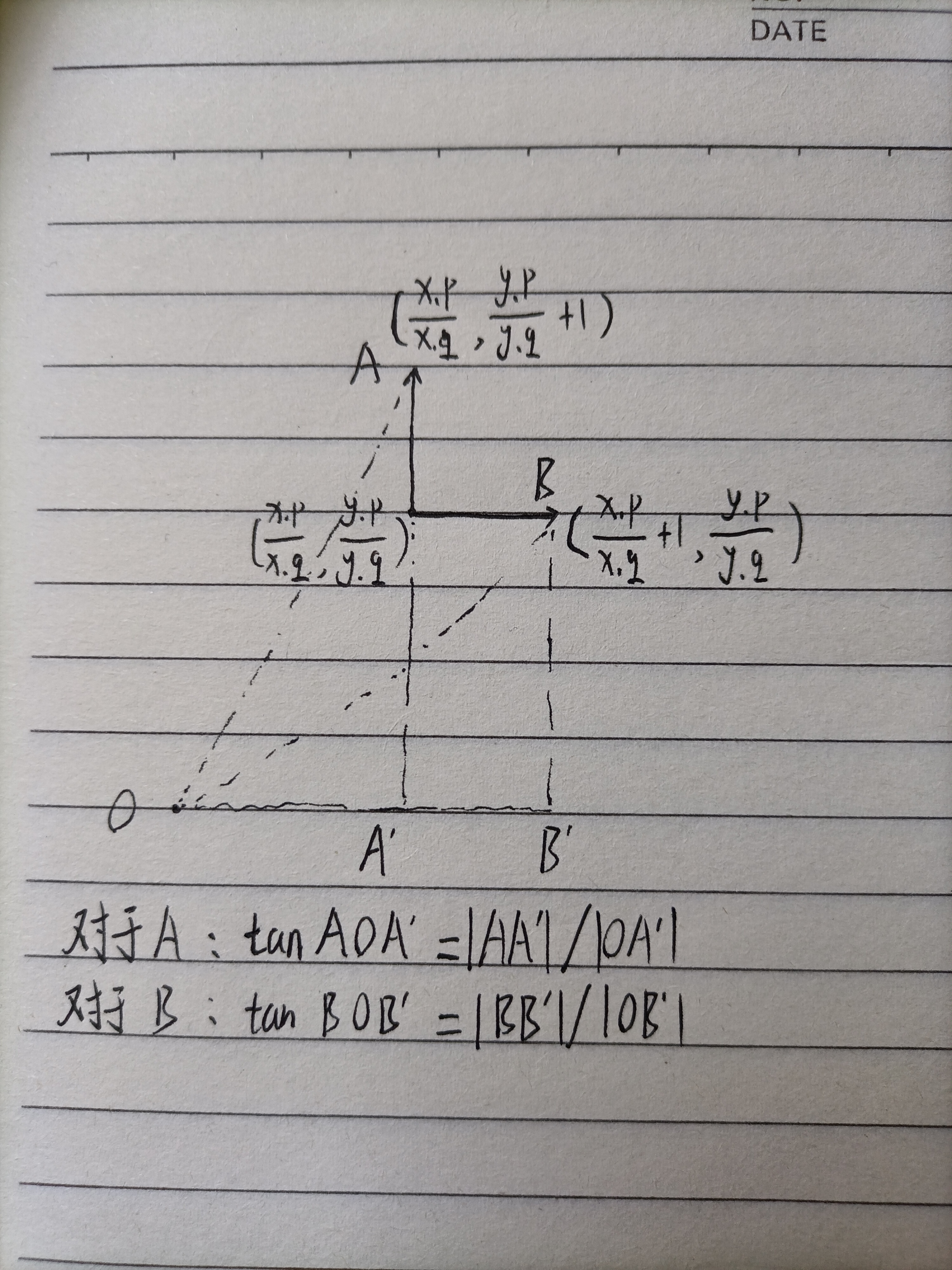
形式图上的边的端点的tan值计算方法如下图所示:
③用dfs进行匹配,这也是本题的难点
这里先复习一下dfs过程中的几种边
https://oi-wiki.org/graph/scc/
有一个性质,返祖边(后向边)的两端点在dfs中的深度不同,且返祖边会走到一个深度更小的点。
然后是比较简单的贪心策略,如图所示
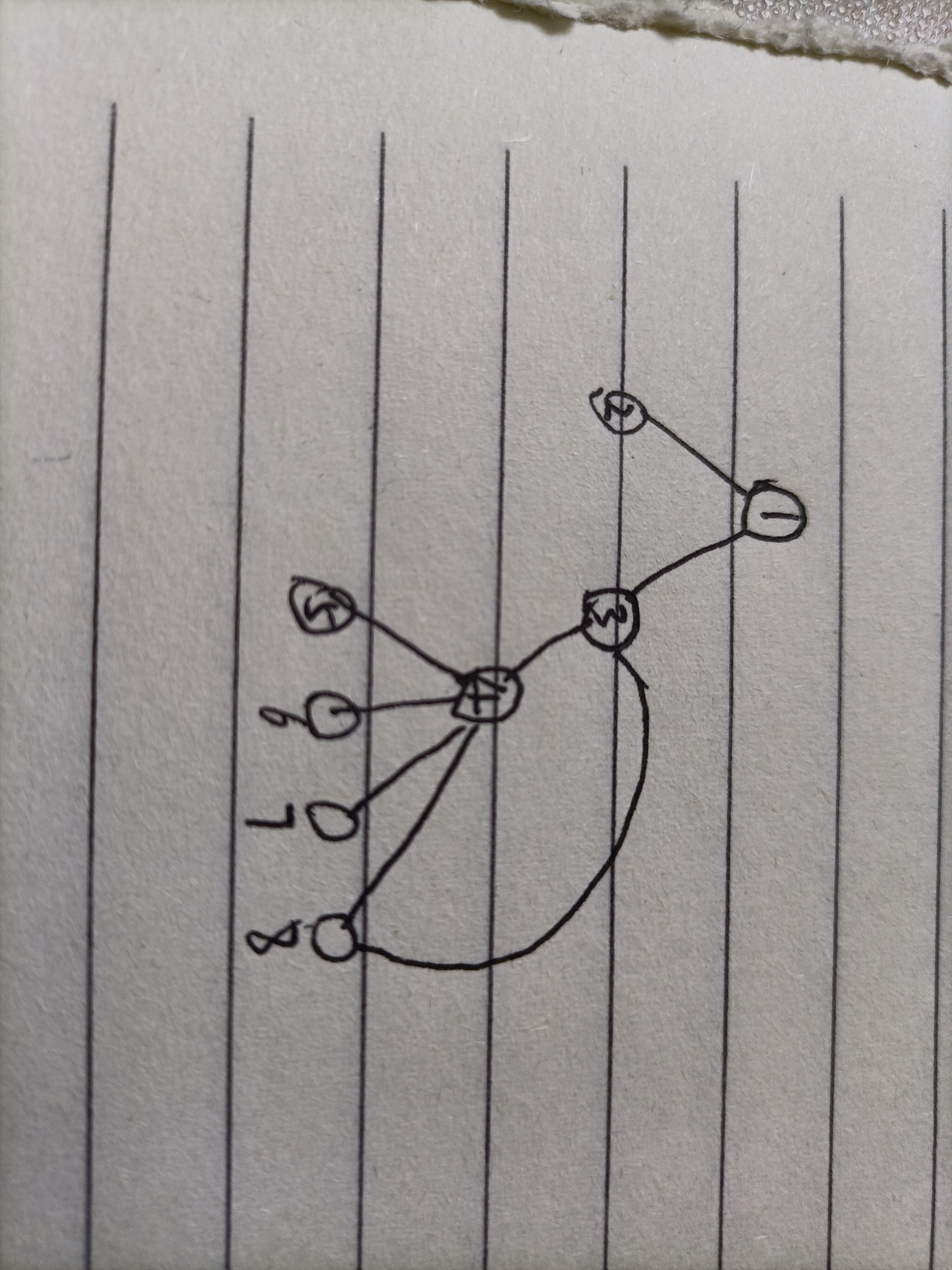
以上的每个结点都是形式图上的枢轴点。对于8到3的无向边,就是一条返祖边。贪心策略是对于某个点,如果其下辖的边(包括树枝边和返祖边,下同)个数为偶数,则以该点为公共点,就可以使得下辖的边互相匹配。而如果是奇数,则将下辖边中多出的一条边与该点的父结点到该点的这条边(以下定义为直连边)相匹配。那么如果一个结点下辖的边个数为偶数,则其直连边留给其父结点用。
dfs向下过程中只会经过树枝边,因此要特殊处理其它类型的边,因为返祖边也属于下辖边。
然后对于两种特殊的边的处理方式:
因为返祖边会走到一个深度更小的点,所以可以分出来这条边是横叉边还是返祖边。
横叉边:不进行遍历
返祖边:归到其祖宗,因为其也是祖宗结点下辖的边,也可以参与匹配
三、代码及注释
1 #include<iostream> 2 #include<cstring> 3 #include<algorithm> 4 #include<cstdio> 5 #include<vector> 6 #include<map> 7 #define LL long long 8 using namespace std; 9 const int N=500050; 10 const int M=N<<2; 11 struct Fraction{ //首先是分数结构体 12 LL p,q; 13 bool operator <(const Fraction &t) const{ //记得要放到map里就是得可比较的 14 return (long double)p/q <(long double)t.p/t.q; 15 } 16 }; 17 LL gcd(LL x,LL y){ 18 return y==0 ? x : gcd(y,x%y); 19 } 20 Fraction reduce(Fraction a){ //约分 21 LL temp=gcd(a.p,a.q); 22 Fraction fraction={a.p/temp,a.q/temp}; 23 return fraction; 24 } 25 map<Fraction,int> dict; //映射一个字典 26 int n; 27 int cnt; 28 int get_id(Fraction x){ 29 if(dict.count(x)) return dict[x]; 30 dict[x]=++cnt; 31 return cnt; 32 } 33 int h[M],e[M],ne[M],idx; //建立形式图 34 int G[M]; 35 void add(int a,int b,int id){ 36 e[idx]=b,ne[idx]=h[a],h[a]=idx; 37 G[idx]=id; 38 idx++; 39 } 40 void read(){ 41 memset(h,-1,sizeof(h)); 42 scanf("%d",&n); 43 for(int i=1;i<=n;i++){ 44 LL p1,q1,p2,q2; 45 scanf("%lld%lld%lld%lld",&p1,&q1,&p2,&q2); 46 Fraction x=reduce((Fraction){p1,q1}); //x和y是原图上点的两个坐标 47 Fraction y=reduce((Fraction){p2,q2}); 48 Fraction a,b; //a和b是对应形式图的边的两个端点的tan值,a是向上的,b是向右的 49 a.p=(y.p+y.q)*x.q; 50 a.q=y.q*x.p; 51 b.p=y.p*x.q; 52 b.q=y.q*(x.p+x.q); 53 int u=get_id(a); 54 int v=get_id(b); 55 //cout<<u<<' '<<v<<endl; 56 //cout<<a.p<<' '<<a.q<<' '<<b.p<<' '<<b.q<<endl; 57 add(u,v,i); 58 add(v,u,i); 59 } 60 } 61 int depth[N]; 62 vector<int> edges[N]; //存形式图上以点i为连接点的边对应的原图上的点,由于每对匹配边必然有同一个连接点,所以最终答案是edges数组大小/2 63 void dfs(int u,int fa){ 64 int pre_node=-1; //直连边的端点对应的形式图的边对应的原图的点编号 65 depth[u]=depth[fa]+1; 66 for(int i=h[u];~i;i=ne[i]){ 67 int j=e[i]; 68 if(!depth[j]) dfs(j,u); //如果到了一个未经过的点,则往后dfs(写这里的时候,不小心把u和j写反了,然后调了一个多小时其它的地方,之后还是要记得出现bug先通读代码) 69 else{ //否则就是横叉边或者返祖边 70 if(depth[j]>depth[u]) continue; //横叉边 71 else if(j==fa && pre_node==-1){ //第一条直连边按直连边算,其它的重边按返祖边算 72 pre_node=G[i]; 73 } 74 else{ 75 edges[j].push_back(G[i]); //返祖边 76 } 77 } 78 } 79 if(fa){ //考虑直连边 80 if(edges[u].size() & 1){ //如前述算法分析里面,对树枝边分成奇数和偶数的情况 81 edges[u].push_back(pre_node); 82 } 83 else{ 84 edges[fa].push_back(pre_node); 85 } 86 } 87 } 88 void print(){ 89 int res=0; 90 for(int i=1;i<=cnt;i++){ 91 res+=edges[i].size()/2; 92 } 93 cout<<res<<endl; 94 for(int i=1;i<=cnt;i++){ 95 for(int j=0;j+1<edges[i].size();j+=2){ 96 printf("%d %d\n",edges[i][j],edges[i][j+1]); 97 } 98 } 99 } 100 int main(){ 101 102 read(); 103 for(int i=1;i<=cnt;i++) 104 if(!depth[i]) dfs(i,0); //图不一定连通 105 print(); 106 107 108 return 0; 109 110 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号