06-图
1.学习总结
1.1图的思维导图
1.2 图结构学习体会
-
深度遍历算法
利用深度优先搜索算法可以求得相应拓扑排序表，利用拓扑排序表可以方便的解决很多图有关的问题，像最大路径问题等等。 -
广度遍历算法
深度优先遍历是将某一条枝桠上的所有节点都搜索到了之后，才转向搜索另一条枝桠上的所有节点，而广度优先遍历是以层为顺序，将某一层上的所有节点都搜索到了之后才向下一层搜索，所以可以解决像六度空间这类问题 -
Prim和Kruscal算法
prim函数用到了两个辅助数组，lowcost[k]保存V-U中编号为k的顶点到U中所有顶点的最小权值。closest[k] 保存着U中到V-U中编号为K的顶点权值最小的顶点的编号。这两个数组的元素是随着顶点不断加入U集合而动态变化的。这个算法中采用邻接矩阵法创建图。
Kruskal算法基于贪心算法，把所有的边按照权值先从小到大排列，接着按照顺序选取每条边，如果这条边的两个端点不属于同一集合，那么就将它们合并，直到所有的点都属于同一个集合为止，合并用到了并查集 -
Dijkstra算法
Dijkstra算法用于计算一个节点到其他所有节点的最短路径，以起始点为中心向外层层扩展，直到扩展到终点为止。 -
拓扑排序算法
如果按照拓扑序列中的顶点次序，在开始每一项活动时，能够保证它的所有前驱活动都已完成，从而使整个工程顺序进行，不会出现冲突的情况，所以适合活动场地的安排，活动顺序的安排等等。
2.PTA实验作业
2.1 题目1：图着色问题
2.2 设计思路
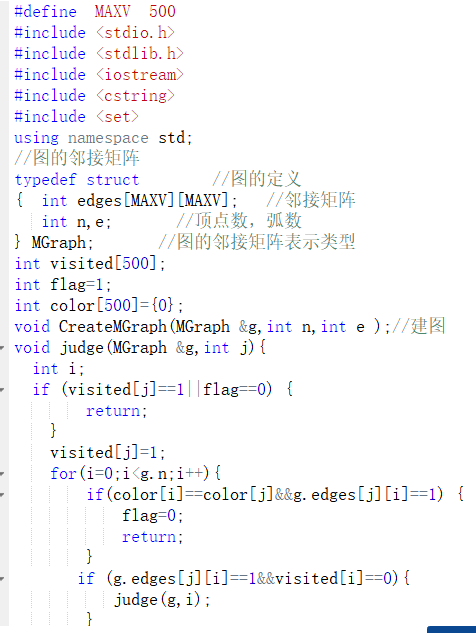
创建邻接矩阵
输入要查询的颜色方案种类sum
for i=0 to i=sum
定义容器s存放颜色
循环输入顶点颜色
如果颜色没出现过，就存入s
判断顶点颜色总数
如果不等于规定的颜色种类，输出No
如果等于规定颜色种类
从每个顶点出发进行遍历，只要边俩个顶点颜色相同，就结束循环，输出No
否则输出Yes
end for
2.3 代码截图
2.4 PTA提交列表说明。
写这题遇到俩个难点
- 怎么判断着色方案可行
这一题上课有讨论过，就是利用遍历来判断，要判断相邻顶点颜色是否相同，所以利用深度遍历，查找邻接点 - 怎么计算颜色种类
判断相邻顶点是否有颜色相同的后，测试数据时发现没有考虑颜色种类的限制。一开始我想的是利用数组，有相同的颜色就不加入，没有就加入数组，最后判断数组长度。但是操作好像有点麻烦，怎么修改结果都不对，思路也没发现哪不对，尝试交了一次，果然答案错了。。。所以百度借鉴了代码，用到了set，利用s.insert存放颜色，s.size()存放颜色种类
2.1 题目2：六度空间
2.2 设计思路
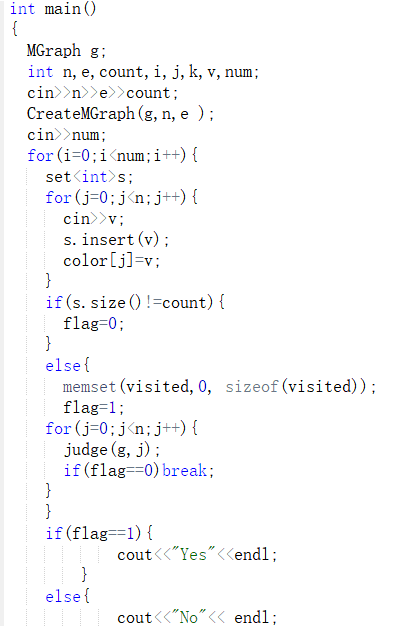
定义顶点数n,边数e
创建邻接矩阵
循环每个顶点
定义变量 i,num,j，count，num用来记录层数，count记录相邻顶点数，初值为1
定义队列q
记录顶点状态，已经访问过
将顶点入队
for num=0 to num=6
定义数组 vec
队列不为空时
取队首元素，存入vec,出队队首
遍历数组vec
找到数组元素在图中的边并且另一个顶点没被访问过
将顶点入栈，记录顶点已经被访问
count++
六层循环结束后
计算比例
2.3 代码截图
2.4 PTA提交列表说明。
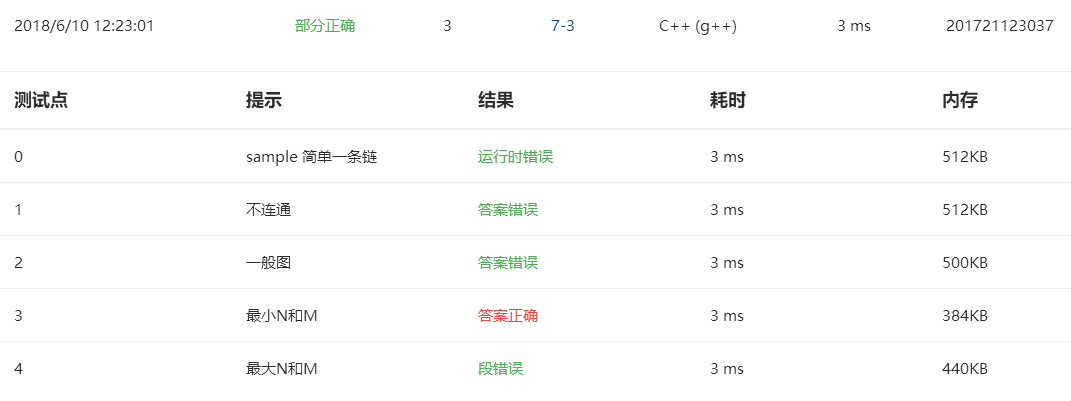
我想的是找到顶点的邻接点，这些邻接点再继续找它们的邻接点，一直这样找下去，找六次。这些所有找到的顶点数和总数的比值就是我们要求的，一开始用的是数组记录，但是结果不对，我有输出每一次找到的顶点数，和用容器输出的差别很大，每次都是1，后来也改用了容器，但是不理解为什么都有memset( visit, 0, sizeof(visit[0])*(n+1))，而且删了结果就不对了，循环次数好像少了
2.1 题目3：道路村村通
2.2 设计思路
输入顶点数和边数
如果边数小于顶点数减一，输出-1
否则
构建邻接数组
定义距离数组dis和存放前一个顶点的数组pre
对顶点数组pre初始化，都为-1
距离数组dis初始化，为顶点1到其他顶点的距离
给dis[1]赋值为0，pre[1]赋值为0
循环变量i从顶点2到顶点n
在所有顶点中找出离顶点i最近的顶点，记录最近编号k，修改距离为最短距离
记录顶点k前一个顶点i
累加每次找到的最短距离
遍历距离数组，如果图中存在到达该顶点更小的距离，要修改数组
如果最终距离和大于INF说明图不连通，输出-1
否则输出距离
2.3 代码截图
2.4 PTA提交列表说明。
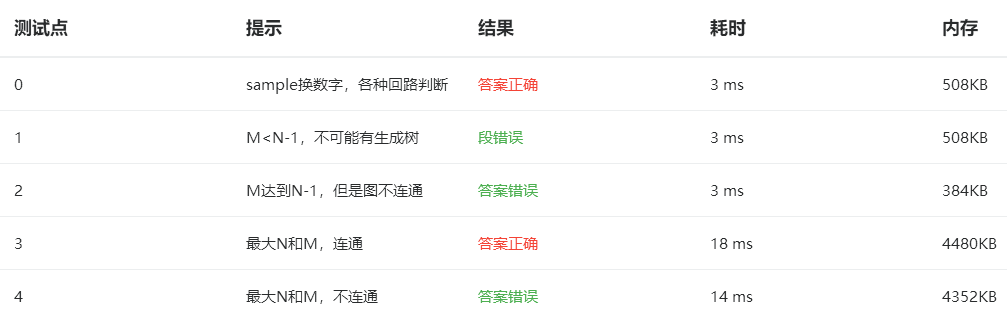
没有考虑图不连通和构不成图的情况
- 图不连通
因为初始化为INF,所以图不连通的话，路径和一定大于INF - 构不成图
一开始没想到可以用顶点数和边数的关系来判断，要想构成连通图，至少有顶点数-1的边数
3.截图本周题目集的PTA最后排名
3.1 PTA排名
3.2 我的总分：1.5
4. 阅读代码
代码：求俩条路线，一条是最快到达路线，一条是最短距离的路线
代码链接：https://blog.csdn.net/m0_38015368/article/details/78450727
- 带权邻接矩阵的初始化，对角是0，其余为无穷大
- 路径利用了递归，推导出所有顶点之间的最短路径
- 注意修改最短路径
- 核心算法是弗洛伊德算法
