2022面向对象第一单元总结

第一次作业

核心类图

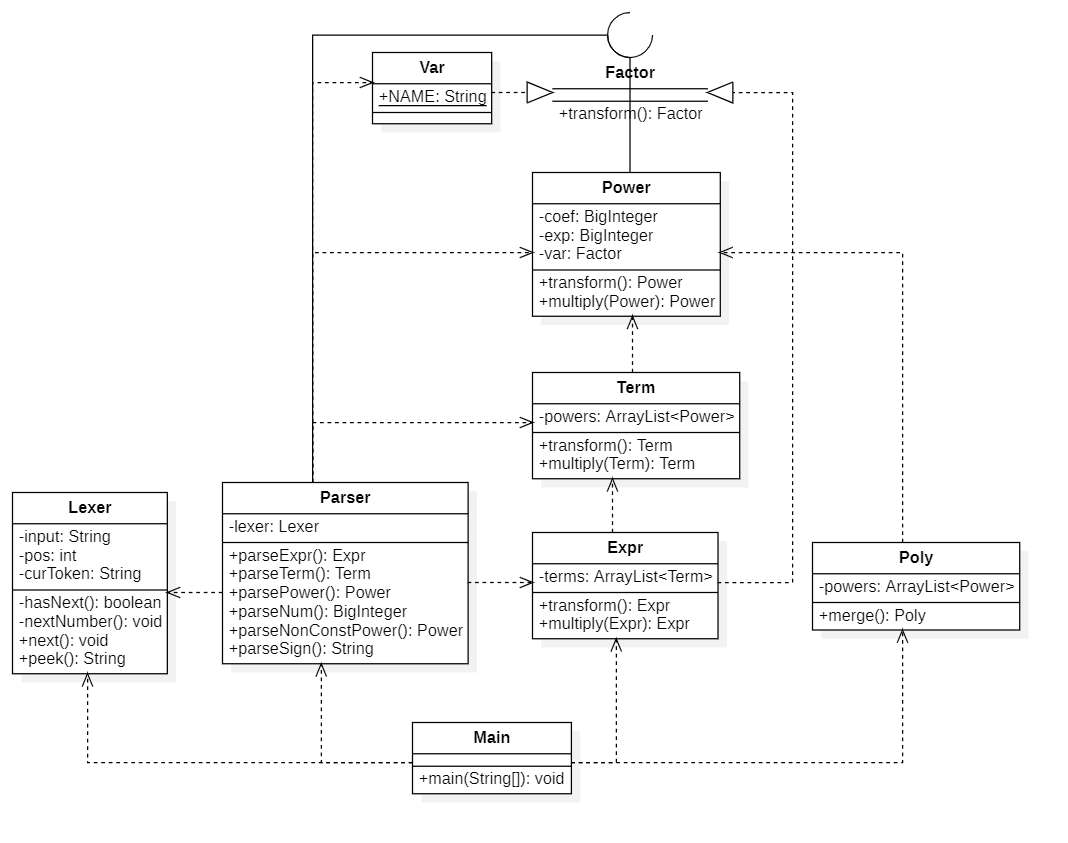
架构分析

• 主体分为解析、化简、合并三个过程，三者之间基本解耦
• 优化在合并过程中完成
• 支持括号嵌套

解析

• 核心类：Parser, Lexer
• 采用递归下降法解析表达式，后续两次作业在此基础上进行迭代
• Lexer 处理输入字符串，一次可取出一个整数或一个其他字符
• Parser 依据表达式树的结构进行解析，生成表达式树之后不再对字符串进行操作

化简

• 核心类：Expr, Term, Power, Factor, Var
• 核心类均为不可变类，化简时会另外生成一个新的对象，不改变原有对象结构
• 自下往上化简，减少表达式树深度，最终得到嵌套层度为 0 的表达式（未合并同类项），例如 1+1*x+1*x+1*x**2
• 表达式树的结构与官方的形式化表述在因子层级不同，笔者将幂函数 Power 作为项 Term 的组成部分，变量 Var 和表达式 Expr 实现接口 Factor 并作为幂函数的底数
• 与官方形式化表述的对应关系：
  • ( Var ) ** 0 <==> 常数因子
  • ( Var ) ** <非0指数> <==> 幂函数因子
  • ( Expr ) ** <指数> <==> 表达式因子

合并

• 核心类：Poly, Power
• 利用 HashMap<BigInteger, BigInteger> 进行合并同类项，key 为幂函数的指数，value 为幂函数的系数

优化

• 系数优化

  • 1*x => x
  • -1*x => -x

• 指数优化

  • x**0 => 1
  • x**1 => x
  • x**2 => x*x

• 正项提前

  • -1+x => x-1

基于度量的分析

代码规模分析

• 总行数小于 500 行，代码规模不大
• 类行数均小于 100 行，功能相对分散

方法复杂度分析

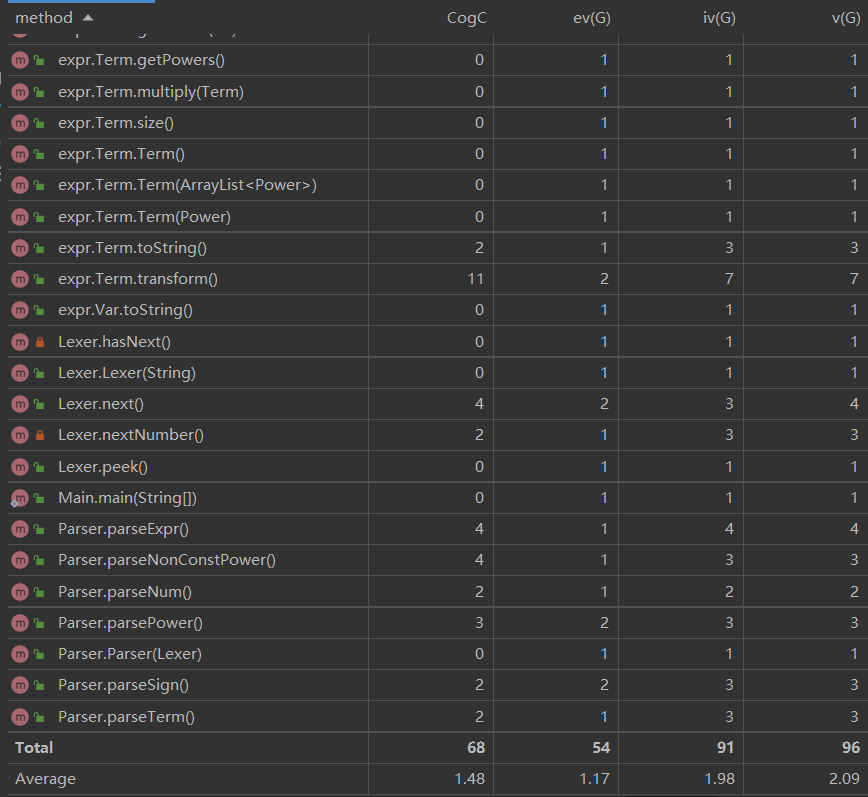
• 平均复杂度不高，方法间耦合度低
• 复杂的较大的方法主要是项的化简以及表达式的字符串化函数

类复杂度分析

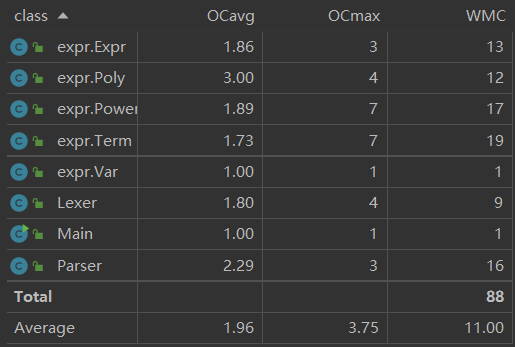
• 平均循环复杂度不高，Poly 在合并同类项以及输出优化时进行过多次循环，因此复杂度相对较高

测试数据

随机数据

• 生成方法：表达式逆解析， 以随机表达式为例：

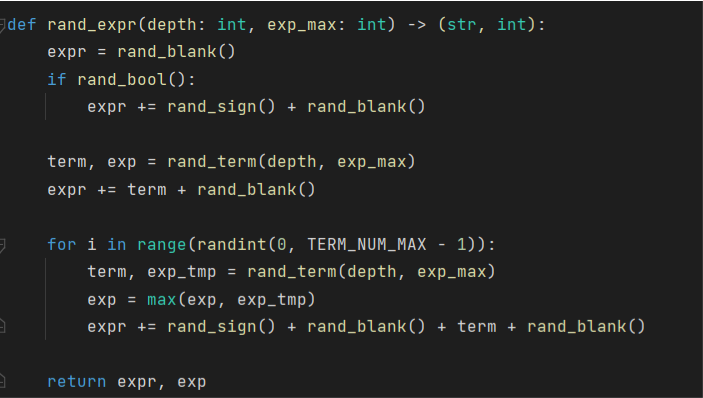
• 范围限制

  • 最大项数
  • 最大因子数
  • 括号嵌套数：官方测试数据不允许括号嵌套，但在本地测试时可以允许
  • 最大指数：不超过 8
    • exp( expr ) = max{ exp( term ) }
    • exp( term ) = sum{ exp( power ) }

常量池数据

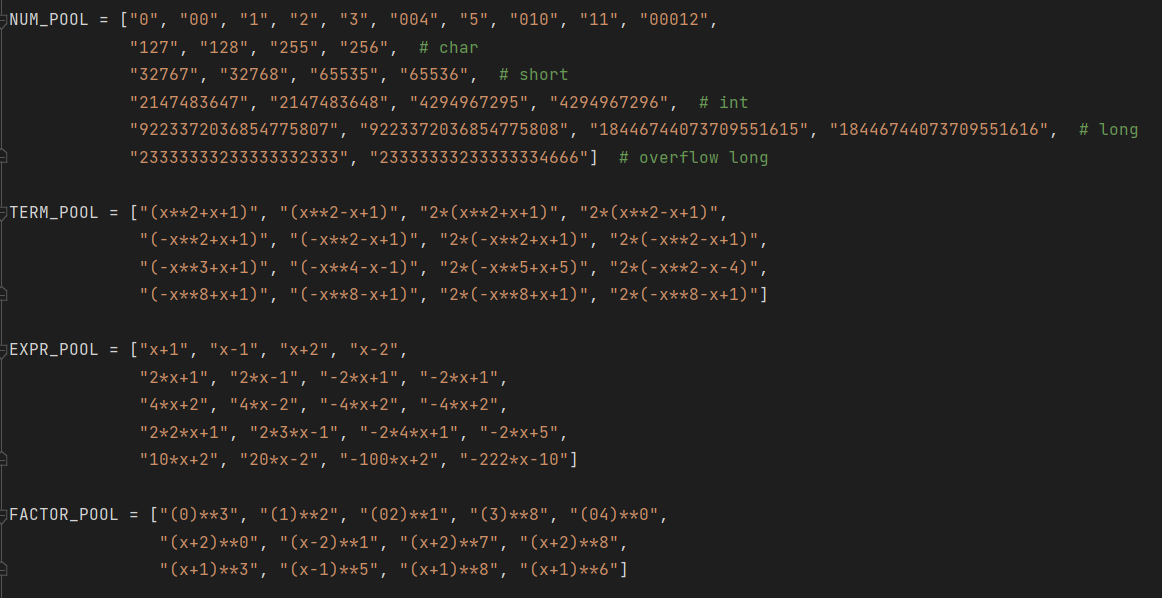
• 在各个层级将随机生成改为从常量池中选取
• 介于随机数据和特殊数据之间，属于半随机数据

特殊数据

• 整数溢出：(9999999999999999999999999)**8
• 指数上限：(x+x+x+x+x+x+x+x)**8
• 全 0 数据：0+0*(0*0*0+0*0*0)*(0)**0+0*0*(0)**0

第二次作业

核心类图

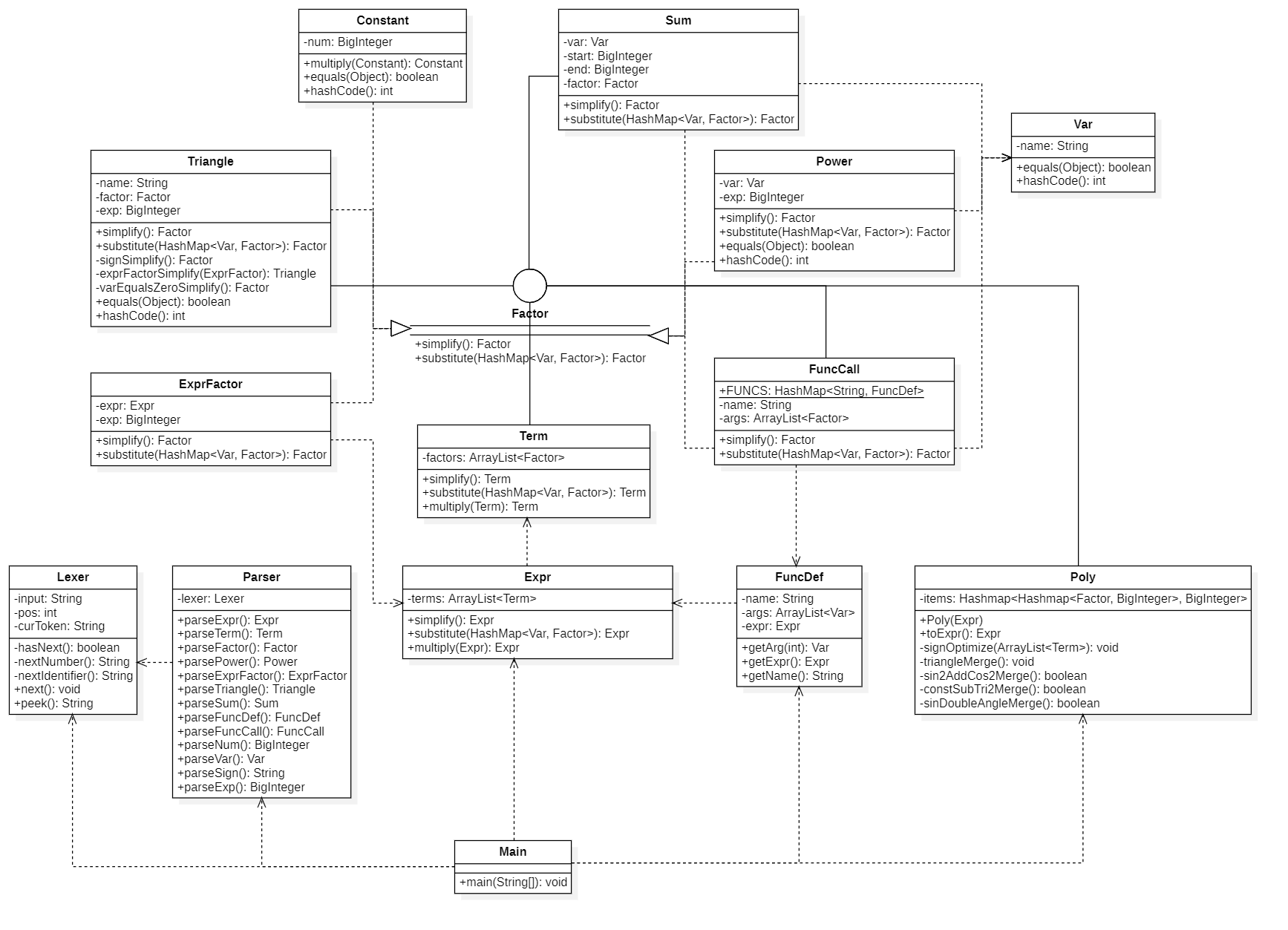
架构分析

• 主体分为解析、化简、合并三个过程，三者之间基本解耦
• 优化在化简和合并过程中完成
• 支持因子嵌套和函数嵌套调用，可直接作为第三次作业

解析

• 核心类：Parser, Lexer
• Lexer 新增 nextIdentifier 方法，一次读出一个标识符，用于获取变量、函数名称
• Parser 根据此次作业表达式树的结构进行了部分重构与迭代

化简

• 核心类：Expr, Term, Factor, Constant, Power, ExprFactor, Triangle, Sum, FuncCall, FuncDef, Var
• 相较于上次作业，在因子层级进行了重构，与官方形式化表述完全一致
• Factor 接口
  • simplify 方法：返回类型不一定与原类型相同，例如 Power 类对象 x**0 在化简后可以返回 Constant 类对象 1
  • substitute 方法
    • 用于进行函数参数带入，将 Var 对象替换成 Factor 对象
    • 只有在 Power 层级才进行带入，其他层级则继续向下传递或停止

合并

• 核心类：Poly, Factor
• 重构 Poly 类，利用 HashMap<Factor, BigInteger> 存储项，HashMap<HashMap<Factor, BigInteger>, BigInteger> 存储表达式
• x*x*sin(2) + 3*cos(1) => HashMap{ <HashMap{ <x, 2>, <sin(2), 1> }, 1>, <HashMap{ <cos(1), 1> }, 3> }

优化

• 相较于上次作业，新增三角函数相关的各种优化（因为数据限制，部分优化到第三次作业才起作用）

• 符号优化

  • sin((-x)) => -sin(x)
  • cos(-1) => cos(1)

• 括号嵌套优化

  • sin((2)) => sin(2)
  • sin((1*x*x)) => sin(x**2)

• 公式优化

  • cos(x)**2 + sin(x)**2 => 1
  • 1 - sin(x)**2 => cos(x)**2
  • 2*sin(1)*cos(1) => sin(2)

基于度量的分析

代码规模分析

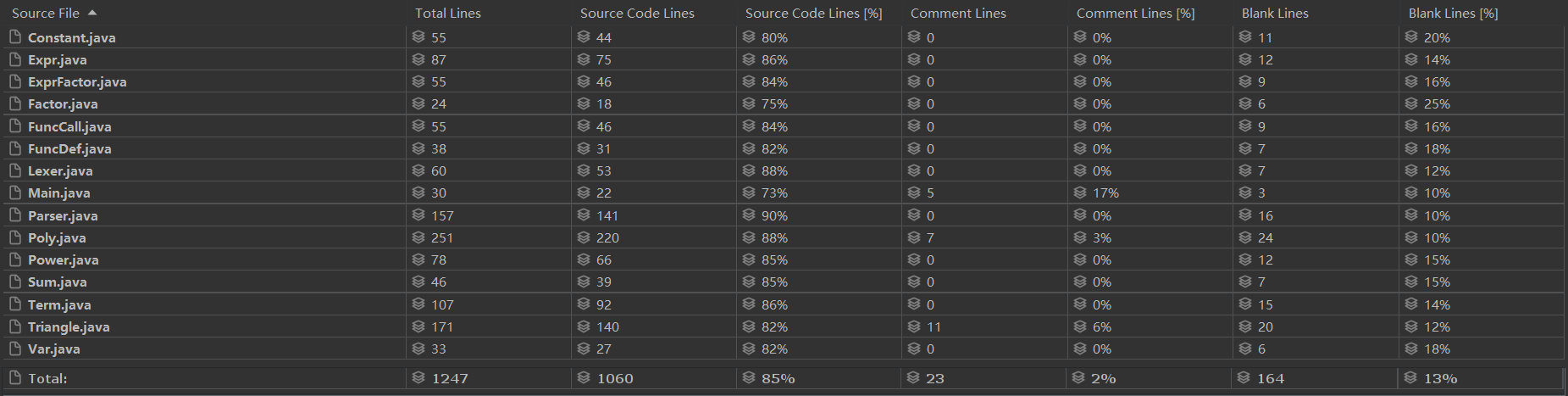
• Poly 类和 Triangle 类行数较多，因为优化主要在这两个类里完成，所需代码量较大

方法复杂度分析

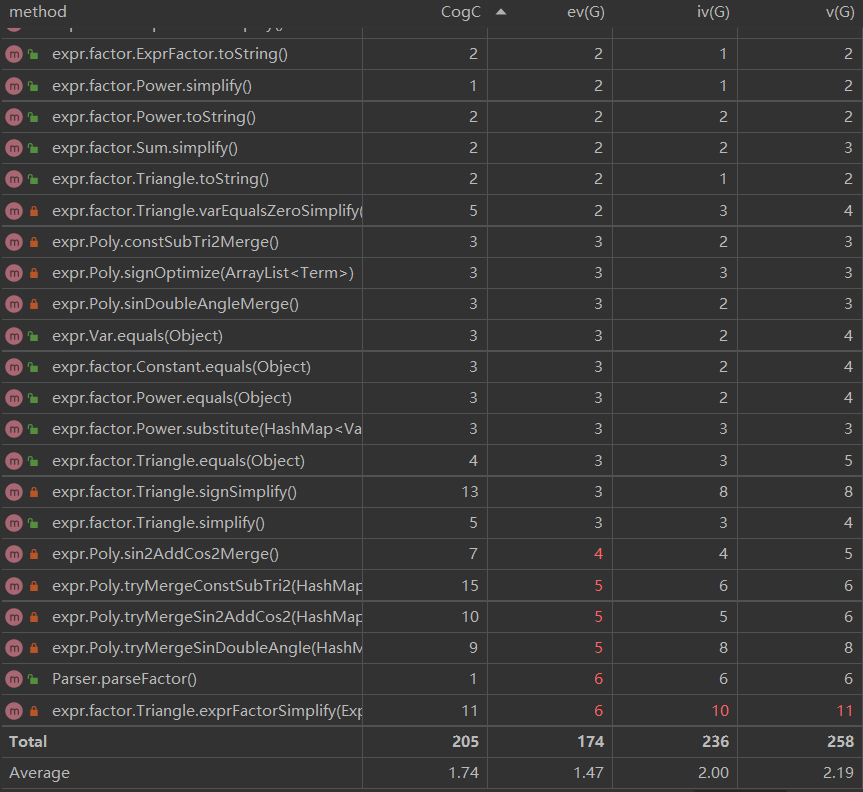
• 平均复杂度不高，耦合度较低
• 复杂度较大的几个方法均是用于优化的，条件判断与循环结构较多

类复杂度分析

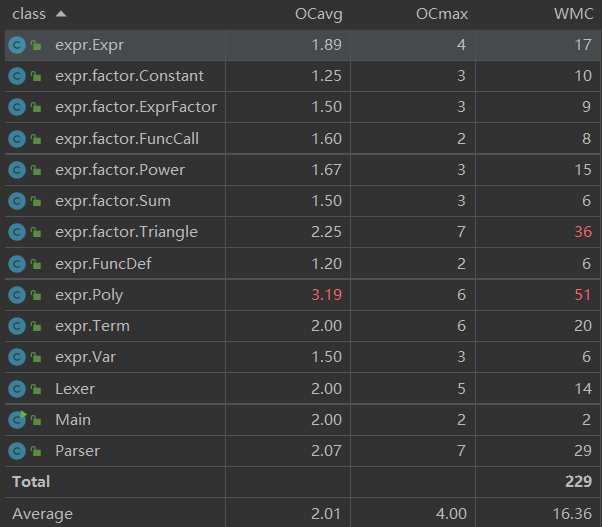
• Poly 与 Triangle 包含大量优化方法，循环结构较多，复杂度较高

数据生成

随机数据

• 进行了简单迭代，增加了新出现的一些因子，新增了规则限制
• 规则限制
  • 可使用的变量
    • 自定义函数定义：x, y, z
    • 主表达式：x
    • 求和函数：已知的可使用变量 + i
  • 禁止函数调用
    • 自定义函数定义和求和函数
    • 自定义函数调用（第三次作业允许）

常量池数据

• 新增三角函数池

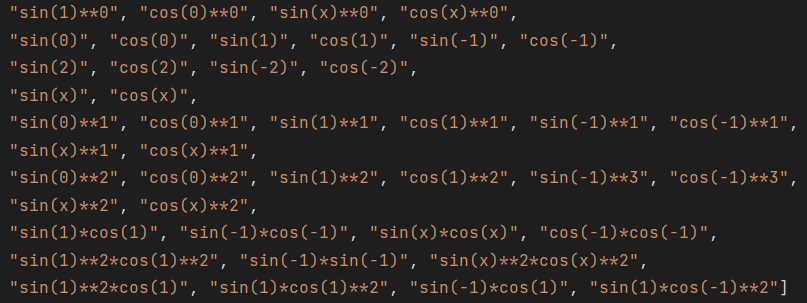
特殊数据

• 针对本次作业规则以及自己的优化过程，新增了一些手动构造的数据
• 括号嵌套：sin(((f(g(f(h(-1))))))), 其中f(x) = g(x) = h(x) = (x)
• 三角化简：
  • 符号化简：sin(-1)**2, cos(-1)**2, sin((-x-1))
  • sin2 + cos2 = 1：cos(x)**2+sin(x)**4+cos(x)**2*sin(x)**2
  • 1 - sin2 = cos2：sin(x)**2*cos(x)**2-sin(x)**2
  • sin 二倍角公式：-3*2*sin(1)**2*cos(1)**2

第三次作业

核心类图

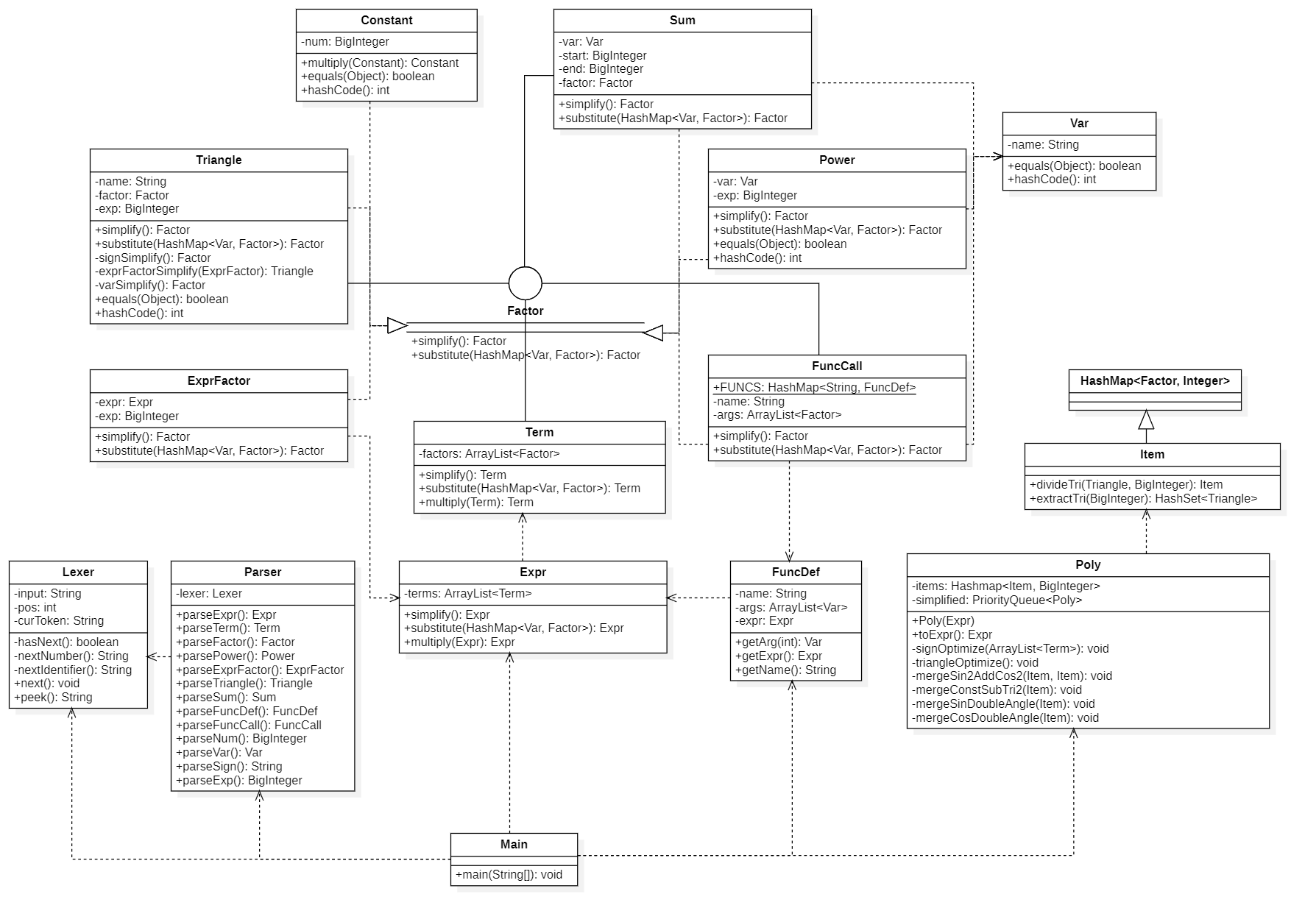
架构分析

• 主体分为解析、化简、合并三个过程，三者之间基本解耦
• 优化在化简和合并过程中完成

解析

• 较上次作业没有变化

化简

• 较上次作业没有变化

合并

• 核心类：Poly, Item, Factor
• Item 类
  • 继承自 HashMap<Factor, BigInteger> 类
  • 主要目的是为了缩短类名，并增加两个方法用于三角函数优化，使用更加方便

优化

• 新增公式优化：1 - 2*sin(1)**2 => cos(2)
• 公式优化策略
  • 贪心算法
  • 利用优先队列 PriorityQueue<Poly>，按字符串长度排序
  • 每一轮尝试所有可能的公式变形，生成新的 Poly 对象扔进优先队列。结束后取出队首元素，若该表达式长度小于原本表达式，则进行替换，并继续化简；否则结束化简。

基于度量的分析

代码规模分析

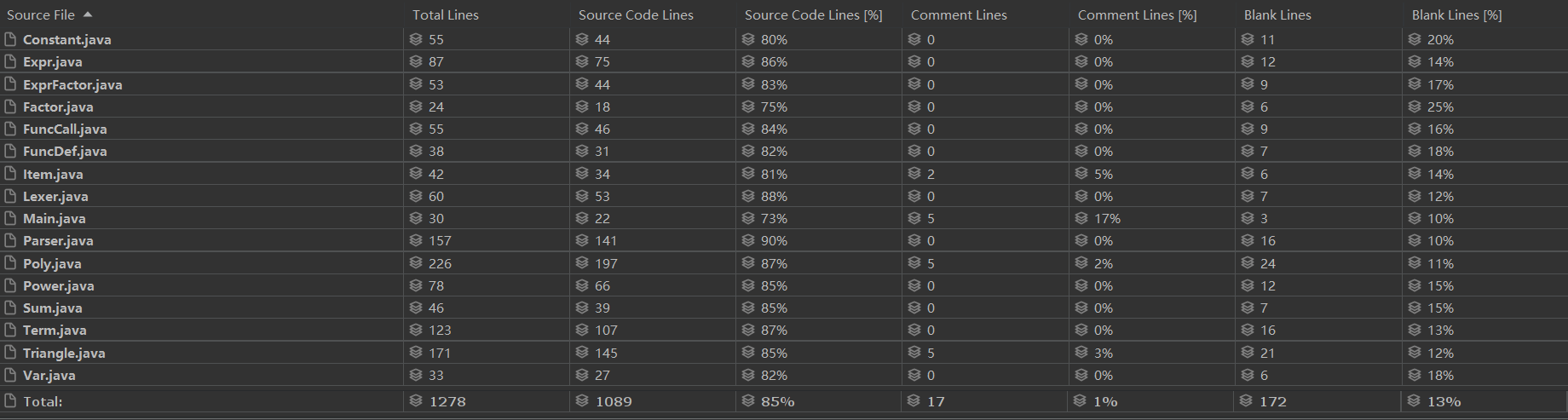
• 由于第二次作业已满足本次作业要求，所以并未有太大改动，代码行数基本不变

方法复杂度分析

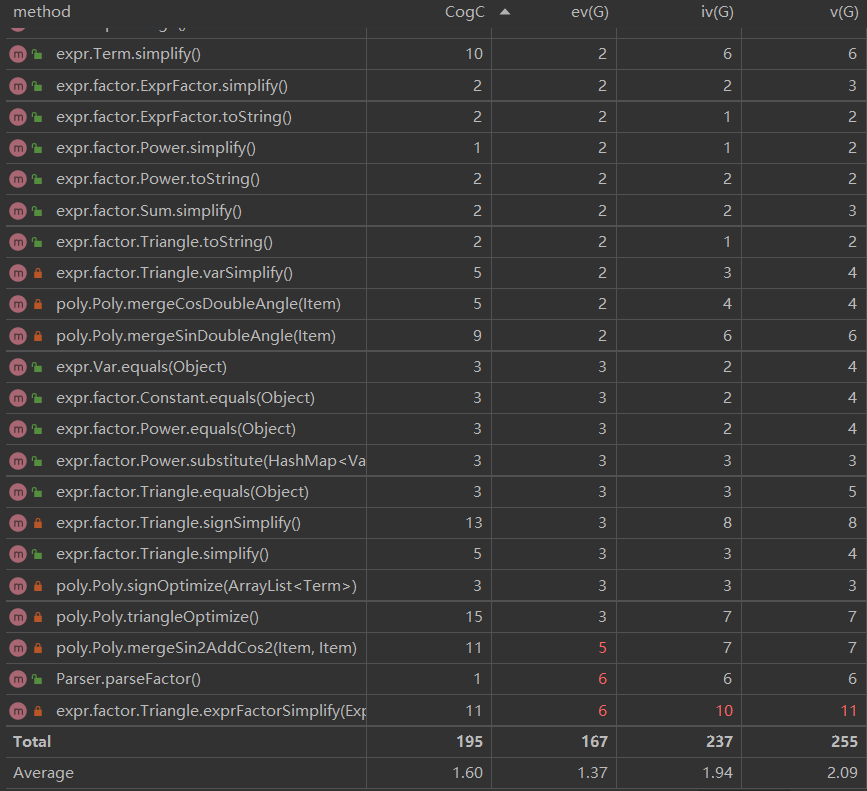
• 对优化方法做了一些改动和优化，所以复杂度略有下降
• 复杂度较大的方法仍集中在优化部分

类复杂度分析

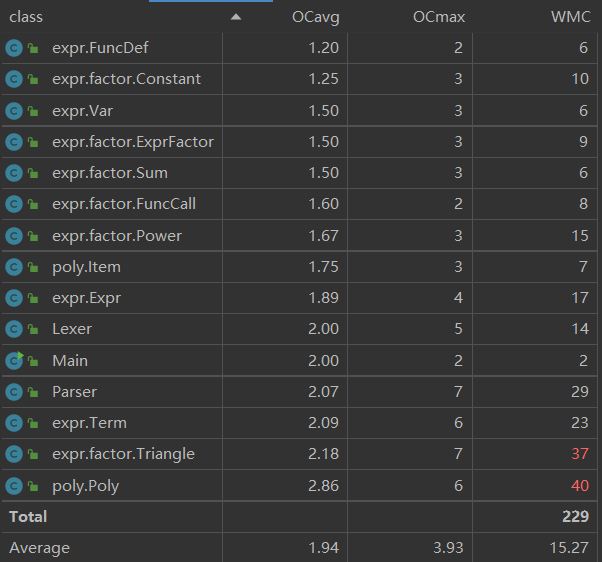
• 引入的 Item 类分担了原本 Poly 类的部分功能，使 Poly 复杂度有所下降
• 各项平均复杂度也均有降低

数据生成

随机数据

• 较上次作业没有太大改动

常量池数据

• 较上次作业没有太大改动

特殊数据

• 针对新增的优化方法以及并未实现的优化方法构造了一些数据
• cos 二倍角公式：2*cos(x)**2*cos((2*x))+sin((2*x))**2+cos((2*x))
• 和差角公式：2*cos(x)**2*cos((2*x))+sin((2*x))**2+cos((2*x))

测试策略与bug分析

测试策略

基本流程

• 主要采用黑盒测试 + 随机轰炸
• 自动测试：命令行编译、运行，使用 subprocess 模块
• 正确性检查：利用 sympy 库
• 格式检查：利用正则表达式

对拍测试

• 本地三人对拍，用于检测自己程序的正确性
• 可同时检测三个人的 bug，并且三个人同时跑的话效率能高 3 倍

多人测试

• 用于互测，以自己的程序为标准与其他人对拍
• 利用循环结构进行串行测试

数据分析

• 通过数据拆解或答案比对，构造出引起错误的极小项
• 随后调整数据生成器或者修复他人bug
• 避免不断 hack 同质 bug，增加 hack 效率

本人bug

• 三次强测和互测中均未发现 bug
• 本地测试中遇到过的一些问题
  • 参数代入问题
    • 数据：0 f(y, x) = x*sin(y) f(x, 1)
    • 原因：原本 substitude 方法的参数表是 (Var, Factor)，一次只能代入一个参数。因此会先代入 y=x，得到 x*sin(x)，再代入 x=1，得到 sin(1)，与答案 sin(x) 不符
    • 解决办法：修改参数表为 (HashMap<Var, Factor>)，同时传入所有要代入的参数。并且能提升效率（只遍历一遍表达式树，原本可能遍历 1 ~ 3 遍）
  • 优化后变长
    • 数据：-3*2*sin(x)**2*cos(x)**2
    • 原因：不进行二倍角优化，结果是 -6*sin(x)**2*cos(x)**2；进行二倍角优化，结果是 -3*sin((2*x))*sin(x)*cos(x)，答案更长
    • 解决办法：引入优先队列 PriorityQueue 来存储优化的结果，并与原表达式进行长度比较

他人bug

• 第一次作业：hack 1 人 1 个 bug
• 第二次作业：hack 4 人 8 个 bug
• 第三次作业：hack 3 人 6 个 bug
• 完全采用黑盒测试，并未根据他人代码构造针对性样例
• 根据公开的hack结果，只有第三次作业的一个点并未hack到，原因是没有进行严格的格式检查；总体来说测试数据的强度还可以，覆盖率较高，并没有出现因数据问题而没有hack到的情况

反思总结

迭代与重构

• 第一次作业到第二次作业迭代的工作量较大，主要原因有三
  • 在因子层级进行了重构
  • 新增了较多因子，代码量翻倍
  • 做三角函数优化花了不少时间
• 第二次作业到第三次作业几乎没有进行什么修改
  • 第二次作业已经能满足第三次的要求
  • 增加了一点三角函数优化
  • 修改了优化部分的代码，复杂度更低

架构的优缺点

优点

• 代码逻辑清晰，不同功能类之间的耦合度较低
• 对于表达式树的维护较好，具有较强的鲁棒性、可扩展性

缺点

• 优化部分算法简单，效率较低，很多情况无法得到最优解
• 在表达式树的设计中没有引入运算符层级，如果新增除法或其他运算符，可能会需要不小的重构

心得体会

• 提升了面向对象思维能力和层次化设计能力
• 学会了递归下降法解析表达式
• 对于设计模式有了一定了解
• 数据构造和自动化测试水平提高