基于布尔运算的多边形裁剪算法

最近因为业务需求，研究了一下 Francisco Martínez 的多边形裁剪算法，遂在此记录下学习。

 

标签: 2D, 多边形裁剪, 布尔运算, 计算机图形学

---

前言

　　2D 多边形裁剪在图形学中比较常见，尤其在计算机辅助制图、GIS 领域有着广泛的应用场景。本文所介绍的算法，目的是实现：给任意两个多边形顶点序列（无论按照顺时钟还是逆时钟顺序），计算出两多边形的交集、差集（A - B 以及 A ⋃ B - A ⋂ B）、并集，并保持计算结果的拓扑关系，借鉴原文之图如下图所示：

 

 

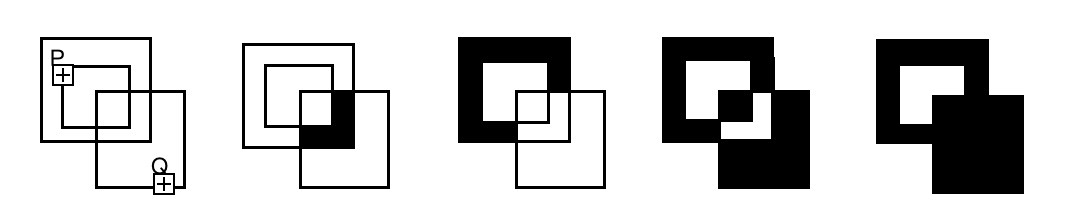
使用该算法条件：1. ✅ 多边形可以包含子多边形; 2. ❌ 但同一多边形不允许两条边重叠。

　　

　　本文的技术路线将先从两线段求交开始，因为这部分是基础算法，可以独立出来。接着介绍拓扑关系理论知识，并给出一案例让读者大致了解作者的意图。有了前置知识后，笔者将按照对边进行空间排序、根据边空间关系计算边的拓扑属性、用扫描线算法对相交的边做裁剪、根据布尔操作，选择裁剪后具有相应拓扑属性的边作为区域的边界这个顺序来进行阐述。

　　

　　算法处理的多边形是两组，将其中一组定义为被裁剪对象或 Subject 类型，另一组是裁剪对象或 Clipping 类型，用 Clipping 类型的多边形去裁剪 Subject 类型的多边形。

两线段求交

　　计算两多边形交差并，最终都将归结于最小图元的计算，即线段求交。与求两直线交点不同，由于线段有长度，如果经过深入思考的话，情况并没有想象的那样简单。比如求两多边形相交的区域，需要考虑两多边形的某条边有重叠，那么重叠的线段应当被计算出来作为相交区域的边界，而通常跨立实验并没有考虑这样的情况。这里给出两线段之间的位置关系，如下图所示：

　　

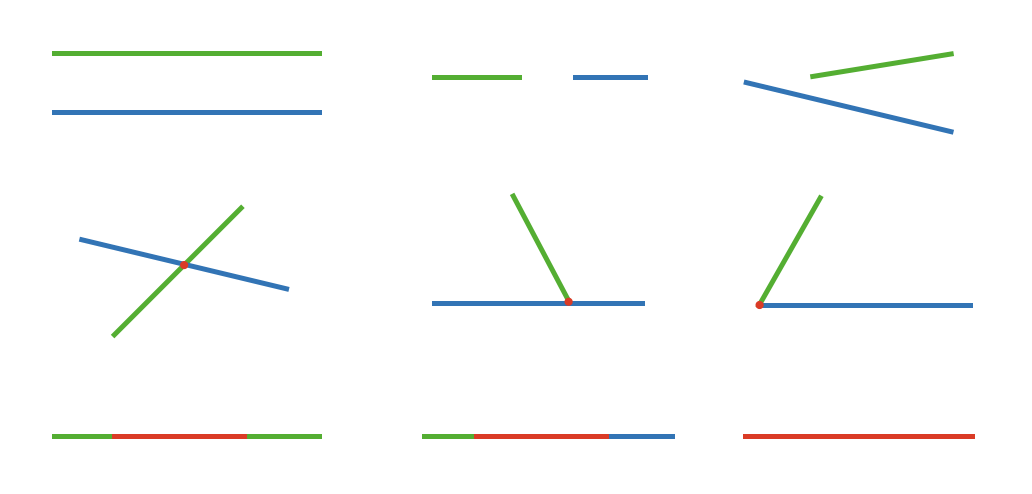
　　图中红色标注为两线段相交部分。为计算相交部分，我们将线段表示为 start -> end 的向量，通过向量的叉积和点积运算来判断线段的位置关系并计算出相交部分。在计算之前，需要对数据做些处理，如果某线段两点过于接近甚至重合，我们视该线段为一点，在刚开始输入多边形数据的时候，剔除其中的一个端点，这样保证所给的线段都有长度。于是给出任意两线段 segment1(start, end)、segment2(start, end)，算法计算结果为 n，p1，p2（对于相交于一点的情况，n = 1，p2 没有意义；对于两线段有重叠的情况，n = 2，p1，p2 从左至右分别表示重叠部分的端点，可能这样表达并不准确，比如垂直情况，那么 p1，p2 应该分别表示在 segment1 的 start -> end 方向上重叠部分的左端点和右端点），算法如下：

 

input:s1(start, end), s2(start, end) // 输入两线段
output: n, point1, point2 // 计算结果
begin
    vector v1, v2;
    vector v3 = (s2.start.x - s1.start.x, s2.start.y - s1.start.y); // 计算s1.start -> s2.start的向量
    double crossV1V2, sqrCross = crossV1V2 * crossV1V2; // v1, v2叉乘及叉乘平方
    if (sqrCross > .000001 * sqrLen1 * sqrLen2) { // sqrLen1、sqrLen2分别为v1、v2模长的平方，且sqrLen1 > 0, sqrLen2 > 0，此判断v1、v2不共线
        // s、t都满足如下条件时，v1、v2才相交，<font color=red>具体分析参见下图</font>
        double s = crossV3V1 / crossV1V2;
        if (s < 0 || s > 1) return n = 0;
        double t = crossV3V2 / crossV1V2;
        if (t < 0 || t > 1) return n = 0;
        point1 = (s1.start.x + v1.x * s, s1.start.y + v1.y * s);
        // 若point1接近端点，则端点赋予point1
        if (distance(point1, s1.start) < .000001) point1 = s1.start;
        ...
        return n = 1;
    }
    // 以下讨论共线情况

    // 两线段不在一条线上
    double sqrLen3, sqrCrossV3V1;
    if (sqrCrossV3V1 > .000001 * sqrLen3 * sqrLen1) return n = 0; // v3、v1不共线 -> v1, v2平行但不在一条线上

    // 两线段在一条线上, v1、v2、v3两两之间要么为0度要么为180度
    // 计算重叠部分
    double s0 = dot(v3, v1) / sqrLen1;
    double s1 = s0 + dot(v1, v2) / sqrLen1;
    s0 = min(s0, s1), s1 = max(s0, s1);
    double w[2] = [-1, -1]; // w存储重叠部分在v1上的起点位置和终点位置, [0, 1]区间
    if (s0 > 1 || s1 < 0) return n = 0; // 同一条线上但不重叠
    if (s0 < 1) {
        if (s1 > 0) {
            s0 > 0 ? w[0] = s0 : w[0] = 0;
            s1 < 1 ? w[1] = s1 : w[0] = 1;
        } else {
            w[0] = 0;
        }
    } else {
         w[0] = 1;
    }
    point1 = (s1.start.x + v1.x * w[0], s1.start.y + v1.y * w[0]);
    // 若point1接近端点，则端点赋予point1
    if (distance(point1, s1.start) < .000001) point1 = s1.start;
    ...
    if (w[1] != -1) {
        point2 = (s1.start.x + v1.x * w[1], s1.start.y + v1.y * w[1]);
        return n = 2;
    }
    return n = 1;

　　

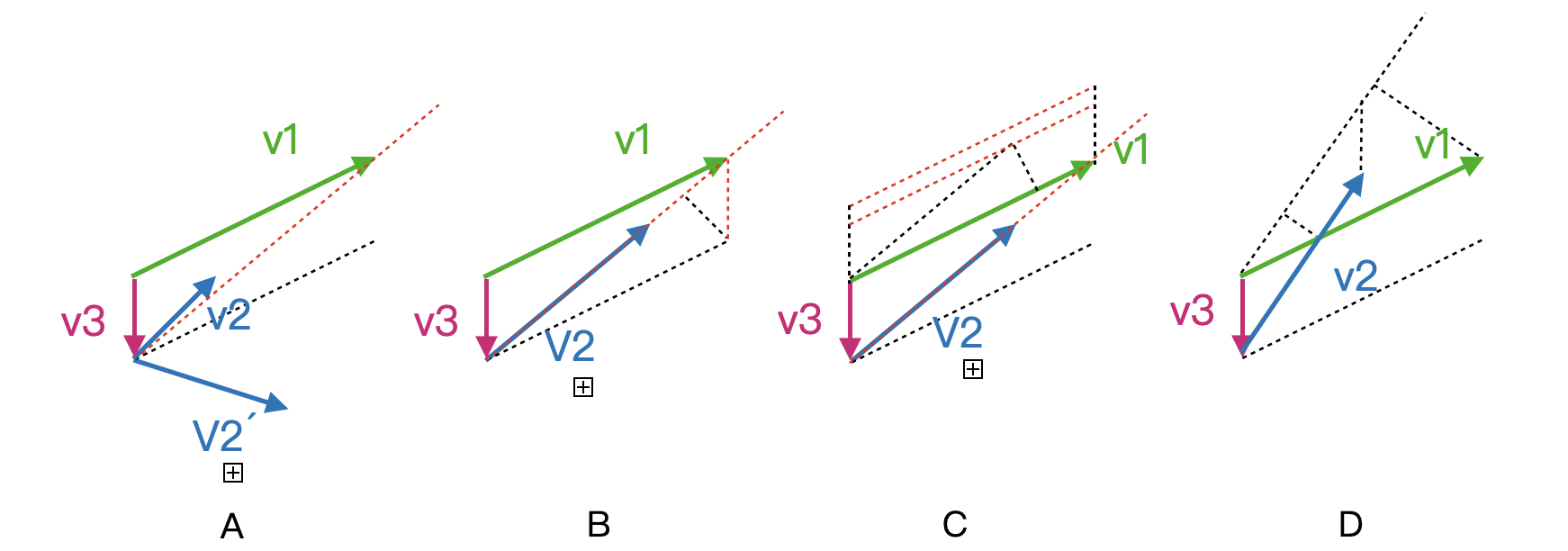
　　在两线段不共线的情况下，判断两线段是否相交除了有跨立实验，还有本文所用方法，如下图 A 所示，v3 为 v1 起点到 v2 起点的向量，如果 v1、v2 相交，则 v2 必须要穿过 v1、v3 所在直线和红色虚线所围成的区域。而且只有当 v2 落在 v1、v3 所在直线和黑色虚线所围区域或穿过该区域，v3 x v1、v3 x v2 以及 v1 x v2 的结果才能保证同号，否则如 v1 x v2´ 与 v3 x v1 那样一负一正。进一步，判断 v2 是否穿过边届为红色虚线的那个区域（包括 v2 终点落在 v1 上），则需要保证:

　　ⅰ. v3 到 v1 的垂线长度 / v2 到 v1 的垂线长度 <= 1;

　　ⅱ. v3 到 v2 的垂线长度 / v1 到 v2 的垂线长度 <= 1。

　　图 B 中的 v1，v2，v3 虽然满足了 ⅱ 条件，v1，v3 到 v2 的垂线长度相等，但在图 C 中不满足 ⅰ 条件。当以上都满足时，如图 D 所示，根据相似三角形原理，由已知条件 v1 起点，v1 向量以及垂线长度比可求出交点。

拓扑关系

　　拓扑关系主要用来描述图形元素之间的位置关系，是这个算法的核心思想。它影响：① 边的处理顺序（边排序）；② 对边裁剪后如何在边集合中选择边作为并集、交集、差集区域的边界；③ 保持多边形之间的包含关系，小多边形被包含于大多边形中，也就洞。这三点也是我们后面一直讨论的内容，首先我们按原文内容做如下推理：我们先做一个约定：不考虑多边形与多边形相交。那么经过多边形的左下角端点做出一条向下的射线，如下图 A 所示， 我们的观察方向是沿这条射线从下往上看。

　　

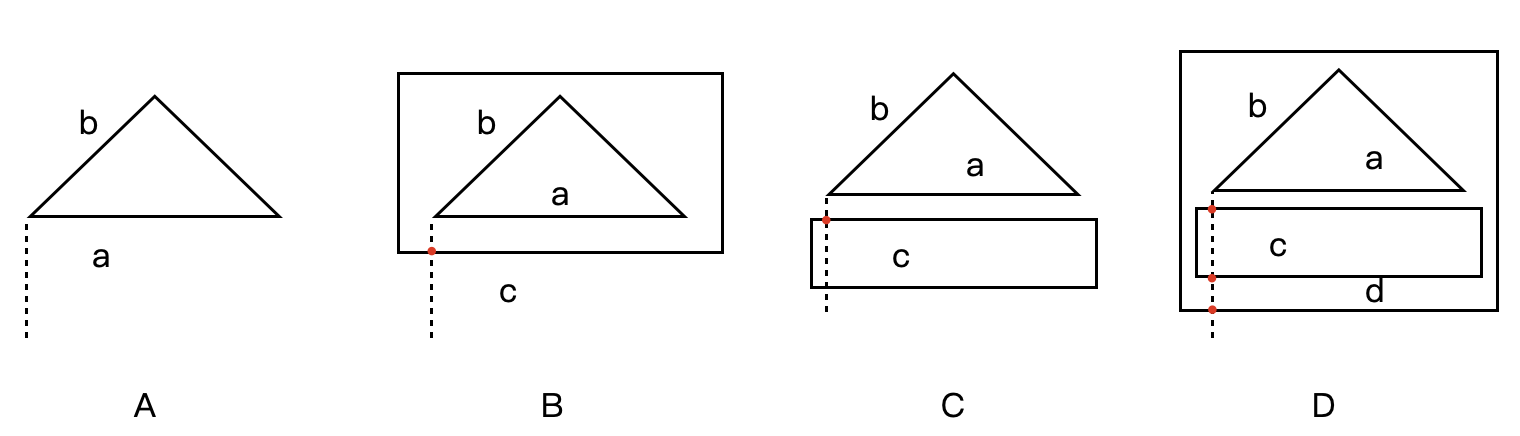
　　1. 让我们来看图 A，对于 a 这条边，射线是从外面向里面过渡的（outside -> inside），对 b 这条边来说，则是从里面向外面过渡（inside -> outside），不存在 “离 a 最近、不属于同一多边形的边” 与射线相交，那么我们认定该多边形就是一个外多边形（外轮廓）。

　　2. 让我们来看图 B，射线与 "离 a 最近的、不属于同一多边形的边" 有一个交点，这个点在 c 上，对 c 这条边来说，射线是从外面向里面过渡的（outside -> inside），让我们根据前面描述，对 a、c 都是 outside -> inside，那么说明三角形在最外层多边形的内部。

　　3. 让我们来图 C，射线与 "离 a 最近、不属于同一多边形的边" 有一个交点，这个交点在 c 上，对 c 这条边来说，射线是从里面向外面过渡的（inside -> outside）, 对 a 是 outside -> inside，则说明这两个多边形都在彼此的外侧。

　　4. 让我们再来看图 D，射线与 "离 c 底边最近且不属于同一多边形的边" 有一个交点，这个交点在 d 上，对 d 这条边来说，射线是从外面向里面过渡的（outside -> inside），这说明外部轮廓包含内部矩形，并且根据我们在图 C 的讨论，三角形和矩形互不包含，那么说外部轮廓也包含内部三角形，三角形和内部矩形属于并列关系。

　　

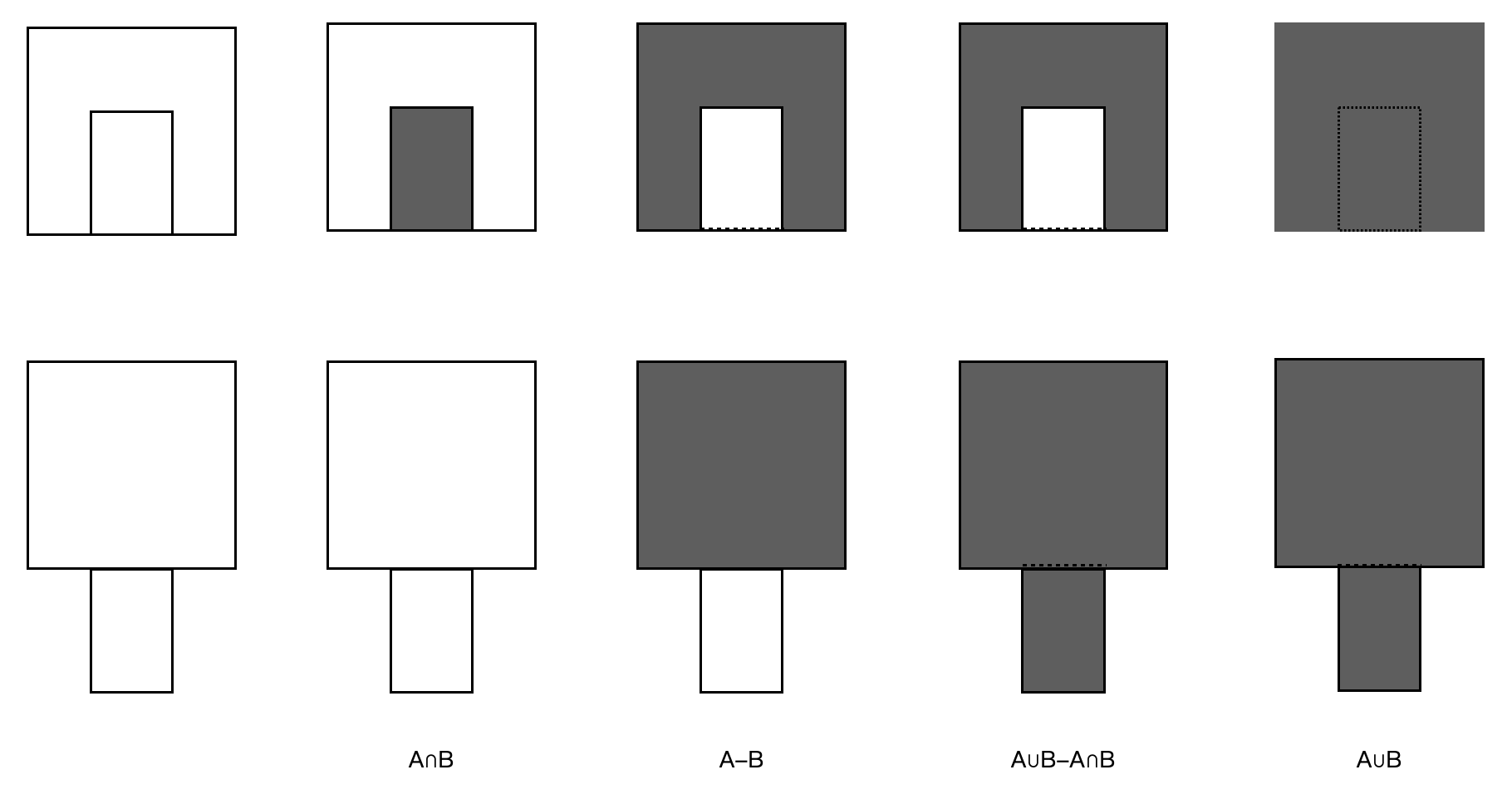
　　在这里做进一步讨论，我们为每条边赋予一个布尔属性，与源码保持一致，我们的字段名为 inOut，true 表示 inside -> outside，根据上面的论述，我们再为每条边赋予另一个布尔属性：otherInOut，这个属性记录 在这条边的下面、离这条边最近且不属于同一多边形的边 是否是 inside -> outside。这里我们直接给出上图各边属性的计算结果，让读者先大致了解作者的意图，如下图所示，F， T 表示 inOut: false, otherInOut: true。其中图 A 和图 C 的属性计算是没有意义的，因为在最开始，作者会做包围盒（bounding box）判断，如果只输入一个多边形或者两个多边形的包围盒不相交，那直接返回结果，不会有接下来计算属性的流程，笔者在这只是顺手标记了而已。

　　

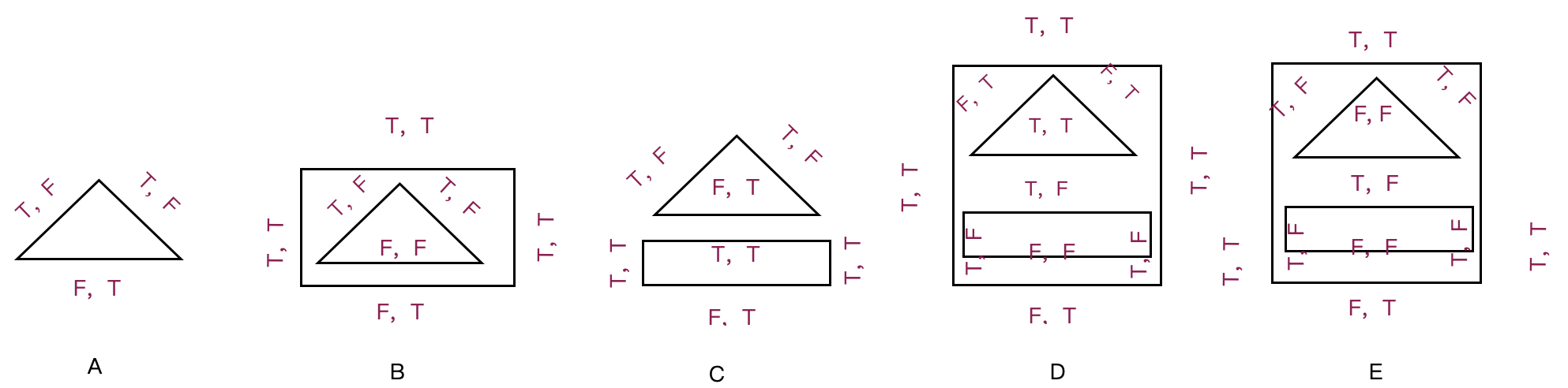
　　1. 对图 A：假设三角形是被裁剪对象 A ⋂ B 结果为空，A ⋃ B 还是三角形，A ⋃ B - A ⋂ B 根据前面结果还是三角形，A - B 作者定义为空，读者根据需求自行决定。假设三角形是裁剪对象，作者定义 A ⋃ B、A ⋃ B - A ⋂ B 是三角形，其他都为空。

　　2. 对图 C：假设三角形是被裁剪对象，矩形是裁剪对象。A ⋂ B 为空，A - B 为三角形，A ⋃ B、A ⋃ B - A ⋂ B 的结果都为 A ⋃ B。

 

接下来讨论包围盒有重叠的情况，就需要 otherInOut 这个属性了，在图中表示的就是边的第二个属性值：

 

　　3. 对图 B：笔者是定义矩形为被裁剪对象，三角形是裁剪对象。那么 A ⋃ B 就是 otherInOut 为 true 的这些边组成的区域，A ⋂ B 就是 otherInOut 为 false 的这些边组成的区域，A - B 就是被裁剪对象(矩形)的边 otherInOut 属性值为 true，裁剪对象(三角行)的边 otherInOut 属性值为 false 的边集合组成的区域，A ⋃ B - A ⋂ B 就是选择所有边，最终结果是将三角形作为矩形的洞，在这个例子中 A - B 与 A ⋃ B - A ⋂ B 的结果是一样的。

　　4. 对图 D：笔者定义最外层矩形和里面的三角形作为被裁剪对象（属性计算结果给也证明了内部三角形是作为外部矩形的洞这一特性的，因为三角形底边 inOut 为 true），内部矩形为裁剪对象。根据第三点的逻辑，A ⋃ B 就是 otherInOut 为 true 的这些边组成的区域，A ⋂ B 就是 otherInOut 为 false 的这些边组成的区域，A - B 就是被裁剪对象(外部矩形和三角形)的边 otherInOut 属性值为 true，裁剪对象(内部矩形)的边 otherInOut 属性值为 false 的边集合组成的区域，A ⋃ B - A ⋂ B 就是选择所有边，最终结果是将三角形和内部矩形作为外部矩形的洞，在这个例子中 A - B 与 A ⋃ B - A ⋂ B 的结果是一样的。

　　5. 对图 E：笔者定义最外层矩形作为被裁剪对象，内部矩形和三角形作为裁剪对象（属性的计算结果也证明了这一点，三角形和内部矩形的底边 inOut 都为 false），3、4 点的描述同样也适用于此。

　　

　　笔者个人体会：其实程序主要就是在计算这些属性，当考虑复杂的多边形与多边形边相交情况时，也就是对相交的边做裁剪，那么处理后的边也就被看成如上图那样成为不相交区域的边界，换种说法就是经过裁剪后，原来相交的两组复杂多边形区域被细分成更小、被认为不相交的被裁剪区域和裁剪区域，刚才讨论的 3、4、5 点就可以直接运用上了。还要再说一点的就是 otherInOut 的另一层含义就是表示是否为外边界，因此最开始，最靠下的边被赋予 true，属于同一裁剪类型（裁剪 | 被裁剪）的边在传递该属性，如图 B、C、E 那样，以图 B 为例，内部三角形最高顶点所连接的两个边在传递底边 otherInOut 属性，所以在 D 图，内部三角形为 true，他是被裁对象，他对离它最近，不属于同一类型多边形的边的 otherInOut 取反，而在 E 图，因为属于同一类型，所以在传递。

　　这些属性是怎么计算的，垂直的边它在理论上与射线平行，它的 inOut 又是怎么计算的，那么为了快速计算每条边的属性，以及后续对相交的边做裁剪，我们对顶点、边进行排序，重点来了！这是核心的核心！

边裁剪

　　对于每条边，都有左端点和右端点，对边排序主要依据左端点以及边与边的空间位置来的。作者首先定义了这样的数据结构代表每个点，也可以代表每条边，也可以看成一次扫描线事件，根据类名就可以看出来了，扫描事件我们后续在讨论。

struct SweepEvent {
    bool left; // 是否是左端点
    Point2D point; // 端点几何数据
    SweepEvent *otherEvent; // 同一边的另一个端点对应的SweepEvent，同一边的两个端点相互指向
    PolygonType pol; // 所属多边形的类型[SUBJECT(被裁的对象)，CLIPPING(用于裁剪的对象)]，在输入数据时，我们会依次输入被裁多边形与裁剪多边形这两组数据，程序在处理输入数据时候，就为每个点确定了这个类型
    bool inOut; // 如前文描述，是否是inside -> outside
    bool otherInOut; // 如前文描述， 离该边最近且在该边的下面的那条边是否是inside -> outside
    ...
}

　　

　　假设给出如下图的一个多边形数据，在数据处理时候，除了剔除被认为是重复的顶点（线段求交那里做了说明），我们根据顶点数据将得到一系列 SweepEvent 对象。其中值得注意的是左端点的判定：最左边的顶点被认为是左端点，若 x 相同，则最下面的顶点被认为是左端点。

　　

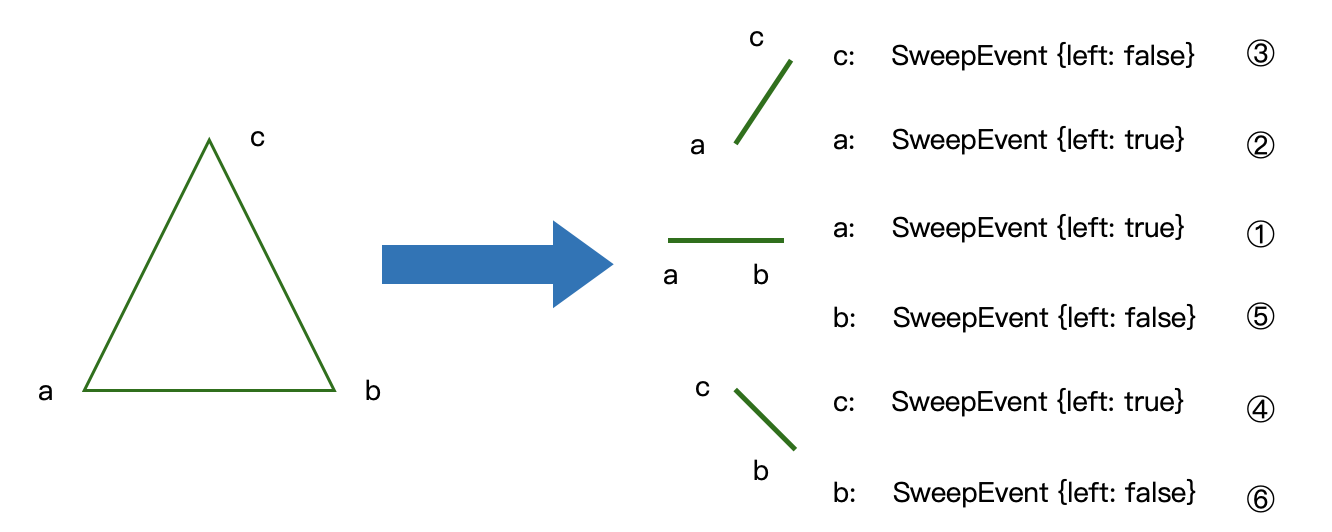
　　两组多边形（裁剪与被裁剪）的 SweepEvent，将统一放在一个小顶堆中，小顶堆每次只保证拿到（pop( )、top( )）的数据最小，相反，每次拿到的数据最大叫大顶堆。那么 SweepEvent 对象在队列中的排序规则定义如下：

　　1. x 越小越靠近堆顶；

　　2. x 相同则 y 越小越靠近堆顶；

　　3. x 与 y 相同，则 right 端点靠近堆顶；

　　4. 两个端点所在的边不共线，则最下面的边对应的端点靠近堆顶；

　　5. 否则按照地址大小排序。

所以才有了如上图右边的排序，图中 a 顶点在最左侧，根据第一条规则，pop 得到的首先是端点对应的 sweepevent 对象，但 a 端点有两个 sweepevent 对象，且 y 相同，都为左端点，所以根据第四条规则，底边在斜边的下方，所以底边的左端点对应的 sweepevent 具有最高优先级，其次是斜边的左端点。后面的以此类推。

　　

　　顶点排序保证了顶点从左到右，同一位置顶点连续，其次是从下到上的排序状态，如下图所示。

 

　　

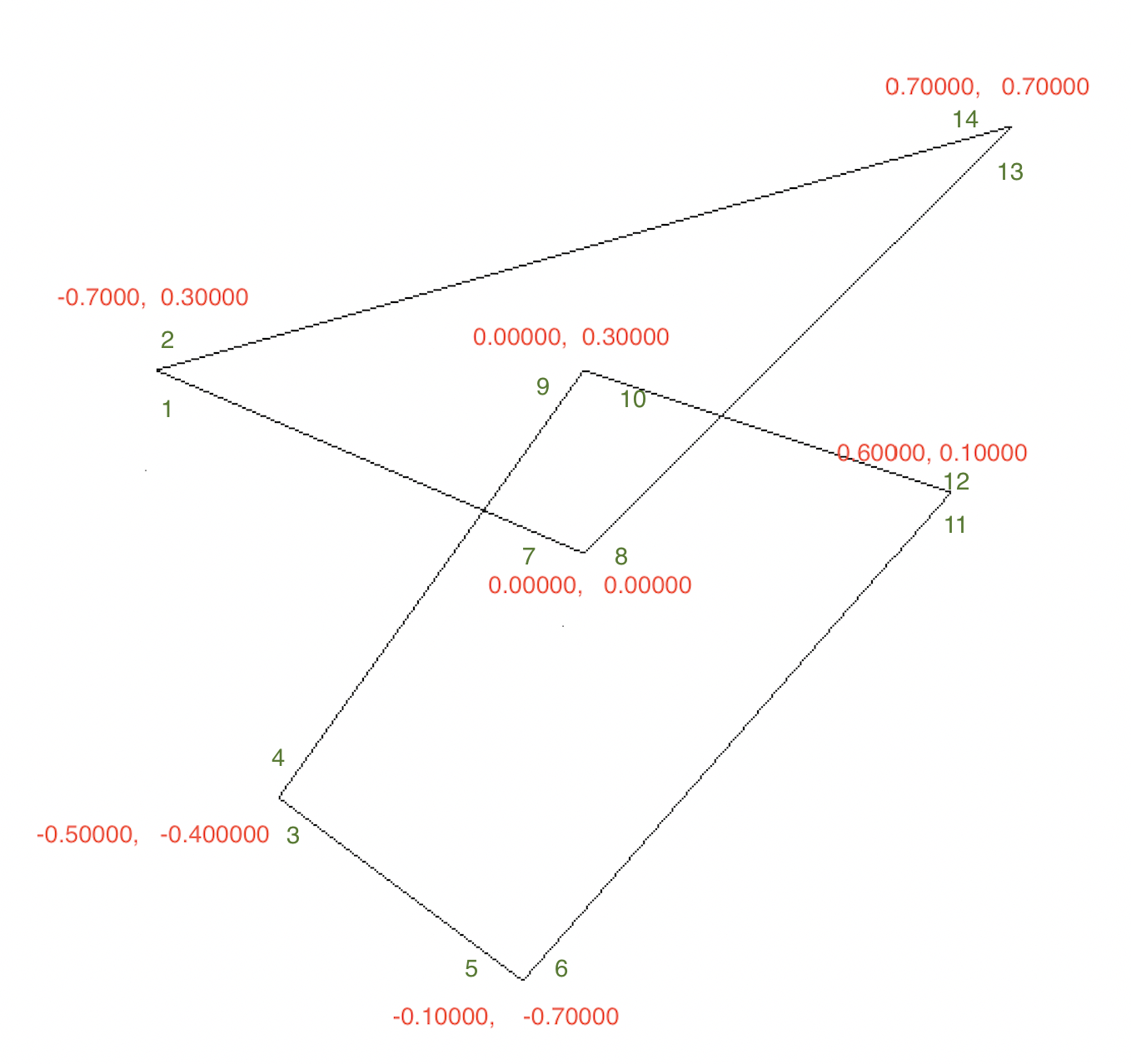
　　当我们输入两组多边形时，需要考虑相交的情况，作者根据已有顶点排序创造性的用扫掠算法处理边相交的情况。所谓扫掠算法读者可以参考底部的链接，这里作者假想有一条垂线从左至右的移动，每次移动跳到下一个线段的端点或线段交点处，每次只对比在垂线上相邻线段是否相交。如图所示：

 

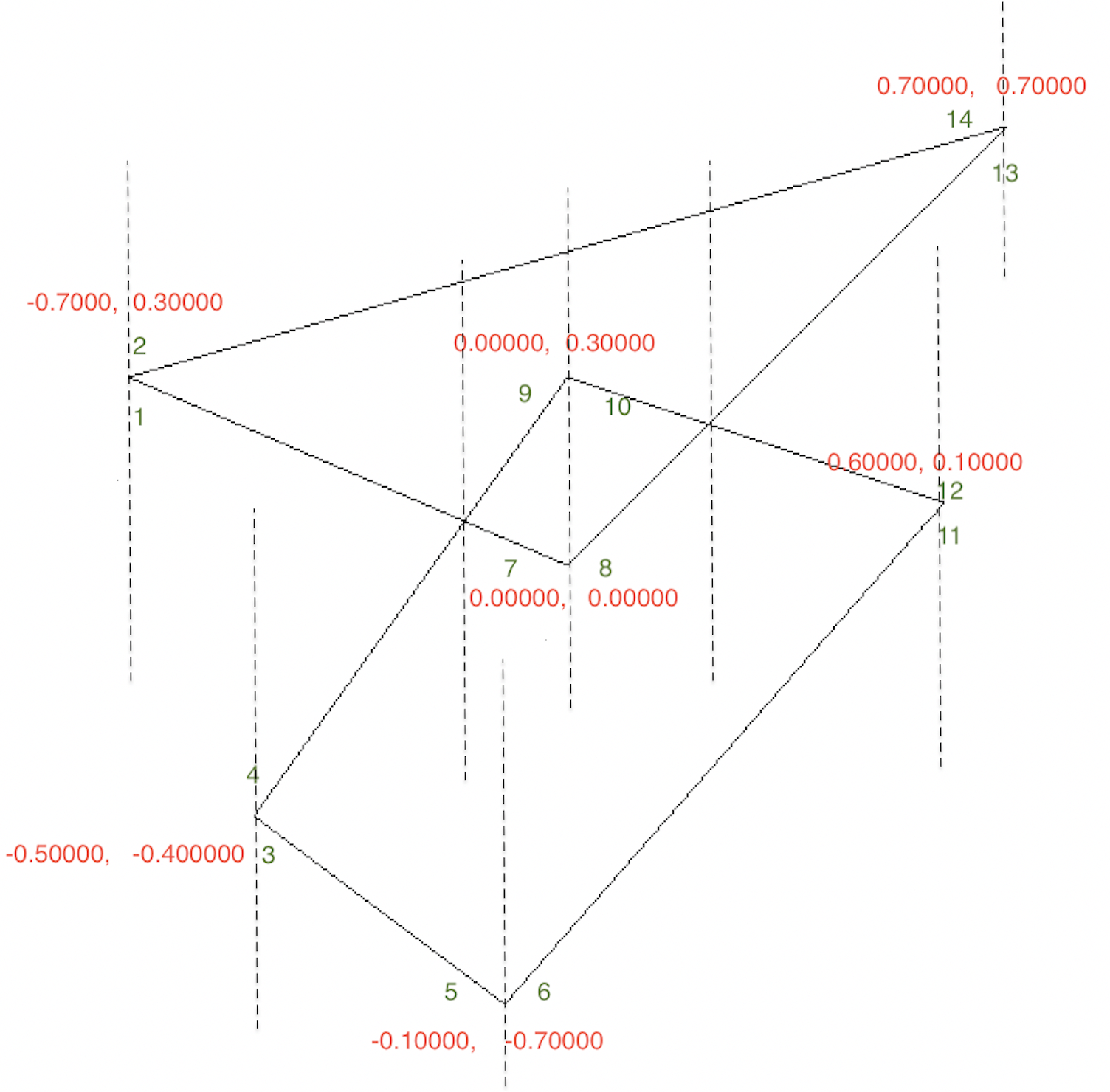
　　1. 垂线首先会跳到 1 位置，这时垂线上只有一条边；

　　2. 接着跳到 2 位置，这时候垂线上有 12 两条边，它会计算 12 是否相交，判断 12 相交于端点所以直接忽略；

　　3. 再次会跳到 3 位置，这是垂线上有 123 这三条边，它会计算新加入的 3 边与它相邻的边是否相交，与 3 相邻的边只有 1；

　　4. 接着会跳到 4 位置，4 边加入队列，与 4 相邻的边有 1 和 3，34 相交于端点直接忽略，接着发现 4 和 1 相交，计算出新的端点 p，端点 p 将 1 和 4 分成四条线段，这个 p 点分别成为 1 的右端点，4 的右端点，7 的左端点和 9 的左端点；

　　5. 接着会跳到 4 的右端点 p，将（4 -> p）这条线从队列上删除，这时会对比删除线的前面和后面也就是（3 -> 5）和（1 -> p）是否相交；

　　6. 接着会跳的 1 的右端点 p，将（1 -> p）这条线从队列上删除，也会对比删除线的前面和后面也就是（3 -> 5）和（2 -> 14）是否相交；

　　7. 接着会跳到 7 的左端点 p，这时会对比这条线分别于前后两条线是否相交，也就是（3 -> 5）和（2 -> 14）；

　　8. 同理跳到 9 的左端点 p，分别对比（p -> 7）和（2 -> 14）于这条线是否相交；

　　9. 之后同理遇到左端点，就分别判断新加入的线跟它的前、后是否相交；遇到右端点，将右端点在所在的线从队列中删除，同时还要对比删除的线的前后是否相交，原因是该线删除后，它的前后就成为相邻线段了。

 

　　因为垂线是假想的，到底实际是怎么操作的呢？我们看线的移动顺序就是我们每次从小顶堆中拿到的数据的顺序，我们还需要的就是对边从上到下排序，这样才能拿到相邻的线段。这里作者使用了 set 容器，set 容器有个排序函数，它保证每次从小顶堆中拿到的数据再按从下到上依次插入到容器中。

　　到目前，我们一直忽略属性是怎么计算的，现在该讨论它了。由于我们经过小顶堆排序和 set 容器排序后，它就保证了每一步，set 容器中第一个数据一定是最左边、最下面的那条边，所以这条边肯定是外轮廓，它的属性被直接赋予 inOut:false, otherInOut:true。其次作者定义：1.如果新插入的边和它的前面那条边属于同一类多边形，那么新插入的边的 inOut 属性根据之前边的 inOut 属性值取反，并传递它的 otherInOut 属性。2.如果不属于同一类多边形，那么这条边的 inOut 属性根据前面边的 otherInOut 属性值取反，它的 otherInOut 属性值与之前边的 inOut 属性值保持一致。 笔者对第二点做下抛砖引玉，因为根据排序规则，如果新插入的边和之前的边不属于同一类多边形的话，之前的边要不是顶边，要不是底边，如果遇到外轮廓底边，inOut 属性一定是 false，所以新插入的边它不可能是外轮廓了，它的外部已经有另一类多边形的底边了，它的 otherInOut 也是 false，如果遇到洞的底边，洞底边的 inOut 为 true，新插入的边也一定是一个外轮廓，它的 otherInOut 也是 true；如果遇到外轮廓顶边，顶边的 inOut 一定 true，那么新插入的边一定是外轮廓，它的 otherInOut 也为 true，如果遇到洞的顶边，顶边的 inOut 一定是 false，说明新插入的边被包含多边形的内部，它不可能是个外轮廓，otherInOut 也是 false。同样道理，新插入的边 inOut 属性的确定，字数较多，读者自行思考 😅

 

　　我们之前一直在讨论理论，现在笔者结合具体场景，还是利用上图（这个图比较简单、有代表性），来详细的介绍边裁剪和属性计算的流程：

　　1. 从小顶堆中得到 1 顶点对应的 sweepevent，将其插入到 set 容器中，由于它目前在容器中是第一个，最左侧的边肯定是外轮廓，所以 inOut:false，otherInOut:true;

　　2. 从小顶堆中得到 2 顶点对应的 sweepevent，将其插入到 set 容器中，目前 set 中的排序是：1 -> 2，因为属于同一个类多边形且位置相同的顶点，2 的属性根据 1 属性计算得到，inOut:true，otherInOut:true，这时判断该 sweepevent 和之前 1 是否相交;

　　3. 从小顶堆中得到 3 顶点对应的 sweepevent，将其插入到 set 容器中，目前 set 中的排序是：3 -> 1 -> 2，3 边目前是最左边最底下的边，所以 inOut:false，otherInOut:true，这时判断 3、1 是否相交，由于相交于端点，故忽略；

　　4. 从小顶堆中得到 4 顶点对应的 sweepevent，将其插入到 set 容器中，目前 set 中的排序是：3 -> 4 -> 1 -> 2，4 和 3 属于同一类多边形且位置相同，4 的属性根据 3 计算得到，inOut:true，otherInOut:true，这时判断 4 与 3、1 是否相交。由于与 3 相交与端点，直接忽略，与 1 相交于 p 点，这时p点将[1,7]和[4,9]两线段分割成[1,p],[4,p],[p,7]和[p,9]四条线段，所以根据 sweepevent 中的 otherEvent 指针关系，4 和 1 的右端点原本分别指向 9 和 7，9 和 7 的左端点原本分别指向 4 和 1，现在将 4 和 1 的右端点重新指向相同位置的 p 端点(即  4对应的sweepevent{left: true, otherEvent指向 其otherEvent指向左端点4的sweepevent对象}，1对应的sweepevent{left: true, otherEvent指向 其otherEvent指向左端点1的sweepevent对象})，将 9 和 7 的左端点也分别指向相同位置的 p 端点(即  9对应的sweepevent{left: false, otherEvent指向 其otherEvent指向右端点9的sweepevent对象}，7对应的sweepevent{left: false, otherEvent指向 其otherEvent指向右端点7的sweepevent对象})，并将四个 p 端点(sweepevent{left: false, otherEvent指向1}、sweepevent{left: false, otherEvent指向4}、sweepevent{left: true, otherEvent指向7}、sweepevent{left: true, otherEvent指向9})依次插入小顶堆中；

　　5. 从小顶堆中得到 4 的右端点对应的 sweepevent，由于这个端点是右端点，所以从 set 中删除 4 这个 sweepevent，目前 set 中的排序是：3 -> 1 -> 2，这时 3 和 1 又成为相邻关系，判断它两是否相交；

　　6. 从小顶堆中得到 1 的右端点对应的 sweepevent，由于这也是右端点，所以从 set 中删除 1 这个 sweepevent，目前 set 中的排序是：3 -> 2，这时 3 和 1 成为相邻关系，判断它两是否相交；

　　7. 从小顶堆中得到 7 的左端点对应的 sweepevent，将其插入到 set 容器中，目前 set 中的排序是：3 -> 7 的左 -> 2，7 的左边属性根据 3 计算得到，这两个不属于同一类，因此 7 的左边属性为：inOut:false，otherInOut:false，这时判断 7 的左分别与 3 和 2 是否相交；

　　8. 从小顶堆中得到 9 的左端点对应的 sweepevent，将其插入到 set 容器中，目前 set 中的排序是：3 -> 7 的左 -> 9 的左 -> 2，9 的左根据 7 的左属性计算得到，这两个不属于同一类，因此 9 的左边属性为：inOut:true, otherInOut:false，这时判断 9 的左和 7 的左、2 是否相交；

　　9. 从小顶堆中得到 5 顶点对应的 sweepevent，由于它是右端点，将其左端点 3 从 set 容器中删除，之后的相交事件 3 -> 5 这条边没有用了;

　　10. 从小顶堆中得到 6 顶点对应的 sweepevent，由于它是左端点，将其插入 set 容器中，目前 set 中的排序是：6 -> 7 的左 -> 9 的左 -> 2，6 目前是最底下的边，它肯定是外轮廓，边属性为：inOut:false，otherInOut:true;

　　......

　　最终计算结果如下图所示：

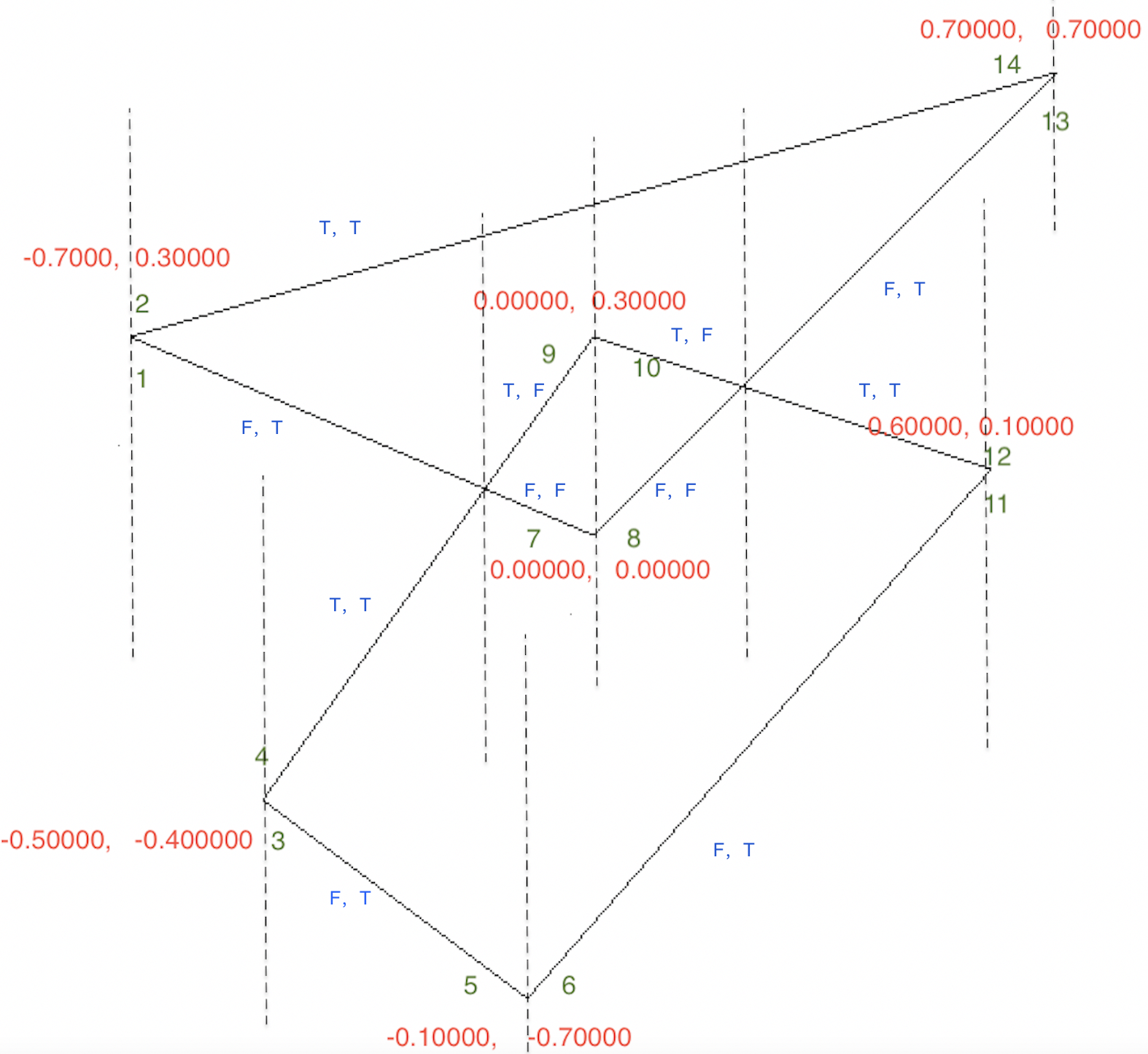
边重组

　　根据前面拓扑关系小节中讨论的情况，在两组多边形相交的情况下，根据不同的结果，有不同的边选择方法大体如下：

　　1.A ⋃ B：选择 otherInOut 为 true 的边；

　　2.A ⋂ B：选择 otherInOut 为 false 的边；

　　3.A - B：如果边属于被裁剪对象，选择 otherInOut 为 true 的边；如果边属于裁剪对象，选择 otherInOutw 为 false 的边；

　　4.A ⋃ B - A ⋂ B：选择所有边。

　　以上讨论是普通情况，还记得我们在边求交小节中讨论边重叠情况么，在这需要重新讨论下对此情况该怎么选择边，不然会造成选择后的边出现重叠。边与边重叠的情况如下图所示，我们只讨论 c 图，因为其他图的线段在经过裁剪后都将归结于图 c 的情况。对于图 c，如果出现两条边完全重叠，在边选择时候我们自然需要舍弃其中一条边，但是重点在于剩下的那条边并不总是需要。

　　

　　请看下图，重叠的边在不同的情况下被选择性过滤，在第一行中，重叠的边只被选择作为 A ⋃ B 和 A ⋂ B 的边界，而在第二行中作为 A-B 边界。在第一行中，两条重叠的边有相同的 inOut 属性，都为 false，而在第二行中，两条边的 inOut 属性不同。因此作者定义：

　　1.如果两重叠的边有相同的 inOut 属性，且当布尔运算是 A ⋃ B 和 A ⋂ B 时，则选择该边；

　　2.如果两重叠的边有不同的 inOut 属性，且当布尔运算是 A-B 时，则选择该边。

　　

　　最后我们介绍 SweepEvent 类中其他几个属性以及 Contour、Polygon 类，SweepEvent 的这几个属性用于将顶点按拓扑关系依次连接起来，最终将得到所需要的数据 polygon。

struct SweepEvent {
    bool inResult; // 是否是选择的边
    SweepEvent *prevInResult; // 离它最近、在其下面且也是被选择的边，用于确定轮廓之间的包含关系
    unsigned int pos; // 用于指引同一线段另一个端点对应的sweepevent在数据集中的位置
    unsigned int contourId; // 轮廓id
    bool external; //是否是外轮廓
    ...
}
class Contour {
    vector<Point2D> points; // 轮廓的顶点数据
    vector<unsigned int> holes; // 该轮廓的洞，在Polygon中的位置
    void addHole(unsigned int); // 指定洞在Polygon中的位置
    void setClockwise(); // 设置顶点排序
    ...
}
class Polygon {
    vector<Contour> contours; // 多边形的所有轮廓数据
    ...
}

　　

　　在进行边裁剪、属性计算时，程序根据每条边 otherInOut 和 inOut 属性以及所设定的布尔操作，会确定该边是否是选择边，并赋给 inResult，同时也会计算它的 prevInResult。在最后一步将顶点按序连接时，就将 inResult 为 true 的 sweepevent 依次放进数组中，并保证从左到右，相同位置顶点连续，然后从下到上的排序规则。

在遍历这个数组时，会将每个 sweepevent 对象的 pos 属性值设定为同一线段另一个端点在数组中的位置，如下图所示。

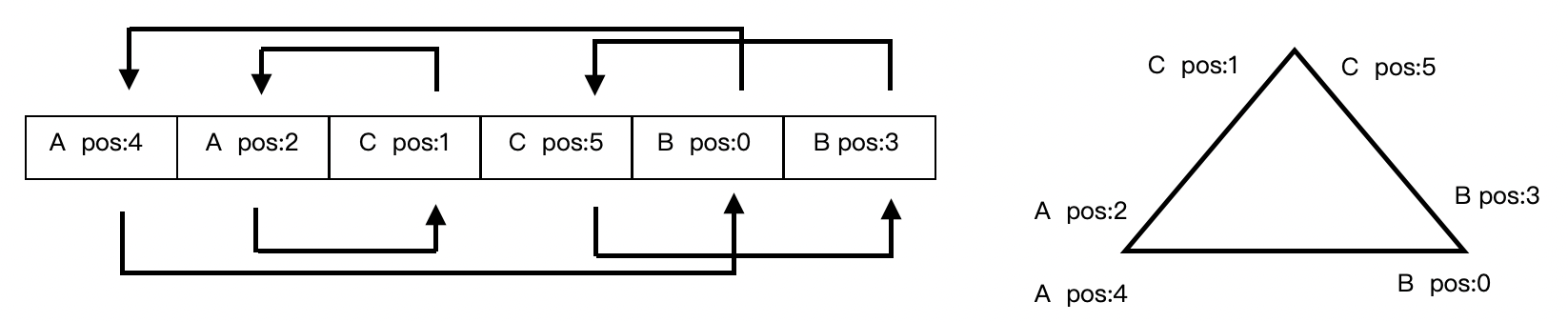
　　这样做的目的是：布尔运算结果会有洞产生，因此多个轮廓的 sweepevent 在数组中按空间位置交错排列，因为左边端点总是最先遍历:

　　1.当遍历到Apos:4这个sweepevent -->

　　2.根据pos位置获得另一个端点Bpos:0 -->

　　3.对 B 的位置再进一位，得到 B pos:3 -->

　　4.根据 pos:3 得到这条边的另一个端点 C pos:5 -->

　　5.对 C 的位置减一位的 C pos:1 -->

　　6.根据 pos:1 得到 A pos:2 -->

　　7.A 与起始点位置相同，这样单个轮廓(Contour 对象)提取完成。

　　还有轮廓与轮廓的包含关系是通过每条边的 prevInresult 属性来判断的，最外层轮廓总是先被提取，因此它就是外轮廓，它的每条边 external 就是 true，当遍历到内部轮廓时，通过判断 preInResult 的那条边是否是外轮廓，或者那条边有父轮廓（这两个洞同被外轮廓包含），那么就可以指定外轮廓与子轮廓的包含关系(addHole)。同时设定最外层轮廓他的 level 为 0，父轮廓的子轮廓 level 为 1，子轮廓的子轮廓 level 为 2，依次类推，将 level 为奇数的轮廓顶点数据按逆时针排序，偶数为顺时针排序。

讨论

　　笔者曾在前言中阐述了使用此算法的条件，其中说明了算法不关心顶点输入的顺序，那是因为算法有自己处理顶点的顺序，就是之前我们讨论的小顶堆排序和 set 排序，不管是顺时针还是逆时针，算法都将其变成自己处理的顺序；其次同一多边不能有边重叠，根据我们在边重组讨论的情况，边重叠会造成不同的计算结果，对于同一多边形，边重叠影响边属性的计算，从而造成计算结果并不是我们所需要的。

致谢

　　感陈大师向我提出这个需求，感谢李师妹给我提供论文材料，感谢付同学在博客搭建方面给我提供的建议。

　　路曼曼其修远兮，吾将上下而求索。

引用文献

[1]F Martínez, Ogayar C , JR Jiménez, et al. A simple algorithm for Boolean operations on polygons[J]. Advances in Engineering Software, 2013, 64(oct.):11-19.

作者源码

http://www4.ujaen.es/~fmartin/bool_op.html

网页资料

1.N 条线段求交的扫描线算法：https://www.freesion.com/article/8915463859/

2.算法可视化：https://unpkg.com/polybooljs@1.2.0/dist/demo.html