树状数组
简介
树状数组是一种支持在 \(\log n\) 的时间内完成 单点修改 和 区间查询 的数据结构,并且它的 代码量极小。
事实上,树状数组能解决的问题是线段树能解决的问题的子集:树状数组能做的,线段树一定能做;线段树能做的,树状数组不一定可以。然而,树状数组的 代码要远比线段树短,时间效率常数也更小,因此很有学习价值。
有时,在差分数组和辅助数组的帮助下,树状数组还可解决更强的 区间加单点值 和 区间加区间和 问题。
首先你得知道,普通的树状数组维护的信息一定要满足 结合律 并且 可差分 ,如加法、乘法、异或等。
为什么是这样呢?因为事实上,树状数组维护的是一个类似前缀和的东西,所以维护的信息自然就要满足 结合律 并且 可差分。
查询
先考虑查询一个前缀区间 \([1,x]\)。
首先有一个显然的结论,任意一个数都可以表示成若干个 2的整数次幂 相加的形式。
由此,查询时我们考虑把 \([1,x]\) 拆成若干个 长度为2的整数次幂的区间 合并的形式。
现在问题是,怎么划分这些 长度为2的整数次幂的区间 ?
我们先考虑怎么找到这些区间的长度,这显然就简单了,转换为 二进制 就一目了然了。
举个例子,\(n=10\) 时,转换成二进制就是 1010 ,很快能找到两个长度 \(10_2\) 和 \(1000_2\) (\(x_2\) 这表示在二进制下的 \(x\))。
所以我们只要在 \([1,n]\) 内酌情划分2个长度为 \(10_2\) 和 \(1000_2\) 的区间就好了。
树状数组是这样划分的,它会把二进制的 从右往左看 ,每看到一个 1 就按照往左划分一个长度为这个 1 对应的位权的区间。
如,当 \(n=11\) 时,它是这样划分成了这三个区间 \([11,11],[9,10],[1,9]\) 。
那么怎样找到这些被划分的区间呢?
设 \(tr_x\) 管辖区间 \([x-lowbit(x)+1,x]\) ,其中 \(lowbit(x)\) 表示 \(x\) 在 二进制下从右往左看第一个 1 的位权 。
怎么计算 \(lowbit(x)\) 呢?由位运算知识可得 lowbit(x)=x&-x。
原理如下,摘自 oiwiki:
将
x的二进制所有位全部取反,再加 1,就可以得到-x的二进制编码。例如,6的二进制编码是110,全部取反后得到001,加1得到010。设原先
x的二进制编码是(...)10...00,全部取反后得到[...]01...11,加1后得到[...]10...00,也就是-x的二进制编码了。这里x二进制表示中第一个1是x最低位的1。
(...)和[...]中省略号的每一位分别相反,所以x & -x = (...)10...00 & [...]10...00 = 10...00,得到的结果就是lowbit。
看完以上内容,你应该知道怎么查询了,从最右边的区间往左跳一下合并不就好了嘛。
其中 \([x-lowbit(x)+1,x]\) 的左边一个区间不就在 \(tr_{x-lowbit(x)}\) 里嘛。
至于边界就是 \(x=0\) 。
int getsum(int x){ //前缀区间和[1,x]
int res = 0;
for(; x > 0; x -= lowbit(x)) res += tr[x];
return res;
}
现在考虑查询一个区间 \([l,r]\) ,因为维护的是 前缀区间并且满足结合律,所以结果就是 getsum(r)-getsum(l-1) 。
修改
考虑将 \(a\) 数组的第 \(x\) 个数加上某个数。
我们的目标是快速正确地维护 \(tr\) 数组。为保证效率,我们只需修改 管辖了 \(a[x]\) 的所有的 \(tr[y]\) ,因为其他的 \(tr[y]\) 显然 没有发生变化。
首先我们知道,\(tr[x]\) 肯定包含 \(a[x]\) ,而且 \(tr[k](k<x)\) 肯定不包含 \(a[x]\) 。
所以可以确定如果 \(tr[k]\) 要包含 \(a[x]\) ,那么 \(x\le k\) 。
既然都已经知道 \(tr[x]\) 包含 \(a[x]\) 了,那么对于 \(tr[k](k>x)\) , 你都在 \(x\) 的右边了 ,你管辖区间的长度至少得大于 \(lowbit(x)\) 吧(不理解自己画图)。
显然,往右看,第一个这样的 \(k=x+lowbit(x)\) 。
仔细思考,这相当于一个 二进制进位的过程。
你现在应该知道怎么修改了,\(x\) 往左跳再修改一下不就好了嘛。 其中边界显然就是 \(x>n\) 。
void update(int x, int k){ //将第x个元素加上k。
for(; x <= n; x += lowbit(x)) tr[x] += k;
}
建树
当然你可以用 update \(n\log n\) 建树,这里介绍两种 \(O(n)\) 建树法。
以维护前缀和为例
方法一:直接按照 \(tr\) 的定义用前缀和优化。
方法二(类似单点修改):
因为 tr[i+lowbit(i)] 一定包含 tr[i] (原理自行思考qwq)。
for (int i = 1; i <= n; ++i) {
tr[i] += a[i];
int j = i + lowbit(i);
if (j <= n) tr[j] += tr[i];
}
树?
Q:所以,这和树有甚么关系???
A:好像没有什么关系。
硬要扯,就是这样 (借用oiwiki的图):
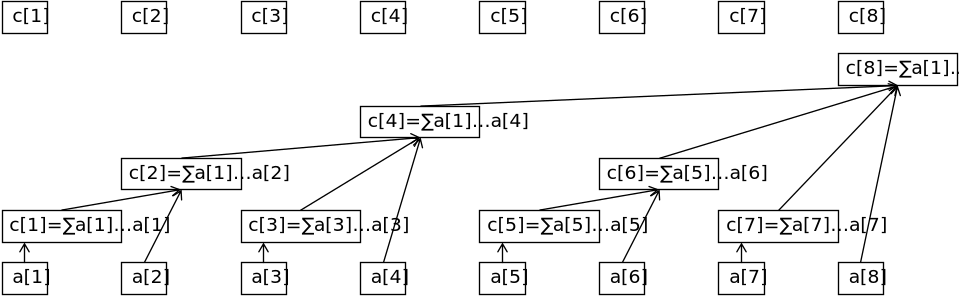


 浙公网安备 33010602011771号
浙公网安备 33010602011771号