算法学习笔记（差分约束）

差分约束算法

这个算法挺巧妙的，最初始的形态是用来处理一组不等式可能解的问题，如下题：

https://www.luogu.com.cn/problem/P5960

我们分析一下，对于不等式xi - xj <= C，移项后可得xi <= xj + C

熟悉图论的同学可以发现，这好像是最短路的松弛条件啊 d[v] <= d[u] + W

如果能够这么想那你好厉害！别在这浪费时间了所以我们就可以转化为单源最短路问题去解决啦。

我们把xi和xj当成两个结点，从xj向xi连一条权值为C的边，最后再建立一个结点0，向所有的结点连一条权值为0的边，我现在的理解是要跑单源最短路的话，那你必须确定一个顶点啊不然怎么跑。那怎么去判断解的存在性呢，显然如果顶点到任何一点的最短路存在的话，那么d[i]就是一组解；那最短路不存在不就无解了吗！什么情况下最短路不存在呢？目前我所知道的就是当图中存在负环的时候，最短路就不存在（因为可以无限跑这个负环使得路程无穷小）。那就spfa判环咯（先不管spfa的死活啦）

这里我还想要补充一点点细节的证明（也不知道有没有必要）就是我们可能会想到，如果存在这样一种情况：

 

 

 

 

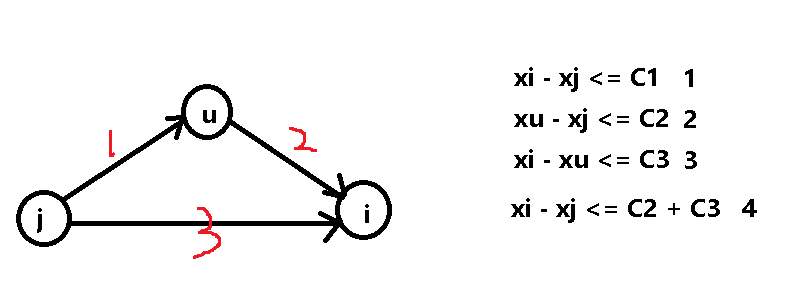
那最短路要不就跑12要不就跑3，那可能对应会有一个不等式（1）或者两个不等式（2、3）被忽略不计吗？

事实证明不是的，我们可以把不等式2和3相加得到4，然后呢如果最短路跑3的话，那么说明C1 < C2 + C3，并且不等式1成立，显然这个时候不等式4也是成立的，也就是说不等式2和3也是成立的；如果最短路跑12的话也是同理的。

 

代码实现也是非常之简单的！

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>

using namespace std;
const int N = 5e3 + 10,INF = 0x3f3f3f3f;
int n,m;int d[N];
struct edge{
    int next,to,w;
}e[N << 2];
int head[N],cnt;
void add(int u,int v,int w){
    e[++ cnt].next = head[u];
    e[cnt].to = v;
    e[cnt].w = w;
    head[u] = cnt;
}
bool vis[N];
int inq[N];
bool spfa(int s){
    queue<int> q;
    for(int i = 1;i <= n;i ++) d[i] = INF;
    d[s] = 0;
    q.push(s);vis[s] = 1;
    while(!q.empty()){
        int u = q.front();q.pop();
        vis[u] = 0;
        for(int i = head[u];i;i = e[i].next){
            int v = e[i].to;
            if(d[v] > d[u] + e[i].w){
                d[v] = d[u] + e[i].w;
                if(!vis[v]){
                    vis[v] = 1;
                    q.push(v);
                    inq[v] ++;
                    if(inq[v] > n) return true;
                }
            }
        }
    }
    return false;
}

int main(){
    scanf("%d%d",&n,&m);
    for(int i = 0;i < m;i ++){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        add(b,a,c);
    }
    for(int i = 1;i <= n;i ++) add(0,i,0);
    if(spfa(0)) puts("NO");
    else{
        for(int i = 1;i <= n;i ++) printf("%d ",d[i]);
    }
    return 0;
}

但是问题并不像你想象中那么简单!

题目一般都不会直接就扔给你一堆不等式，通常都需要你自己去寻找题意中的不等式关系；而且可能还会是另一种变体

用最长路处理最小值问题

比如说这道题：https://www.luogu.com.cn/problem/P3275

题目有两个严格小于或大于的条件，这种容易转换，比如说A < B，那么在这道题中（可能不同题目要求不同）就可以转换为，A + 1 <= B

为啥要跑最长路？因为题目要求嘞，比如这道题它是说要满足所有小朋友的要求，如果跑最短路的话就可能会漏掉某些边（其实我也还不是很懂）

但是还是AC了.....

AC代码：

 

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>

using namespace std;
const int N = 1e5 + 10;
typedef long long ll;
struct edge{
    int next,to,w;
}e[N << 2];
int head[N],cnt;
void add(int u,int v,int w){
    e[++ cnt].to = v;
    e[cnt].next = head[u];
    e[cnt].w = w;
    head[u] = cnt;
}
int n,m;

ll d[N];bool vis[N];
int inq[N];
bool spfa(int s){
    queue<int> q;
    q.push(s);vis[s] = 1;
    while(!q.empty()){
        int u = q.front();q.pop();
        vis[u] = 0;
        for(int i = head[u];i;i = e[i].next){
            int v = e[i].to;
            if(d[v] < d[u] + e[i].w){
                d[v] = d[u] + e[i].w;
                if(!vis[v]){
                    vis[v] = 1;
                    q.push(v);
                    inq[v]++;
                    if(inq[v] > n) return true;
                }
            }
        }
    }
    return false;
}
int main(){
    scanf("%d%d",&n,&m);
    for(int i = 1;i <= m;i ++){
        int a,b,c;
        scanf("%d%d%d",&a,&b,&c);
        if(a == 1) add(b,c,0),add(c,b,0);
        else if(a == 2){
            if(b == c){cout << - 1 << endl;return 0;}
            add(b,c,1);
        }
        else if(a == 3) add(c,b,0);
        else if(a == 4){
            if(b == c){cout << - 1 << endl;return 0;}
            add(c,b,1);
        }
        else add(b,c,0);
    }
    for(int i = n;i >= 1;i --) add(0,i,1);
    if(spfa(0)){
        cout << -1 << endl;
    }
    else {
        ll ans = 0;
        for(int i = 1;i <= n;i ++) ans += d[i];
        cout << ans << endl;
    }
    return 0;
}