Codeforces Round 857 (Div. 1)

一些fst的震撼。。。
A
看完题慌了一会,感觉很仙。但想到i和j两维可以分别占几位做,然后每维相同的格子都有两个,直接设为坐标异或起来就都是0了。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N=205;
void work(){
int n,m;
cin>>n>>m;
cout<<n*m<<endl;
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
printf("%d ",i*256+j);
}
puts("");
}
}
int main(){
int T; cin>>T; while(T--) work();
return 0;
}
B
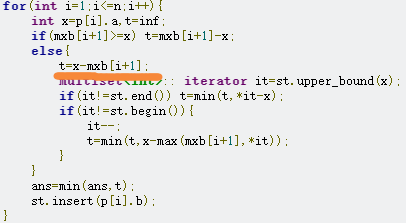
原本没加这句话,如果set里没有不大于x的元素,就没法算到后面的最大值。
当时可能默认if里面都会做到,但其实两个if只是利用前面可选的优化答案而已,初始值肯定是要设的,这也和前面的情况形成对称。
以后应该多理顺一下每句话的意义,然后多考虑特殊情况!
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+5,inf=1e9+5;
int n;
struct node{
int a,b;
}p[N];
bool cmp(node u,node v){
return u.a<v.a;
}
int T,mxb[N];
void work(int id){
cin>>n;
for(int i=1;i<=n;i++){
scanf("%d%d",&p[i].a,&p[i].b);
}
sort(p+1,p+n+1,cmp);
mxb[n+1]=-inf;
for(int i=n;i;i--) mxb[i]=max(mxb[i+1],p[i].b);
multiset<int>st;
st.clear();
int ans=inf;
for(int i=1;i<=n;i++){
int x=p[i].a,t=inf;
if(mxb[i+1]>=x) t=mxb[i+1]-x;
else{
t=x-mxb[i+1];
multiset<int>:: iterator it=st.upper_bound(x);
if(it!=st.end()) t=min(t,*it-x);
if(it!=st.begin()){
it--;
t=min(t,x-max(mxb[i+1],*it));
}
}
ans=min(ans,t);
st.insert(p[i].b);
}
cout<<ans<<endl;
}
int main(){
cin>>T; for(int i=1;i<=T;i++) work(i);
return 0;
}
C
node里面放vector,并且cmp里参数没加&,会TLE!因为根据实验证明,sort不保证每个数的排序次数是均摊的,可能出现一些数排O(n)次的情况。
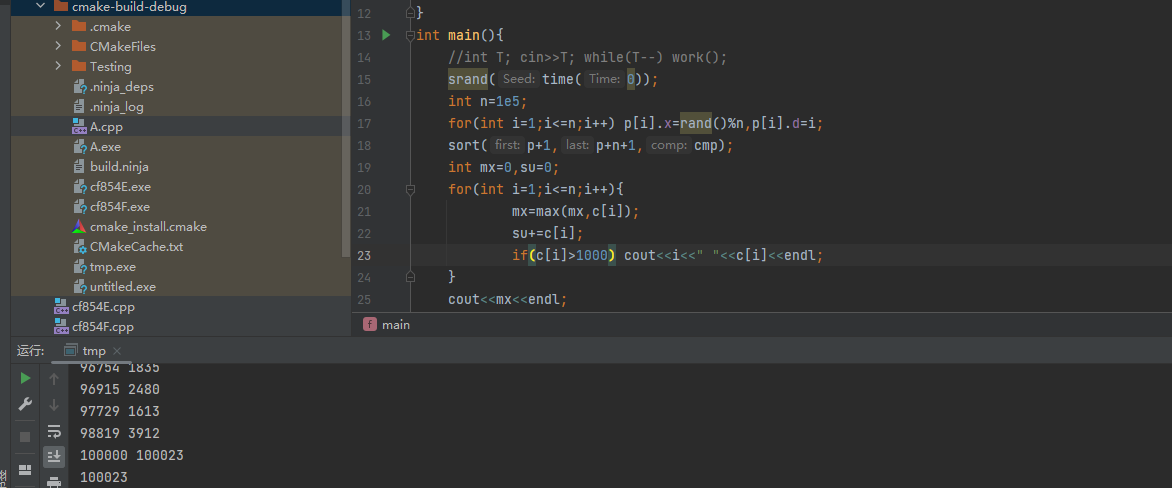
没加&的时候,排序时会把整个结构体复制出来排序,就寄了。加了&之后就只会比较一个数。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N=5e5+5,inf=1e9+5;
int n;
struct node{
vector<int>h;
int sz,lt;
}p[N];
bool cmp(node u,node v){
return u.lt<v.lt;
}
int dsc[N],mx[N],f[N],m;
void upd(int x,int y){
while(x<=m) mx[x]=max(mx[x],y),x+=x&-x;
}
int cnt(int x){
int mxa=0;
while (x) mxa=max(mxa,mx[x]),x-=x&-x;
return mxa;
}
int T;
void work(){
cin>>n;
m=0;
for(int k,x,i=1;i<=n;i++){
scanf("%d",&k);
p[i].lt=p[i].sz=0;
p[i].h.clear();
while(k--){
scanf("%d",&x);
dsc[++m]=x;
if(!p[i].lt || x>p[i].lt){
p[i].lt=x;
p[i].h.push_back(x);
p[i].sz++;
}
}
}
sort(dsc+1,dsc+m+1);
m=unique(dsc+1,dsc+m+1)-dsc;
for(int i=1;i<=n;i++){
for(int j=0;j<p[i].sz;j++) p[i].h[j]=lower_bound(dsc+1,dsc+m+1,p[i].h[j])-dsc;
p[i].lt=p[i].h[p[i].sz-1];
}
sort(p+1,p+n+1,cmp);
for(int i=1;i<=m;i++) mx[i]=0;
int ans=0;
for(int i=1;i<=n;i++){
f[i]=0;
for(int j=0;j<p[i].sz;j++){
f[i]=max( f[i],cnt(p[i].h[j]-1)+p[i].sz-j);
}
upd(p[i].lt,f[i]);
ans=max(ans,f[i]);
}
cout<<ans<<endl;
}
int main(){
int T; cin>>T; while(T--) work();
return 0;
}
D
注意到对于走过的一段城市,停下表演的城市肯定是像C题那样,是前缀最大值的城市;并且,每次都是在该城市买到恰好够到达下一个前缀最大值的城市。那么把每对点间的距离预处理一下,再按照{天数,剩下的钱}为优先级跑最短路即可。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=805,M=1e4+5;
const ll inf=1e15;
int n,m,p,w[N];
int hd[N],to[M],nx[M],wl[M],tt;
void add(int u,int v,int l){
nx[++tt]=hd[u];
to[hd[u]=tt]=v;
wl[tt]=l;
// cout<<"add:"<<u<<" "<<v<<" "<<hd[u]<<endl;
}
ll dis[N][N];
struct node{
int u;
ll t,r;
bool operator <(const node& v) const{
return t>v.t || (t==v.t && r<v.r);
}
};
void find(int s){
priority_queue<node>q;
for(int i=1;i<=n;i++) dis[s][i]=inf;
dis[s][s]=0;
q.push((node){s,0,0});
while(!q.empty()){
node u=q.top();
q.pop();
//cout<<"u="<<u.u<<" "<<hd[u.u]<<endl;
for(int e=hd[u.u];e;e=nx[e]){
int v=to[e];
//cout<<"vv="<<v<<endl;
if(u.t+wl[e]<dis[s][v]){
//cout<<"v="<<v<<endl;
dis[s][v]=u.t+wl[e];
q.push((node){v,dis[s][v],0});
}
}
}
//cout<<"s="<<s<<endl;
//for(int i=1;i<=n;i++) cout<<dis[s][i]<<" "; puts("");
}
ll ds[N],rs[N];
void work(){
cin>>n>>m>>p;
for(int i=1;i<=n;i++) scanf("%d",&w[i]);
tt=0; memset(hd,0,sizeof(hd));
while(m--){
int u,v,l;
scanf("%d%d%d",&u,&v,&l);
add(u,v,l);
}
for(int i=1;i<=n;i++) find(i);
priority_queue<node>q;
for(int i=1;i<=n;i++) ds[i]=inf,rs[i]=0;
ds[1]=0; rs[1]=p;
q.push((node){1,0,p});
while(!q.empty()){
node u=q.top();
q.pop();
for(int v=1;v<=n;v++) if(v!=u.u && dis[u.u][v]<inf){
ll k;
if(u.r>=dis[u.u][v]) k=0;
else k=(dis[u.u][v]-u.r-1)/w[u.u]+1;
node vv=(node){v,u.t+k,(u.r+k*w[u.u])-dis[u.u][v]};
if(vv.t<ds[v] || (vv.t==ds[v] && vv.r>rs[v])){
ds[v]=vv.t;
rs[v]=vv.r;
q.push(vv);
}
}
}
if(ds[n]<inf) printf("%lld\n",ds[n]);
else puts("-1");
}
int main(){
int T; cin>>T; while(T--) work();
return 0;
}
E
之后看了下,想了个树剖+分治+哈希+树状数组+启发式合并的做法,感觉很对,并对cf会出这种板套板的题目表示震撼,然而调了半天还没调出来。。。先占个坑
upd:补完了,一些6k的震撼。。。

思路其实挺简单的,就五个板子套在一起:
1.先树剖把路径转化成log段区间,就变成序列上的问题。
2.发现是个合并集合的过程,则有效的合并次数是\(O(n)\)的。考虑如何在序列上的两段等长序列中,用\(O(对应位置所属集合不同的对数\times log)\)找出,对区间分治即可。
3.上述做法需要判断并查集中fa数组的两段区间是否相等,故用哈希。
4.并查集需要修改并且实时维护每个点所属集合,故用启发式合并。
5.单点修改区间查询,故用树状数组。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
typedef unsigned long long ll;
const ll B=793999;
const int N=4e5+5,P=1e9+7;
inline int M(int x,int y){
return 1ll*x*y%P;
}
inline int fpw(int a,int x){
int s=1;
for(;x;x>>=1,a=1ll*a*a%P) if(x&1) s=1ll*s*a%P;
return s;
}
ll pw[N];
int n,dn[N],fa[N],mx[N],mn[N],sz[N],ans=1;
vector<int>sn[N];
struct interval{
int l,r;
int lenth(){
return abs(r-l)+1;
}
void print(){
cout<<"interval:"<<l<<" "<<r<<endl;
}
/*bool operator < (const interval& u) const {
return l<u.l;
}*/
};
struct BIT{
ll A[N];
inline void init(){
for(int i=1;i<=n;i++) A[i]=0;
}
inline void upd(int x,ll y){
//printf("upd: x=%d y=%d\n",x,y);
while(x<=n) A[x]+=y,x+=x&-x;//cout<<x<<endl;
}
inline ll cnt(int x){
ll s=0;
while(x) s+=A[x],x-=x&-x;//cout<<x<<endl;
return s;
}
}bit[2];
void init(){
pw[0]=1;
//cout<<"n="<<n<<endl;
for(int i=1;i<=n;i++) scanf("%d%d",&mx[dn[i]],&mn[dn[i]]);
for(int i=1;i<=n;i++){
pw[i]=pw[i-1]*B;
fa[i]=i;
sz[i]=1;
ans=M(ans,mn[i]-mx[i]+1);
//cout<<mx[i]<<" "<<mn[i]<<endl;
//cout<<i<<" "<<ans<<endl;
sn[i].push_back(i);
}
for(int i=1;i<=n;i++) {
bit[0].upd(i, pw[i] * i);
bit[1].upd(i, pw[n - i + 1] * i);
}
}
void mdf(int u,int x){
// cout<<"mdf: u="<<u<<" fa="<<fa[u]<<" x="<<x<<endl;
bit[0].upd( u,pw[u]*(x-fa[u]) );
bit[1].upd( u,pw[n-u+1]*(x-fa[u]) );
fa[u]=x;
sn[x].push_back(u);
}
void merge(int u,int v){
//cout<<"!:"<<u<<" "<<v<<endl;
u=fa[u]; v=fa[v];
if(u==v) return;
// cout<<"merge: u="<<u<<" v="<<v<<endl;
if(sz[u]<sz[v]) swap(u,v);
ans=M(ans,fpw(max(0,mn[u]-mx[u]+1),P-2));
ans=M(ans,fpw(max(0,mn[v]-mx[v]+1),P-2));
for(int i=0;i<sn[v].size();i++){
int x=sn[v][i];
mdf(x,u);
}
mx[u]=max(mx[u],mx[v]);
mn[u]=min(mn[u],mn[v]);
//cout<<mn[u]<<" "<<mx[u]<<endl;
sz[u]+=sz[v];
ans=M(ans,max(0,mn[u]-mx[u]+1));
}
ll cnt(interval u){
//cout<<"cnt:"<<bit.cnt(u.r)<<" "<<bit.cnt(u.l-1)<<endl;
if(u.l<u.r) return (bit[0].cnt(u.r)-bit[0].cnt(u.l-1))*pw[n-u.r];
else return (bit[1].cnt(u.l)-bit[1].cnt(u.r-1))*pw[u.r-1];
}
bool chk(interval u,interval v){
// puts("chk");
// u.print(); v.print();
//cout<<cnt(u)<<" "<<pw[v.l-u.l]<<" "<<cnt(v)<<endl;
//cout<<cnt(u)<<" "<<cnt(v)<<endl;
return cnt(u)==cnt(v);
}
interval get(interval& u,int k){
if(u.l<u.r){
int tmp=u.l;
u.l+=k;
return (interval){tmp,tmp+k-1};
}
else{
int tmp=u.l;
u.l-=k;
return (interval){tmp,tmp-k+1};
}
}
void work(interval u,interval v,int len){
//if(u.l>v.l) swap(u,v);
if(chk(u,v)) return;
//cout<<"len="<<len<<endl;
// printf("work:len=%d\n",len);
// u.print(); v.print();
// puts("");
if(len==1){
merge(u.r,v.r);
return;
}
int hlf=len/2;
work(get(u,hlf),get(v,hlf),hlf);
work(u,v,len-hlf);
}
struct WeightDivide{
int fa[N],dp[N],sz[N],sn[N],tp[N],ct;
int hd[N],to[N<<1],nx[N<<1],tt;
inline void add(int u,int v){
nx[++tt]=hd[u];
to[hd[u]=tt]=v;
}
void dfs1(int u){
sz[u]=1;
for(int e=hd[u];e;e=nx[e]){
int v=to[e];
dp[v]=dp[u]+1;
dfs1(v);
sz[u]+=sz[v];
if(sz[v]>sz[sn[u]]) sn[u]=v;
}
}
void dfs2(int u){
dn[u]=++ct;
if(sn[u]) tp[sn[u]]=tp[u],dfs2(sn[u]);
for(int e=hd[u];e;e=nx[e]){
int v=to[e];
if(v==sn[u]) continue;
tp[v]=v;
dfs2(v);
}
}
void init(){
fa[1]=tt=ct=0;
for(int i=0;i<=n;i++) hd[i]=sz[i]=sn[i]=tp[i]=0;
for(int i=2;i<=n;i++) scanf("%d",&fa[i]),add(fa[i],i);
dfs1(1);
dfs2(1);
}
int lca(int u,int v){
while(tp[u]!=tp[v]){
if(dp[tp[u]]<dp[tp[v]]) swap(u,v);
u=fa[tp[u]];
}
if(dn[u]>dn[v]) swap(u,v);
return u;
}
vector<interval> find(int u,int v){
// cout<<"find:"<<u<<" "<<v<<endl;
vector<interval>h; h.clear();
int w=lca(u,v);
while(tp[u]!=tp[w]){
h.push_back((interval){dn[u],dn[tp[u]]});
u=fa[tp[u]];
}
h.push_back((interval){dn[u],dn[w]});
stack<interval>q;
while(tp[v]!=tp[w]){
q.push((interval){dn[tp[v]],dn[v]});
v=fa[tp[v]];
}
if(v!=w) q.push((interval){dn[w]+1,dn[v]});
while(!q.empty()) h.push_back(q.top()),q.pop();
//for(int i=0;i<h.size();i++) h[i].print();
return h;
}
}T;
int main(){
cin>>n;
bit[0].init();
bit[1].init();
T.init();
init();
int m;
cin>>m;
// cout<<"m="<<m<<endl;
// cout<<ans<<endl;
while(m--){
int a,b,c,d;
scanf("%d%d%d%d",&a,&b,&c,&d);
//cout<<"m="<<m<<endl;
vector<interval>u=T.find(a,b),v=T.find(c,d);
for(int i=0,j=0;i<u.size() && j<v.size();){
int lu=u[i].lenth(),lv=v[j].lenth();
//cout<<"lu="<<lu<<" lv="<<lv<<endl;
//print()
if(lu<lv){
work(u[i],get(v[j],lu),lu);
i++;
}
else if(lu==lv){
//puts("!");
work(u[i],v[j],lu);
i++; j++;
}
else{
work(v[j],get(u[i],lv),lv);
j++;
}
}
printf("%d\n",ans);
}
return 0;
}
F
考虑暴力DP,f[i][j]表示前i个,乘积为j的最大价值;考虑优化后者,发现对于一段的j是等价的,我们关心的是剩下的乘积至少要多少,那就把状态改为这个;每次转移就是枚举当前维的切分数,然后取上整,而这个可以用整出分块优化,每块取左端点即可;这样状态数是\(O(n \sqrt{k} )\),转移是\(O(n k^{ \frac{3}{4} } )\)的。
点击查看代码
#include <bits/stdc++.h>
using namespace std;
const int N=1e7+5,M=10005;
struct node{
int l,x;
}p[N];
//vector<node>
int n,k,t,a[N];
int id[N],num[N];
double f[105][M];
int main(){
cin>>n>>k;
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
int m=k-1;
for(int i=1;i<=m+1;){
int x=m/i,j;
if(x) j=m/x;
else j=i;
node u=(node){i,x+1};
p[++t]=u;
id[x+1]=t;
num[t]=x+1;
//cout<<i<<" "<<j<<endl;
i=j+1;
}
for(int i=1;i<=t;i++) f[0][i]=0;
f[0][id[k]]=1;
for(int i=1;i<=n;i++){
for(int j=1;j<=t;j++){
int m=num[j]-1;
//cout<<"m="<<m<<endl;
for(int u=1;u<=m+1;){
int x=m/u,v;
if(x) v=m/x;
else v=u;
//cout<<u<<" "<<v<<endl;
f[i][id[x+1]]=max(f[i][id[x+1]],f[i-1][j]*(a[i]/u)/a[i]);
u=v+1;
}
}
}
double ans=f[n][id[1]]*k;
if(fabs(ans)<1e-9) puts("0");
else printf("%.12lf\n",ans);
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号