AtCoder Regular Contest 153

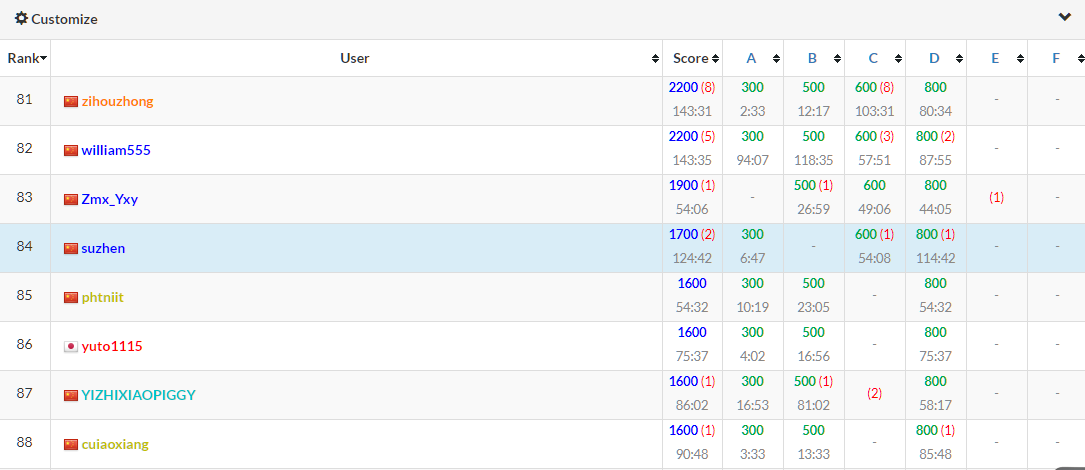
喜提全场独一无二的score！
ATC还是很友善的，如果每题等分就寄了

A

签到

B

真的是凭着实力不会做的呀。。。太菜了
发现两维可以分别做，所以考虑一维的情况，然而并不会
对于两段分别翻转，考虑先把整个序列翻转，会发现两段内部的相对位置是对的；只是需要把翻转后右边的那段平移到左边！如果把序列放到圆环上就很直观了，那么我们只需要维护一个起始点和方向，每次\(O(1)\)计算更新即可！

点击查看代码

#include<bits/stdc++.h>
using namespace std;
const int N=5e5+5;
vector<char>a[N];
struct node{
	int op,pos;
};
void shift(node& u,int x,int n){
	if(u.op==1){
		u.pos+=x;
		if(u.pos>n) u.pos-=n;
	}
	else{
		u.pos-=x;
		if(u.pos<=0) u.pos+=n;
	}
}
void rev(node& u,int n){
	u.op=!(u.op);
	shift(u,1,n);
}
int n,m;
void work(){
	cin>>n>>m;
	for(int i=1;i<=n;i++){
		a[i].resize(m+1);
		for(int j=1;j<=m;j++) scanf(" %c",&a[i][j]);
	}	
	int q; cin>>q;
	node u=(node){1,1},v=(node){1,1};
	while(q--){
		int a,b;
		scanf("%d%d",&a,&b);
		shift(u,a,n);
		rev(u,n);
		shift(v,b,m);
		rev(v,m);
	}
	//int x=u.pos,y=v.pos;
	node t=v;
	for(int i=1;i<=n;i++){
		v=t;
		for(int j=1;j<=m;j++){
			//cout<<u.pos<<" "<<v.pos<<endl;
			printf("%c",a[u.pos][v.pos]);
			shift(v,1,m);
		}
		puts("");
		shift(u,1,n);
	}
}
int main()
{
	//srand(time(0));
	//freopen("1.in","r",stdin);
	//freopen("1.out","w",stdout);
	int T=1; while(T--) work();
	return 0;
}

C

只要想到对于任意一个递增序列（我取了1-n）调整就好做了。
就根据目前的和，考虑把一个正负号差1的后缀整体加需要调整的数；注意到对于整个序列不仅可以加，还可以减，所以一开始把整个序列先向有利于后面调整的方向调整；一开始就合法的情况要特判（挂了一次）

点击查看代码

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5;
int n;
ll a[N],c,s,ans[N];
void work(){
	cin>>n;
	for(int i=1;i<=n;i++) scanf("%lld",&a[i]),s+=a[i]*i,ans[i]=i,c+=a[i];
	bool pd=0;
	//cout<<"s="<<s<<endl;

	if(s>0 && c>0){
		for(int i=1;i<=n;i++) ans[i]-=s/c+1;
		s-=1ll*c*(s/c+1);
	}
	if(s<0 && c<0){
		for(int i=1;i<=n;i++) ans[i]-=-s/-c+1;
		s-=1ll*c*(-s/-c+1);
	}
	//cout<<"s="<<s<<endl;
	//for(int i=1;i<=n;i++) printf("%lld ",ans[i]); puts("");
	if(s==0){
		puts("Yes");
		for(int i=1;i<=n;i++) printf("%lld ",ans[i]); puts("");
		return;
	}
	if(s>0){
		ll t=0;
		for(int i=n;i;i--){
			t+=a[i];
			//cout<<i<<" "<<t
			if(t==-1){
				pd=1;
				for(int j=i;j<=n;j++) ans[j]+=s;
				break;
			}
		}
	}
	if(s<0){
		ll t=0;
		for(int i=n;i;i--){
			t+=a[i];
			if(t==1){
				pd=1;
				for(int j=i;j<=n;j++) ans[j]-=s;
				break;
			}
		}
	}
	if(!pd) puts("No");
	else{
		puts("Yes");
		for(int i=1;i<=n;i++) printf("%lld ",ans[i]); puts("");
	}
}
int main()
{
	//srand(time(0));
	//freopen("1.in","r",stdin);
	//freopen("1.out","w",stdout);
	int T=1; while(T--) work();
	return 0;
}

D

考虑数位dp，关键在于记什么样的状态，当时灵光一闪想到只需要记有多少个数进位的时候，还觉得自己挺nb的！现在想想也就这么回事，因为考虑的是进位的状态，而暴力的做法是直接枚举x，然后对于最小的i位，如果只关心是否进位，那就相当于n个数把\(10^i\)范围内的x分成了至多n个区间，区间内是等价的。于是只需记录多少个进位，然后将n个数按照$ \mod 10^i $排序，就知道哪些数有进位了。
第一发DP数组两维大小开反，ATC上是WA而不是RE，迷茫了15min，所幸最后发现了。。。

点击查看代码

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+5;
int n,a[N],pw[N],f[11][N];
int M;
bool cmp(int u,int v){
	return u%M>v%M;
}
void Min(int& x,int y){
	if(y<x) x=y;
}
void work(){
	cin>>n;
	pw[0]=1; for(int i=0;i<10;i++) pw[i+1]=pw[i]*10;
	for(int i=1;i<=n;i++){
		scanf("%lld",&a[i]);
	}
	memset(f,0x3f,sizeof(f));
	f[0][0]=0;
	for(int i=0;i<10;i++){
		M=pw[i];
		sort(a+1,a+n+1,cmp);
		
		int c[11]={0};
		for(int j=1;j<=n;j++) c[a[j]/M%10]++;
		for(int j=0;j<=n;j++){
			//cout<<i<<" "<<j<<" "<<f[i][j]<<endl;
			if(j) c[a[j]%(M*10)/M]--,c[a[j]%(M*10)/M+1]++;
			for(int x=0;x<10;x++){
				int s=0,u=0;
				//for(int k=10-x;k<=10;k++) s+=c[k];
				for(int k=0;k<=10;k++){
					u+=(k+x)%10*c[k];
					s+=(k+x)/10*c[k];
				}
				Min(f[i+1][s],f[i][j]+u);
			}
		}
	}
	//int ans=1e9;
	//for(int j=1;j<=n;j++) ans=min(ans,f[9][i]);
	cout<<f[10][0]<<endl;
}
signed main()
{
	//srand(time(0));
	//freopen("1.in","r",stdin);
	//freopen("1.out","w",stdout);
	int T=1; while(T--) work();
	return 0;
}