矩阵分解

矩阵分解

1 非负矩阵分解【NMF】

参考链接：文本主题模型之非负矩阵分解(NMF) - 刘建平Pinard - 博客园 (cnblogs.com)

2 奇异值分解【SVD】

参考链接：【转载】奇异值分解(SVD)计算过程示例 - marsggbo - 博客园 (cnblogs.com)

　　试着解释一下SVD矩阵：在我看来，SVD是对数据进行有效特征整理的过程。
　　首先，对于一个m×n矩阵A，我们可以理解为其有m个数据，n个特征，（想象成一个n个特征组成的坐标系中的m个点），然而一般情况下，这n个特征并不是正交的，也就是说这n个特征并不能归纳这个数据集的特征。SVD的作用就相当于是一个坐标系变换的过程，从一个不标准的n维坐标系，转换为一个标准的k维坐标系，并且使这个数据集中的点，到这个新坐标系的欧式距离为最小值（也就是这些点在这个新坐标系中的投影方差最大化），其实就是一个最小二乘的过程。
　　进一步，如何使数据在新坐标系中的投影最大化呢，那么我们就需要让这个新坐标系中的基尽可能的不相关，我们可以用协方差来衡量这种相关性。A^T·A中计算的便是n×n的协方差矩阵，每一个值代表着原来的n个特征之间的相关性。
　　当对这个协方差矩阵进行特征分解之后，我们可以得到奇异值和右奇异矩阵，而这个右奇异矩阵则是一个新的坐标系，奇异值则对应这个新坐标系中每个基对于整体数据的影响大小，我们这时便可以提取奇异值最大的k个基，作为新的坐标，这便是PCA的原理。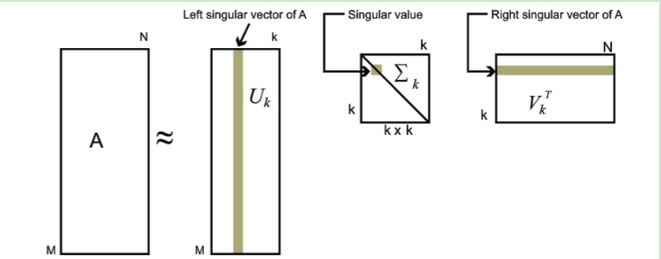

　　例如这个矩阵，先看k*k这个矩阵，寻找对角线上面的最大特征值，再找到最大特征值对应的左右矩阵上相应的位置代表的元素列。