[论文笔记] The Complexity of Andersen's Analysis in Practice

一个 context-insensitive 的 Andersen 风格的分析算法：

定义：

• \(N\) 是变量和 new 的总数量

• \(D(x)\) 是解引用变量 \(x\) 的 statements 数量

• \(G\) 是 flow graph

• \(E\) 是 flow graph 到达不动点时边的数量

定义：一个程序是 \(k-sparse\) 的当 \(max_xD(x) \leq k\) 且 \(E \leq kN\)

引理：对于 flow graph 中的某个 \(o_i\)（使用位置抽象对对象进行建模） 和 \(p\)，DoAnalysis 最多有一次满足 \(n = p \land o_i \in pt_{\Delta}(p)\) 的执行

理解：每个 \(o_i\) 只会进入 \(pt_{\Delta}(p)\) 一次，然后被加入 \(pt(p)\) 中

DoAnalysis 会做下面四个动作：

• 初始化：处理代码中所有的 x = new T() 和 x = y 调用，为 \(G\) 添加初始结点和初始边。

• 添加与 \(o_i\) 相关的边：处理字段访问和修改 x.f = y x = y.f。

• 传播：DiffProp。

• 清空 \(pt_{\Delta}(p)\)，把所有的新 \(o_i\) 转移到 \(pt(p)\) 中。

假设集合满足：(1) 常数时间检查元素是否存在 (2) 常数时间添加一个元素 (3) 常数时间的迭代；图类似

那么对于上面的四个动作：

• 初始化：对于 1-3 行，时间复杂度显然是 \(O(N)\)；对于 4-5 行，考虑任意两个变量之间都可能存在一个约束关系，所以复杂度是 \(O(N^2)\)

• 添加与 \(o_i\) 相关的边：if n represents x，所以考虑每一个解引用 x 的位置，之前被定义为 \(D(x)\)，\(|pt(x)|\) 是 \(O(N)\) 的，\(x\) 可以是任意一个变量，同样是 \(O(N)\) 的，那么添加边 y -> oi.f 直到图 \(G\) 的不动点这个动作的复杂度是 \(O(N^2max_xD(x))\)

引理：对于每个 flow graph 上的结点 \(p\)，在任意时刻都满足 \(pt(p) \cap pt_{\Delta}(p) = \emptyset\)

引理：对于一条边 \(e = n \rightarrow n'\)，对象 \(o_i\) 只会传播一次

• 传播：根据上面的引理，传播的时间复杂度显然是 \(O(NE)\)

• 清空 \(pt_{\Delta}(p)\)：每个对象在每个变量的 \(\Delta\) 集合中最多只能被清空一次，因此时间复杂度为 \(O(N^2)\)

综上所述，算法的时间复杂度上界为 \(O(N^2max_xD(x) + NE)\)，如果程序是 \(k-sparse\) 的，时间复杂度会退化成 \(O(kN^2)\)。之所以引入 \(k-sparse\) 的概念，是因为真实的 Java 程序很可能是 \(k-sparse\) 的。

Java 中类和方法的普遍结构决定 \(max_xD(x)\) 往往不会随着程序规模的增长而增长。\(G\) 的边 \(E\) 由赋值语句和对象上的字段访问语句引入。赋值语句显然是线性 \(O(N)\) 的。对象上的字段访问如果只使用 getter 和 setter 方法，那么每个对象仅有两个字段访问语句，Java 程序中对象上的字段数量是常数级别的，对象上的字段访问语句那么也是 \(O(N)\) 的。

当然，当字段是数组时数量就不再是线性的。在通过字段进行方法调用时，动态分派也可能导致流图边呈二次增长。

并行化和拓扑顺序可以加快传播速度，减少 worklist 的迭代次数。

实时构建调用图利用 receiver 的 points-to 集合推断可能的虚拟调用目标；把新发现的调用目标加入求解过程中。如果不考虑约束生成的成本，实时调用图推理会使分析变慢，因为达到不动点需要更多迭代。然而，如果将约束生成成本计入，实时调用图构建实际上提升了性能，因为不需要为不可达的库代码生成约束。

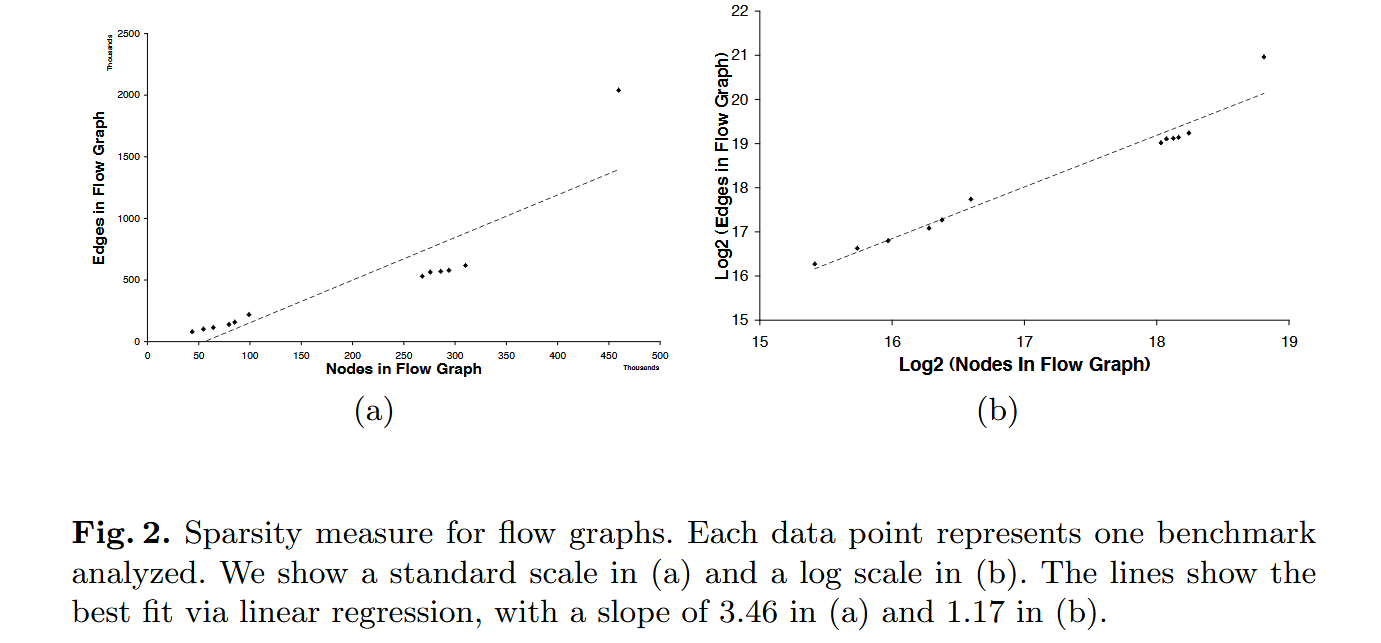
\(E = 3.46N\)

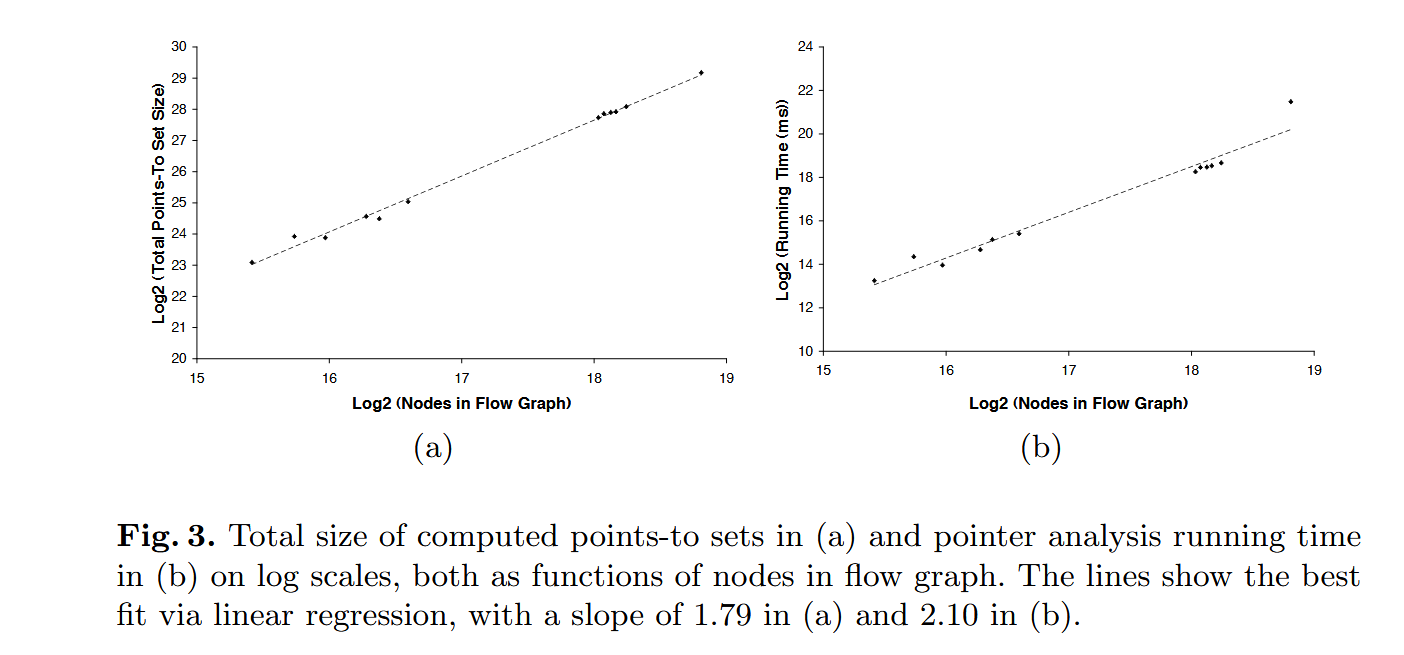
\(T = 2.10N\)