[论文笔记] Combining Formal and Informal Information in Bayesian Program Analysis via Soft Evidences

Background Information

摆了两三天觉得不能再开摆了，感觉至少把什么是贝叶斯方法及其名词搞懂（虽然可能概率论学过，但是已经忘干净了）：

贝叶斯的思考方式：先验概率 \(\pi(\theta)\) + 样本信息 \(X\) -> 后验概率 \(\pi(\theta | X)\) 不断根据新的证据更新我们的信念

事件 \(A\)：样本空间 \(\Omega\) 上的一个子集

概率 \(P\)：某个事件发生的概率，可以看作 \(\Omega\) 的子集到区间 \([0, 1]\) 的一个函数：\(2^{\Omega} \rightarrow [0, 1]\)，且满足规范性、非负性、有限可加性

随机变量 \(X\)：定义在样本空间上的函数，可以看作样本空间到数学空间的一个映射，对于抛硬币问题，\(\{正面, 反面\}\) 可以被映射为 \(\{0, 1\}\) 引入随机变量为了用实数来简化表达原来的样本空间，有个不太理解的点，随机变量的既然是个函数，“取值”又是怎么定义的呢（\(X\) 满足对任意取值 \(x\) \(\{\omega | X(\omega)\ <= x\} \in F\)）感觉还需要好好地学习一下概率论

条件概率（后验概率）：事件 A 在事件 B 发生的情况下发生的概率 记作 \(P(A|B)\)

联合概率：事件 A 和事件 B 同时发生的概率 记作 \(P(A, B)\) \(P(AB)\) \(P(A \cap B)\)

边缘概率（先验概率）：事件 A 发生的概率 记作 \(P(A)\)

\(P(A|B) = \frac{P(AB)}{P(B)}\)

根据条件概率的定义可以推出 \(P(A|B) = \frac{P(B|A)P(A)}{P(B)}\)

对于随机变量的定义类似

使用一组随机变量 \(\{X_1, X_2, ..., X_n\}\) 刻画事件，把问题表示为一个联合概率分布 \(P(X_1, X_2, ..., X_n)\)，假设对于一个 \(X_i\) 存在一个随机变量的子集 \(\pi(X_i)\)，使得 \(X_i\) 与不属于该子集的所有随机变量相互（边缘）独立，那么 \(P(X_i|X_1, X_2, ..., X_{i-1}) = P(X_i|\pi(X_i))\)，即（根据链规则） \(P(X_1, X_2, ..., X_n) = \Pi P(X_i|\pi(X_i))\)，可以根据 \(\pi(X_i)\) 对随机变量刻画一组边结构

贝叶斯网络的有向无环图中的结点 \(V\) 表示随机变量，有向边 \(E\) 表示条件概率，假设有边 \((X, Y)\) 那么权重为 \(P(Y|X)\)

不同的随机变量顺序会导致不同的网络结构，建议用因果关系

既然已经把随机变量之间的关系用图来刻画，那么可以用图的方法描述随机变量之间的关系，随机变量之间的关系对应图上结点的分隔，可以被划分为三种形式：

• 顺连：如果 \(Z\) 未知，那么 \(X\) 会影响 \(Z\)，从而间接影响 \(Y\)，这个比较好理解

• 分连：还不太理解

• 汇连：还不太理解

阻塞：根据顺连、分连、汇连划分为三种，如果一个节点的集合 \(Z\) 阻塞了 \(X\) 和 \(Y\) 之间的所有通路，那么就说 \(Z\) 有向分隔（d-分隔） \(X\) 和 \(Y\)。如果 \(Z\) 有向分隔 \(X\) 和 \(Y\)，那么在 \(Z\) 确定时，\(X\) 和 \(Y\) 条件独立。

Introduction

soft evidence：不确定的观测信息，反映概率性观测

soundness：程序分析是否能够捕获程序的所有行为（实际上学术界和工业界的分析工具/分析方法都是 unsound 的，所以还有一个 soundy/soundiness 的概念）

三个问题：

• 怎么把 soft evidence 和现有的分析工具/分析方法合并而不破坏其 soundness？

• 怎么自动化地进行上面的合并？

• 怎么提取 soft evidence？

方法：提出了一种 neural-network 的方法来解决上面的问题：

• 在现有的使用 Datalog 的分析工具中引入概率信息（Problog），把传统的逻辑分析方法转换成贝叶斯模型，soft evidence 会逐步增加对于某个证据的信心，但是不会破坏分析能够捕获的行为（只是排了个序）

• 引入神经网络来判别程序中 informal facts 的可能性，并将其输出编码成 soft evidence 给贝叶斯模型使用。

结果很有效

Overview

有一个例子：一个 Java 代码及一个 Datalog 实现的指针分析

显然 R1 对应的类型转换是安全的，R2 对应的类型转换是不安全的

一开始没太细看这个 Datalog，发现例子看不懂了，还是要看一下：

pointsTo(V, H) :- allocation(V, H)

内存分配对应指针指向，V 和 H 分别代表变量和堆（对堆建模后的一个结果？）

pointsTo(V, H) :- move(U, V), pointsTo(U, H)

如果存在两个指针间的赋值关系，认为他们指向同一个对象

fieldPointsTo(H1, F, H2) :- putField(V, F, U), pointsTo(V, H1), pointsTo(U, H2)
pointsTo(U, H2) :- getField(V, F, U), pointsTo(V, H1), fieldPointsTo(H1, F, H2)

如果给变量 V 的字段 F 赋值变量 U，且 V 和 U 分别指向对象 H1, H2，那么认为 H1 的字段 F 指向 H2；取出字段类似

unsafeDowncast(L) :- downcast(L, T1, V), pointsTo(V, H), typeOf(H, T2), !subType(T2, T1)

不安全的类型转换，如果位置 L 上存在一个类型转换从变量指向的对象的原类型 T2 转换到 T1，且 T2 不是 T1 的子类型，那么这个类型转换是不安全的

• 流不敏感：不考虑语句的执行顺序

• 上下文不敏感：不考虑运行时上下文

在流不敏感和上下文不敏感，但是字段敏感的前提下，这个指针分析会给出两个不安全的类型转换：unsafeDowncast(9) 和 unsafeDowncast(17)，显然 9 是个误报，为了解决这个误报，不得不使这个指针分析变得流敏感，这个开销就有点大了

但是对于人类程序员来说，类型转换的正确性是很容易被“猜测”的（作为一个证据有一定的置信度），dog 转到 animal 看上去就很行（dog is an animal），dog 转到 dolphin 看上去就不太行（dog is not a dolphin）。

首先把这个 Datalog 转成 Problog，通过上面的例子发现取出字段的规则是造成误报的原因（流不敏感），因此把它的置信度调成 0.9

为了合并 informal information，需要添加一个新的规则。通过上面的例子引入一个 ailas 规则，置信度也给 0.9：

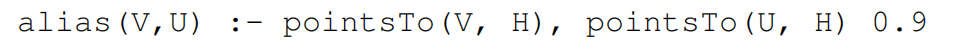
使用 GraphCodeBert + 微调（2 层全连接）判断 ailas 作为 soft evidence 的可信度，alias(dolphin, dog1) 是 0.79。传统方式（当作 hard evidence）是设置一个阈值（比如 0.5），超过阈值的认为它是一个 positive evidence，否则 negative evidence。但是这个阈值是很 tricky 的。

• noisy sensors：“具备噪声的传感器”，指的是那些可能产生不准确或不完全观测结果的设备或机制，结果并非完全可信

virtual evidence 是 soft evidence 的一种应用形式，在贝叶斯网络中引入一个虚拟结点 'alias

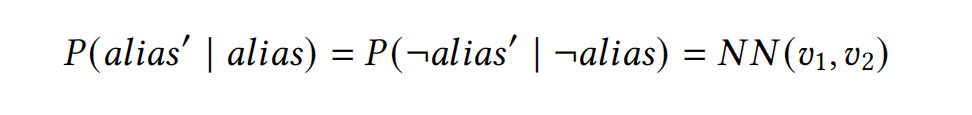
因为不懂贝叶斯网络和概率编程，所以不太理解 alias 是怎么起作用的，为什么要引入 virtual evidence 和条件概率。先继续看吧。

Preliminaries

介绍了一下概率程序 probabilistic program 的文法和语义：

文法比较简单。

一个概率程序定义了一组 Datalog 程序的分布，Datalog 程序又定义了 Datalog 输出的分布。可以通过采样过程定义 Datalog 程序的分布。具体来说，首先，一个 probabilistic rule 会通过把变量替换为所有可能的值被转换成一组 ground probabilistic rule，使用 \(\sigma\) 表达这种转换。为了简化，我们推广 \(\sigma\) 使其也可以指代完成转换后的某个规则。使用 \(U_{\overline{c}_p}\) 指代从某个概率程序得到的所有 ground probabilistic rule。其次，根据概率从 \(U_{\overline{c}_p}\) 中采样一个子集 \(PGC\)，这个子集的整体概率被定义为 \(P_{[[\overline{c}_p]]}_{\omega}(PGC)\)。但是，我们还要考虑 evidences（某些子集程序是不能满足 evidence 的）。简单来说，一个子集程序的概率为 0 当它不能推导出元组 t 当观测到元组 t（即 \(observe(t)\)）。其他满足证据的子集程序的概率需要被 re-normalized。使用 \([[\overline{pgc}]]_D\) 指代确定性地计算一组 probabilistic rules，就是计算其对应的 Datalog（抛弃掉概率）。对于一个概率非 0 的子集程序，它的概率将和所有概率非 0 的子集程序们一起正则化。最终，一组元组 \(T\) 的概率通过加上所有能推理出 \(T\) 的子集程序的概率来得到，使用 \(P_{[[(\overline{c}_p, \overline{e})]]_w(T)}\) 来指代这个概率。对于一个元组 \(t\) 的边缘概率 margin 可以通过累加所有包含 \(t\) 的 \(T\) 的概率得到。

这段符号有点乱飞了（可能是我太菜），但是仔细看是看得懂的。简单来说，概率程序把 Datalog 语句（就是 rule）看作样本。感觉还是没太理解到符号使用的精髓，先放着吧。对贝叶斯网络也没什么理解说是。

Overall Framework

分为 Offline 和 Online 两部分，Offline 关注训练，Online 关注推理。

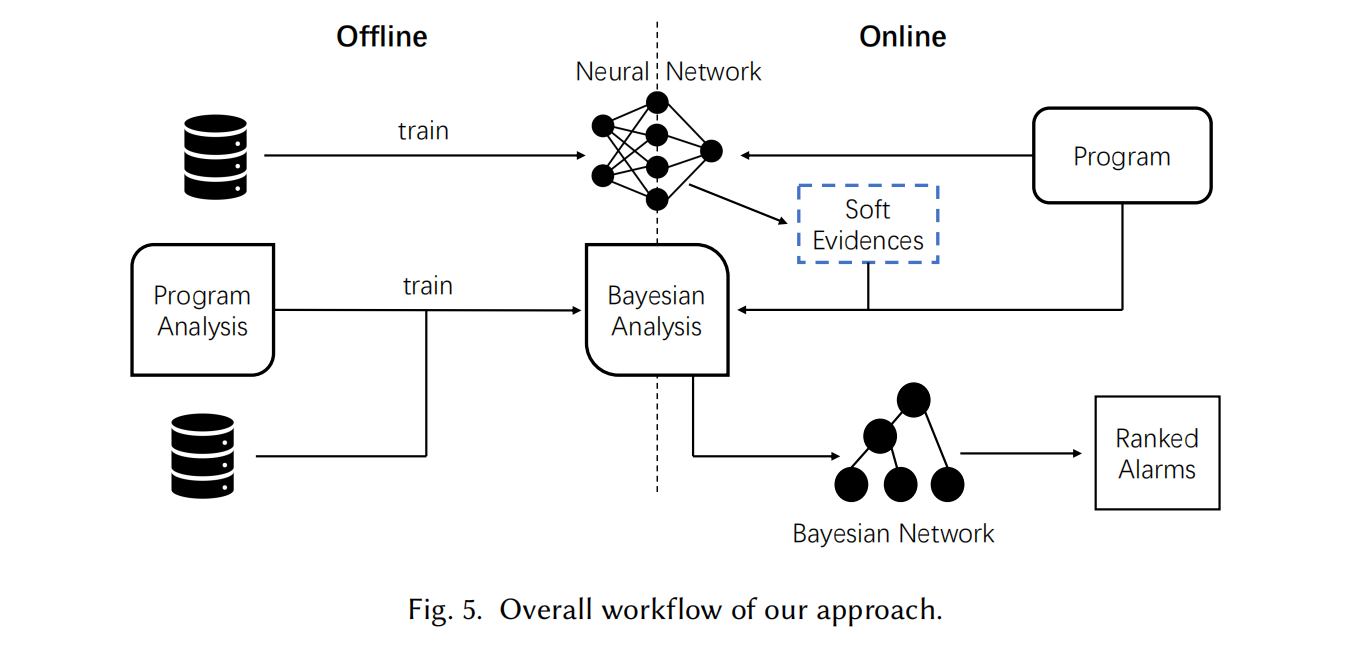
Online Inference With Soft Evidence

算法的输入包括一个贝叶斯程序分析 \(pa\)、一个待分析的程序 \(T\)、一个关系 \(r(\bar{v})\)（其元组将通过软证据进行观察）以及一个神经网络 \(NN\)，用于为关系 \(r(\bar{v})\) 中的每个程序事实提供软证据，从而指示其成立的可能性。

Definitions of Soft Evidences

• \(Odds\)：对于事件 \(\beta\) 发生相对于其不发生的信心

• soft evidence：\(observe(\beta) \ k\)，\(Odd\) 会增长 \(k\) 倍当观测到一次 \(\beta\)

但是神经网络不会产出关键参数 \(k\)，而是直接产出条件概率

Encoding Soft Evidences using Conditional Probabilities

soft evidence 可以看作是对某个事件的 noisy sensor。soft evidence 不一定可靠，所以引入一个事件 \(t'\) 表示 soft evidence 的看法。事件 \(t'\) 是对事件 \(t\) 的一种观测。

从 Bayes Factor \(k\) 导出两个条件概率：

Compiling into a Bayesian Network

尝试了 Problog 的推理引擎，但是在这个实验的数据集上未能终止。所以选择了 Bingo 这个工作的方法，通过把贝叶斯分析转换成贝叶斯网络得到一个近似的分析结果（\(\pi(X_i)\) 贝叶斯网络可以提高效率）。“近似”是因为贝叶斯网络是一个有向无环图，分析推导过程中可能出现循环依赖，使用 Bingo 方法消除分析环路将导致结果近似。

添加两个条件概率：

1. 对于一个元组 \(t\)，如果所有的 ground probabilistic rule 都不能推导出它，那么它的概率为 0；有一些可以推导出它，那么它的概率为 1

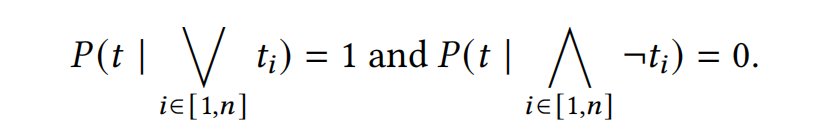
2. 对于一个 rule，对于组成它的 body 的元组，所有元组都成立时，rule 的概率为 p（添加的概率），有任意一个元组不成立时，rule 的概率为 0

然后把 soft evidence 加入到贝叶斯网络中，最后计算边缘概率。

Offline learning

Generating a Bayesian Program Analysis

关键是给原来的 Datalog 中的每一个 rule 指派一个概率。可以通过有标签的数据来训练。使用 expectation-maximization 算法。

基于非正式信息直接对分析结果提供额外信息会比较困难，但对从分析结果进一步推导出来的事实提供信息可能会更容易。在这种情况下，需要为分析添加额外的规则以推导这些事实。新增规则的近似性应该与原始分析保持一致：如果原始分析是过近似的（may analysis），那么新增规则也应该是过近似的。如果原始分析是欠近似（must analysis）的，新增规则也应该保持欠近似。

Training a Neural Network Output to Produce Soft Evidences

用极大似然估计训练神经网络

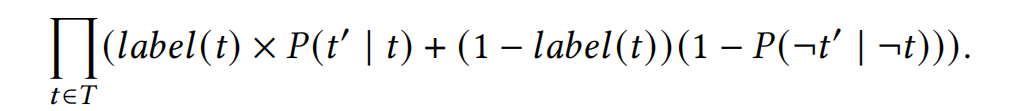
假设 \(P(t' | t) = P(\neg t' | \neg t)\) 简化训练目标。用预训练的网络提取嵌入向量，在嵌入向量后用神经网络做微调。