[翻译] Type Systems —Luca Cardelli

GPT-4o-mini 翻译，经个人审校。添加了一点笔记。

原文地址 Type Systems

Introduction

类型系统的基本目的是避免程序运行过程中出现运行错误。这个不够正式的说法激励了对类型系统的研究，但是还需要更进一步的澄清。这个说法的准确性首先依赖于一个相当微妙的问题，即什么构成运行错误，我们将对此进行详细探讨。即使这个问题得到解决，要程序运行中不发生错误仍然是一个复杂的特性。当这种特性在某个编程语言可以表达的所有程序中都成立时，我们称该语言为类型安全的。实际上，为了避免对编程语言的类型安全性做出错误或模棱两可的声明，进行细致的分析是必不可少的。因此，类型系统的分类、描述和研究逐渐发展成为一门正式的学科。

为了形式化类型系统，要求给出精确的符号和定义，以及形式性质的详细证明，以确保定义的合理性。有时，这一学科会变得相当抽象。但是应该始终铭记，核心动机是实用性的：这些抽象概念是出于实用要求而产生的，通常可以直接与具体的直觉相联系。此外，形式化技术并不需要完全应用才能发挥其作用和影响。掌握类型系统的主要原则能够帮助我们避免显而易见或不易察觉的陷阱，同时还能在语言设计中激发可复用和解耦的特性。

当类型系统被正确设计时，它可以作为一种工具，用来评估编程语言定义中关键部分是否足够完善。相反，非正式的语言描述往往无法清晰地定义语言中类型的结构，这会导致实现时出现模糊性。同一语言的不同编译器可能会实现略有不同的类型系统。此外，有些语言的定义存在类型不安全的问题，即程序虽然通过了类型检查（type checker），但运行时仍可能崩溃。理想情况下，形式化的类型系统应该成为所有类型化编程语言定义的一部分。这样，类型检查算法就可以根据明确的规范进行验证，而整个语言也有可能被证明是类型安全的，从而避免潜在的问题。

在这一节中，我们会提出一套关于类型、执行错误及相关概念的非正式术语。我们将讨论类型系统的预期特性和优势，并回顾类型系统如何进行形式化定义。引言中使用的术语并非完全标准，这主要是由于来源不同而导致的标准术语存在不一致性。通常情况下，我们避免在描述运行时相关概念时使用“类型”和“类型化”这样的词汇。例如，我们用“动态检查”替代“动态类型”，并避免使用诸如“强类型”这样常见但含糊不清的术语。这些术语的定义将在“术语定义”部分中进行总结。

第2节中，我们解释了描述类型系统时常用的符号表示法。我们回顾了判断（judgments），即关于程序类型的形式化断言；类型规则（type rules），即判断之间的推理关系；以及推导（derivations），即基于类型规则进行的演绎过程。第3节中，我们回顾了一系列简单类型，这些类型的类似概念可以在常见编程语言中找到，并详细说明了它们的类型规则。第4节中，我们展示了一种简单但完整的命令式语言的类型规则。第5节中，我们讨论了一些高级类型构造的类型规则，包括多态性和数据抽象。第6节中，我们解释了如何通过引入子类型概念来扩展类型系统。第7节是对一些我们未详细讨论的重要主题的简要评论。第8节中，我们探讨了类型推断问题，并介绍了针对主要类型系统的类型推断算法。最后，第9节总结了研究成果并展望了未来的发展方向。

note: 引言部分

Execution errors

程序运行错误（execution error）最明显的表现是出现意外的软件错误，例如非法指令错误或非法内存引用错误。然而，还有一些更为隐蔽的执行错误会导致数据损坏，但不会立刻表现出明显的症状。此外，还有一些软件错误（例如除以零或解引用空指针）通常并不会被类型系统所检查出来并防止其发生。最后，也存在一些缺乏类型系统的语言，但在这些语言中软件错误并未发生。因此，我们需要谨慎地定义相关术语，从“什么是类型”这一问题开始。

Typed and untyped languages

程序变量在程序执行期间可以取一系列的值，值域的上界称为该变量的类型。例如，一个类型为布尔（Boolean）的变量 \(x\)，在程序的每次运行中都应该仅取布尔值。如果 \(x\) 的类型是布尔，那么布尔表达式 \(\text{not}(x)\) 在程序的每次运行中都具有合理的意义。能够为变量赋予（非平凡）类型的语言称为类型化语言（typed languages）。

note: 此处的上界我理解是在格上的上界，比如布尔型的 true 和 false 的上界应该是 {true, false}，是两个取值的并集，也是二者在格上的最小上界，然后我们认为这个集合是“布尔型”这个名词

不限制变量取值范围的语言被称为无类型语言（untyped languages）：它们没有类型，或者等价地说，它们只有一个包含所有值的单一通用类型。在这些语言中，操作可能会被应用于不适当的参数，其结果可能是一个固定的任意值、一个错误（fault）、一个异常（exception），或者一个未定义的效果（unspecified effect）。纯 \(\lambda\)-演算（pure \(\lambda\)-calculus）是无类型语言的一个极端例子，其永远不会发生错误：因为唯一的操作是函数应用，而由于所有值都是函数，所以该操作永远不会失败。

类型系统（type system）是类型化语言中的一个组成部分，用于追踪变量的类型，以及通常情况下，程序中所有表达式的类型。类型系统被用来判断程序是否表现良好（这一点将在后续讨论）。只有符合类型系统的程序源代码才应被视为类型化语言的真正程序；不符合类型系统的源代码应在运行之前被抛弃掉。

一门语言之所以被称为类型化语言，是因为它具有一个类型系统，而不论类型是否实际出现在程序的语法中。如果类型是语法的一部分，则称为显式类型化（explicitly typed）；否则称为隐式类型化（implicitly typed）。目前没有主流语言是纯粹隐式类型化的，但诸如 ML 和 Haskell 等语言支持在大范围的程序片段中省略类型信息；这些语言的类型系统会自动为这些程序片段分配类型。

Execution errors and safety

在程序执行过程中，可以将错误分为两种类型：一种是会导致计算立即停止的错误，另一种是暂时未被察觉（可能持续一段时间），最终导致程序出现不可预测行为的错误。前者称为可捕获错误（trapped errors），而后者称为不可捕获错误（untrapped errors）。

一个典型的不可捕获错误的例子是对合法地址的不当访问，例如在缺乏边界检查的情况下访问数组末尾之后的数据。另一个可能长时间未被发现的不可捕获错误是跳转到错误的地址：该地址上的内存可能表示指令流，也可能不表示。相比之下，可捕获错误的例子包括除以零和访问非法地址：在许多计算机架构上，这些错误会导致计算立即停止。

如果一个程序不会导致不可捕获错误（untrapped errors）的发生，则称该程序是安全的（safe）。产生的所有程序均安全的语言被称为安全语言（safe languages）。因此，安全语言排除了运行错误中最隐蔽的形式：那些可能暂时未被察觉的错误。无类型语言（untyped languages）可以通过运行时检查来强制实现安全性，而类型化语言则可以通过静态检查来拒绝所有潜在不安全的程序。此外，类型化语言也可能结合运行时检查和静态检查来实现安全性。

尽管安全性是程序的重要属性，但很少有类型化语言仅关注消除不可捕获错误。类型化语言通常还试图排除大量的可捕获错误（trapped errors），以及不可捕获错误。接下来我们将讨论这些问题。

note: 把类型化和安全/不安全看作独立的部分，也就是说，暂时忘掉类型化

Execution errors and well-behaved programs

对于任意一种语言，我们将所有可能出现的执行错误划分出一个子集，称为禁止错误（forbidden errors）。禁止错误应包括所有的不可捕获错误（untrapped errors）以及可捕获错误（trapped errors）的子集。如果一个程序片段不会导致任何禁止错误的发生，则称该程序片段具有良好行为（good behavior），或者等价地称其为行为良好（well behaved）。相反，若程序片段导致禁止错误的发生，则称其具有不良行为（bad behavior），或者等价地称其为行为不良（ill behaved）。特别地，一个行为良好的程序片段是安全的（safe）。如果某种语言的所有（合法）程序都具有良好行为，则称该语言是强检查的（strongly checked）。

因此，对于给定的类型系统，以下性质适用于强检查语言：

• 不会发生不可捕获错误（安全性保证）。
• 不会发生被指定为禁止错误的可捕获错误。
• 其他可捕获错误可能会发生，此时避免这些错误的责任由程序员自行承担。

类型化语言可以通过静态检查（即编译时检查）来强制实现良好行为（包括安全性），从而防止不安全或行为不良的程序被执行。这类语言被称为静态检查语言（statically checked languages）。检查过程称为类型检查（typechecking），执行该检查的算法称为类型检查器（typechecker）。通过类型检查器的程序被称为良类型的（well typed），否则被称为类型不良（ill typed）。类型不良可能意味着程序实际上具有行为不良，也可能只是表示无法保证其行为良好。静态检查语言的典型例子包括 ML、Java 和 Pascal（需要注意的是，Pascal 存在一些不安全的特性）。

非类型化语言可以通过另一种方式来强制实现良好行为（包括安全性），即执行足够详细的运行时检查（run-time checks），以排除所有禁止错误。例如，这些语言可能会检查所有数组边界以及所有除法操作，并在禁止错误即将发生时生成可恢复的异常。这种语言中的检查过程称为动态检查（dynamic checking）。LISP 是这种语言的一个典型例子。尽管这些语言既没有静态检查，也没有类型系统，它们仍然可以被称为强检查的（strongly checked）。

即使是静态检查的语言，通常也需要在运行时执行某些测试以确保安全性。例如，数组边界通常必须通过动态检查来验证。一个语言是静态检查的，并不意味着程序的执行可以完全“盲目”进行。

一些语言利用其静态类型结构来实现复杂的动态测试。例如，Simula67 的 INSPECT、Modula-3 的 TYPECASE 和 Java 的 instanceof 构造能够根据对象的运行时类型进行区分。尽管如此，这些语言仍然（稍显不准确地）被认为是静态检查的语言，部分原因是这些动态类型测试是基于静态类型系统定义的。换句话说，用于类型相等的动态测试与类型检查器在编译时用于确定类型相等性的算法是兼容的。这种兼容性使得动态测试与静态类型系统保持一致，从而支持静态检查语言的安全性和灵活性。

note: 区分可捕获错误/不可捕获错误和禁止错误/非禁止错误，区分安全/不安全和良好行为/不良行为，程序语言期望保证程序的良好行为

Lack of Safety

根据我们的定义，一个行为良好的程序是安全的。安全性是一种更基础且更重要的属性，甚至比良好行为更为重要。类型系统的主要目标是通过排除所有程序运行中的不可捕获错误来确保语言的安全性。然而，大多数类型系统的设计目标是确保更广泛的良好行为属性，并隐含地保证安全性。因此，类型系统的声明目标通常是通过区分类型正确的程序与类型错误的程序来确保所有程序的良好行为。

实际上，某些静态检查语言并不能完全确保安全性。这意味着，这些语言的禁止错误未涵盖所有的不可捕获错误。这些语言可以被委婉地称为弱检查语言，即某些不安全操作能够被静态检测到，而某些则不能。属于这一类的语言之间在其“弱检查”程度上差异也很大。例如，Pascal 只有在使用未标记的变体类型和函数参数时才会变得不安全；而 C 则有许多不安全且被广泛使用的特性，例如指针运算和类型转换。有趣的是，C 程序员的“十诫”中前五条都是为了弥补 C 的弱检查特性所带来的问题。C++ 对 C 中的一些弱检查问题进行了缓解，而 Java 更进一步解决了更多问题，这表明编程语言正在逐渐远离弱检查的趋势。此外，Modula-3 支持不安全特性，但仅限于那些明确标记为“不安全”的模块，并且禁止安全模块导入不安全接。这种设计进一步强化了语言的安全性，同时允许在需要时使用不安全的功能。

大多数无类型语言出于必要性，实际上是完全安全的（例如，LISP）。否则，如果既没有编译时检查也没有运行时检查来防止数据的损坏，那么编程将变得极其困难。相比之下，汇编语言属于令人不快的无类型且不安全的语言。

note: 语言的安全与否是可以通过严格的设计解决的

Should languages be safe?

一些编程语言（如 C）由于性能方面的考虑，刻意设计得不够安全：为了实现安全性所需的运行时检查，有时被认为代价过高。即使是在进行广泛静态分析的语言中，安全性也有其成本：例如，数组边界检查这样的测试通常无法在编译时完全消除。

尽管如此，人们仍然进行了许多尝试，设计出 C 的一个安全子集，并开发工具，通过引入各种（相对高成本的）运行时检查来尝试安全地执行 C 程序。这些尝试主要出于两个原因：一是 C 被广泛应用于对性能要求不高的场景，二是由不安全的 C 程序引发的安全问题。这些安全问题包括由于指针运算或缺乏数组边界检查而导致的缓冲区溢出和下溢，这些问题可能导致任意内存区域被覆盖，并可能被利用来发动恶意攻击。

安全性从多种衡量标准来看是具有成本效益的，而不仅仅是纯粹的性能考量。安全性在发生执行错误时能够产生失败终止行为（fail-stop behavior），从而缩短调试时间。安全性可以保证运行时结构的完整性，因此支持垃圾回收（garbage collection）。反过来，垃圾回收虽然牺牲了一定的性能，却显著减少了代码规模和开发时间。此外，安全性已经成为系统安全的必要基础，尤其是对于那些需要加载并运行外部代码的系统（如操作系统内核和网页浏览器）。系统安全正日益成为程序开发和维护中最昂贵的方面之一，而安全性可以帮助降低这类成本。

因此，在选择使用安全语言还是不安全语言时，最终可能需要在开发与维护时间和执行时间之间进行权衡（trade-off）。尽管安全语言已经存在了数十年，但直到最近由于安全问题的日益突出，它们才逐渐成为主流选择。这种转变主要是因为安全性已经成为现代系统设计中不可忽视的关键需求。

Should languages be typed?

关于编程语言是否应该具有类型系统的问题仍然存在争议。然而，对于代码的生产而言，用无类型语言编写的代码在维护上毋庸置疑会极为困难。从可维护性的角度来看，即使是弱类型检查的不安全语言，也优于安全但无类型的语言（例如，C 相对于 LISP）。以下是从软件工程角度出发，支持类型化语言的主要论点：

• 执行的高效性：类型信息最初被引入编程中是为了改进代码生成和数值计算的运行时效率，例如在 FORTRAN 中。在 ML 中，精确的类型信息消除了对指针解引用时进行空值检查的需求。通常来说，在编译时提供精确的类型信息，可以在运行时直接应用适当的操作，而无需进行昂贵的测试。

• 小规模开发的高效性。当一个类型系统设计良好时，类型检查可以捕获大量常见的编程错误，从而避免冗长的调试过程。实际发生的错误也更容易调试，因为大类的其他错误已经被排除。此外，有经验的程序员会采用一种编码风格，使某些逻辑错误表现为类型检查错误：他们将类型检查器作为一种开发工具。（例如，当某个字段的不变量发生变化时，即使其类型保持不变，也通过更改字段名称来触发错误报告，从而定位其所有旧的使用位置。）

• 编译的高效性。类型信息可以组织成程序模块的接口，例如在 Modula-2 和 Ada 中。模块可以彼此独立编译，每个模块仅依赖于其他模块的接口。这样，大型系统的编译效率得以提高，因为当接口保持稳定时，对某个模块的修改不会导致其他模块重新编译。

note: 类型信息可以帮助程序员确定模块间的接口

• 大规模开发的高效性。接口和模块在代码开发中具有方法论上的优势。大型团队的程序员可以协商要实现的接口，然后分别着手实现对应的代码部分。代码片段之间的依赖性被最小化，代码可以在局部范围内进行调整，而无需担心对全局产生影响。（虽然这些优势也可以通过非正式的接口规范来实现，但实际上，类型检查在验证对规范的遵守方面提供了极大的帮助。）

• 注重安全的应用领域中开发和维护的高效性。尽管安全性对于消除诸如缓冲区溢出之类的安全漏洞是必要的，但类型系统对于消除其他灾难性的安全漏洞同样不可或缺。以下是一个典型的例子：如果存在任何途径（无论多么复杂）可以将整数转换为指针类型（或对象类型）的值，那么整个系统就会被攻破。如果这种转换可能发生，攻击者就能够以任何类型查看数据，从而访问系统中任意位置的数据，即使是在其他方面受到类型语言约束的情况下。此外，还有一种常见但不必要的技术，即将一个类型化的指针转换为整数，再将其转换为另一种类型的指针，这也可能导致类似问题。在维护成本和整体执行效率方面，使用类型化语言是消除这些安全问题的最具成本效益的方法。然而，安全性是一个贯穿系统各个层次的问题：类型化语言提供了一个优秀的基础，但并不是完整的解决方案。

• 语言特性的高效性。类型构造能够自然地以“正交”的方式组合。例如，在 Pascal 中，数组的数组可以用来建模二维数组；在 ML 中，具有单个参数（该参数是包含 \(n\) 个元素的元组）的过程，可以用来建模具有 \(n\) 个参数的过程。因此，类型系统促进了语言特性的可扩展性，从而降低编程语言的复杂性。

note: 这里的“正交”指一个新的特性能被很自然的添加到一个语言中，而无需做出特别的适配或调整

Expected properties of type systems

在本章中，我们假设编程语言应该既安全又类型化，因此应当采用类型系统。在研究类型系统时，我们不区分“可捕获错误”和“不可捕获错误”，也不区分安全性和良好行为：我们专注于良好行为，并将安全性视为一种隐含的属性。

note: 良好行为的程序必定是安全的

类型，在编程语言中通常具有一些实际的特性，这些特性使它们区别于程序中的其他注解形式。一般来说，关于程序行为的注解可以从非正式的注释到需要定理证明的形式化方法，跨度非常大。类型处于这一范围的中间位置：它们比程序注释更精确，但比形式化方法更容易实现和操作。

以下是对所有的类型系统的基本预期属性：

• 类型系统应当是可判定验证的（Decidably Verifiable）：类型系统需要提供一个算法（称为类型检查算法），用来确保程序是良好行为的。类型系统的目的不仅仅是表达程序员的意图，还要在程序执行之前主动捕获可能的执行错误。（任意的正式规范通常不具备这种特性，因其可能需要复杂的定理证明，甚至不可判定。）

note: 就是说类型检查算法必须是可判定的

• 类型系统应当是透明的（Transparent）：程序员应该能够轻松预测程序是否可以通过类型检查。如果程序未能通过类型检查，失败的原因应该是显而易见的。（自动定理证明通常不具备这种透明性，因为其失败原因可能难以理解或追踪。）

• 类型系统应当是可强制执行的（Enforceable）：类型声明应尽可能在静态检查阶段验证；对于无法静态验证的部分，应在运行时动态检查。程序中的类型声明与其关联的代码之间的一致性应当被例行验证。（程序注释和编程约定通常无法强制执行这种一致性。）

How type systems are formalized

正如我们所讨论的，类型系统用于定义“良好类型化”（well typing）的概念，而良好类型化本身是良好行为（隐含安全性）的一种静态近似。安全性通过“失败停止行为”（fail-stop behavior）来简化调试过程，并通过保护运行时状态来实现垃圾回收。良好类型化进一步通过在运行时之前捕获执行错误，促进了程序的开发过程。

但是，我们如何保证良好类型化的程序确实是良好行为的呢？也就是说，我们如何确保一种语言的类型规则不会意外地允许不良行为的程序通过检查？

形式化的类型系统是对编程语言手册中所描述的非形式化类型系统的数学刻画。一旦类型系统被形式化，我们就可以尝试证明一个类型正确性定理（type soundness theorem），该定理声明良好类型化的程序具有良好行为。如果这样的正确性定理成立，我们就称这个类型系统是正确的（sound）。(一种类型化语言中所有程序的良好行为与其类型系统的正确性是同义的。)

为了形式化一个类型系统并证明其正确性，我们必须从本质上形式化整个语言。

形式化编程语言的第一步是描述其语法。对于大多数感兴趣的语言，这归结为描述类型和项的语法。类型表达程序的静态知识，而项（语句、表达式和其他程序片段）表达算法行为。

下一步是定义语言的作用域规则，这些规则明确地将标识符的出现与其绑定位置（即标识符声明的位置）关联起来。类型化语言所需的作用域规则通常是静态的，这意味着标识符的绑定位置必须在运行时之前确定。绑定位置通常可以仅通过语言的语法来确定，而无需进一步的分析；这种静态作用域被称为词法作用域。缺乏这种静态作用域则被称为动态作用域。

作用域可以通过形式化地定义程序片段的自由变量集合来指定（这涉及明确变量如何通过声明被绑定）。随后可以定义与之相关的类型或项对自由变量的“替换”概念。

当这些内容确定后，就可以进一步定义语言的类型规则。这些规则描述了一种形式为 \(M : A\) 的“具有类型”关系，其中 \(M\) 是项，\(A\) 是类型。一些语言还需要定义类型之间的“子类型”关系，形式为 \(A <: B\)，以及类型等价关系，形式为 \(A = B\)。语言的类型规则的集合构成了它的类型系统。具有类型系统的语言被称为类型化语言。

在正式化类型规则之前，必须引入另一个基础成分，这个成分并未直接体现在语言的语法中：静态类型环境。静态类型环境用于记录程序片段中自由变量的类型信息，在类型检查过程中，它与编译器的符号表紧密对应。类型规则总是相对于正在进行类型检查的程序片段的静态环境来制定的。例如，“具有类型”关系 \(M : A\) 是与一个静态类型环境 \(\Gamma\) 相关联的，这个环境包含关于 \(M\) 和 \(A\) 中自由变量的信息。完整的关系写作 \(\Gamma \vdash M : A\)，表示在环境 \(\Gamma\) 中，项 \(M\) 的类型为 \(A\)。

类型系统的基本概念几乎适用于所有编程范式（如函数式、命令式、并发式等）。具体的类型规则通常可以在不同的范式中保持不变。例如，关于函数的基本类型规则，无论语义是按名调用（call-by-name）还是按值调用（call-by-value），或者无论语言是函数式还是命令式，这些规则基本上都可以直接沿用。

在本章中，我们将独立于语义来讨论类型系统。然而，需要明确的是，最终类型系统必须与某种语义相关联，并且健全性（soundness）必须在该语义下成立。健全性确保类型系统的静态检查与程序的动态行为之间的一致性。值得一提的是，结构化操作语义（structural operational semantics）是一种能够统一处理多种编程范式的技术方法，与本章对类型系统的讨论非常契合。结构化操作语义提供了一种系统化的方式来描述程序的动态行为，从而为类型系统的健全性证明提供了坚实的基础。

Type equivalence

在大多数非平凡的类型系统中，通常需要定义一个类型等价关系（type equivalence），即判断两个类型表达式是否等价。这是定义编程语言时的一个重要问题：什么时候两个独立的类型表达式可以被认为是等价的？假设有两个不同的类型名称，它们分别被关联到相同的类型：

\(type X = Bool\)
\(type Y = Bool\)

如果类型名称 \(X\) 和 \(Y\) 因关联到相同的类型而匹配，我们称之为结构等价。如果它们因为类型名称不同而无法匹配（而不考虑关联的类型），我们称之为按名称等价。

在实际应用中，大多数编程语言都会混合使用结构等价和按名称等价。纯粹的结构等价可以通过类型规则轻松且精确地定义，而按名称等价则更难明确定义，其通常具有算法化的特性。结构等价在需要存储或通过网络传输类型化数据时具有独特的优势；相比之下，按名称等价在处理分时或分空间开发和编译的交互程序时较为困难。

在后续讨论中，我们假设使用结构等价。

The language of type systems

一个类型系统独立于具体的类型检查算法来指定编程语言的类型规则。这类似于通过形式化文法描述编程语言的语法，而和具体的解析算法相独立。

将类型系统与类型检查算法分离既方便又有用：类型系统属于语言定义的范畴，而算法则属于编译器的范畴。通过类型系统解释语言的类型特性比通过特定编译器使用的算法来解释更为容易。此外，不同的编译器可能会为同一个类型系统使用不同的类型检查算法。

从技术上讲，可以定义出只允许不可行的类型检查算法，甚至完全没有算法的类型系统。然而，通常来说类型系统的设计要允许有高效的类型检查算法。

Judgments

类型系统通常通过一种特定的形式化方法来描述。我们现在介绍这种形式化方法。描述一个类型系统的过程始于对一组称为判断（judgments）的形式化表达的定义。

一个典型的判断（Judgment）形式如下：

\[\Gamma \vdash \mathcal{J} \]

我们称 \(\Gamma\) 蕴含 \(\mathcal{J}\)。这里的 \(\Gamma\) 是一个静态类型环境；例如，它是一个有序的、包含不同变量及其类型的列表，形式为 \(\cdot, x_1 : A_1, \dots, x_n : A_n\)。空环境用 \(\cdot\) 表示，而 \(\Gamma\) 中声明的变量集合（即 \(x_1, \dots, x_n\)）被记为 \(\text{dom}(\Gamma)\)，即 \(\Gamma\) 的域（domain）。断言 \(\mathcal{J}\) 的形式在不同的判断中可能有所不同，但 \(\mathcal{J}\) 中的所有自由变量都必须在 \(\Gamma\) 中声明。

对于我们当前的目的，最重要的判断是类型判断（typing judgment）。它断言一个项 (M) 在其自由变量的静态类型环境下具有类型 (A)。类型判断的形式为：

\[\Gamma \vdash M : A \]

这里，\(\Gamma\) 是静态类型环境，描述了 \(M\) 的自由变量及其类型。

还需要再加入其他的判断形式；一个常见的形式是简单地断言一个环境是良构的（well-formed）：

\[\Gamma \vdash \Diamond \]

这表示环境 \(\Gamma\) 是良构的，即其中的所有变量及其类型声明都是有效的。任何给定的判断都可以被视为有效（例如，\(\Gamma \vdash \text{true} : \text{Bool}\)）或无效（例如，\(\Gamma \vdash \text{true} : \text{Nat}\)）。有效性形式化地定义了程序类型正确的概念。有效判断和无效判断之间的区分可以通过多种方式表达。然而，一种高度结构化的方式已经成为主流，用于描述有效判断的集合。这种表达方式基于类型规则，它在陈述和证明关于类型系统的技术引理和定理时非常有用。此外，类型规则具有高度的模块化：不同构造的规则可以单独书写（与单一的、整体化的类型检查算法形成对比）。因此，类型规则相对来说更易于阅读和理解。

Type rules

类型规则通过基于已知有效的其他判断来断言某些判断的有效性。这个过程通常从一些显然正确的判断开始。例如：

\[\emptyset \vdash \Diamond \]

这表明空环境是良构的。这种初始判断为整个类型系统的推导过程提供了基础。

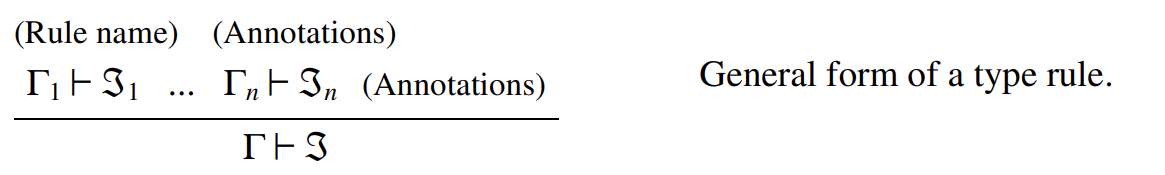
每条类型规则都以若干前提判断（\(\Gamma_i \vdash \mathcal{J}_i\)）书写在横线的上方，并在横线的下方给出一个单一的结论判断（\(\Gamma \vdash \mathcal{J}\)）。当所有前提都满足时，结论必须成立；前提的数量可以为零。每条规则都有一个名称。（根据惯例，规则名称的第一个单词由结论判断的类型决定。例如，名称形式为“(Val ...)”的规则，其结论通常是一个值类型判断。）在需要时，规则适用范围的限制条件，以及规则中使用的缩写，也会标注在规则名称旁边或前提的附近。

例如，以下两条规则中的第一条表明，在任何良构的环境 \(\Gamma\) 中，任何数字都是类型为 \(\text{Nat}\) 的表达式。第二条规则表明，两个表示自然数的表达式 \(M\) 和 \(N\) 可以组合成一个更大的表达式 \(M + N\)，该表达式同样表示一个自然数。此外，\(M\) 和 \(N\) 所在的环境 \(\Gamma\)（用于声明 \(M\) 和 \(N\) 中任意自由变量的类型）会延续到 \(M + N\)。

前面提到的基本规则表明，空环境在没有任何假设的情况下是良构的。

一组类型规则被称为一个（形式化的）类型系统。从技术上讲，类型系统属于形式化证明系统的通用框架：它是一组用于逐步推导的规则。在类型系统中，进行的推导与程序的类型判定相关。

Type derivations

在给定类型系统中的推导是一个由判断组成的树结构，树的叶子（可能是多个前提）位于顶部，根（一个结论）位于底部。每个判断通过类型系统中的某条规则从其直接上方的判断推导而来。类型系统的一个基本要求是，必须能够检查一个推导是否被正确构造出来。这意味着我们需要能够验证每一步推导是否符合类型规则，以及整个推导树是否遵循类型系统的结构和约束。这种检查确保了类型系统的可靠性和一致性，从而保证程序的类型判定是正确的。

一个有效判断是指可以通过在给定类型系统中正确构造推导树而获得的结论。换句话说，只有通过正确应用类型规则推导出的判断才是有效的。例如，假设我们之前展示了三个类型规则，可以用它们来构造以下推导树，证明 \(1 + 2 : \text{Nat}\) 是一个有效判断。推导树的每一步都显示了应用的规则，具体如下：

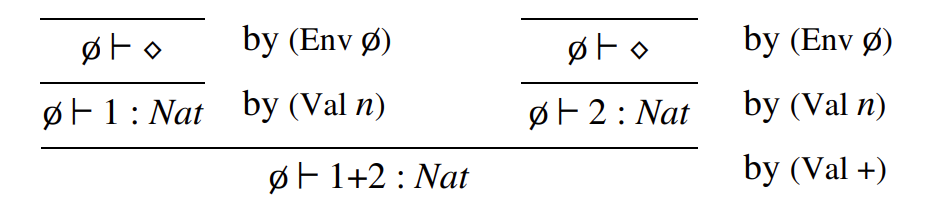
Well typing and type inference

在给定的类型系统中，如果存在某个类型 \(A\)，使得 \(\Gamma \vdash M : A\) 是一个有效判断，那么术语 \(M\) 在环境 \(\Gamma\) 下是良类型的；也就是说，如果项 \(M\) 能够被赋予某种类型，那么它就是良类型的。发现一个项的推导（进而发现其类型）的过程被称为类型推断问题。在由以下规则组成的简单类型系统中： \(Env\) 环境规则 \(Val n\) 自然数值规则 \(Val +\) 加法规则，可以在空环境下（\(\Gamma = \emptyset\)）为术语 \(1 + 2\) 推断出一个类型。根据之前的推导，这个类型是 \(\text{Nat}\)。

假设我们现在向类型系统中添加一个新的类型规则，其前提是 $\Gamma \vdash \Diamond $, 结论是 \(\Gamma \vdash \text{true} : \text{Bool}\)。在这个扩展后的类型系统中，我们无法为术语 \(1 + \text{true}\) 推断出任何类型，因为没有规则允许将一个自然数与一个布尔值相加。由于不存在任何推导可以支持 \(1 + \text{true}\)，我们称 \(1 + \text{true}\) 不可类型化，或者说它是类型不良的（ill-typed），又或者说它存在类型错误（typing error）。

我们还可以进一步添加一个类型规则，其前提是 \(\Gamma \vdash M : \text{Nat}\) 和 \(\Gamma \vdash N : \text{Bool}\)，结论是 \(\Gamma \vdash M + N : \text{Nat}\)（例如，意图将布尔值 \(\text{true}\) 解释为 \(1\)）。在这样的类型系统中，可以为术语 \(1 + \text{true}\) 推断出一个类型，这样它就会成为良类型的。

因此，给定项的类型推断问题取决于所讨论的类型系统。类型推断算法的难易程度完全取决于具体的类型系统。对于某些类型系统，找到类型推断算法可能非常容易，也可能极其困难，甚至根本无法找到。即使能够找到，最优算法可能非常高效，也可能慢得无法接受。类型系统通常以抽象的形式表达和设计，但它们的实用性却依赖于是否能够提供好的类型推断算法。

显式类型的过程式语言（例如 Pascal）的类型推断问题相对容易解决；我们将在第 8 节中讨论这一点。而对于隐式类型语言（例如 ML）的类型推断问题则要微妙得多，我们在这里不作讨论。尽管基本的算法已经被很好地理解（文献中有多种描述），并且被广泛使用，但实践中使用的算法版本较为复杂，目前仍在研究之中。

当涉及多态性时（在第 5 节中讨论），类型推断问题变得特别困难。对于 Ada、CLU 和 Standard ML 等语言中显式类型的多态特性，其类型推断问题在实践中是可处理的。然而，这些问题通常通过算法解决，而不先描述相关的类型系统。最纯粹且最通用的多态类型系统体现在第 5 节中讨论的 λ 演算中。对于这种多态 λ 演算的类型推断算法相对简单，我们将在第 8 节中介绍它。然而，解决方案的简单性依赖于不切实际的极为冗长的类型注解。为了使这种通用多态性在实践中可行，必须允许适当的省略某些类型信息。这类类型推断问题仍然是一个活跃的研究领域。

Type soundness

我们现在已经建立了关于类型系统的所有一般概念，可以开始研究具体的类型系统。从第 3 节开始，我们将回顾一些非常强大但相对理论化的类型系统。这样做的目的是，通过首先理解这些类型系统，编写针对编程语言中各种复杂特性的类型规则也会更容易。

当我们深入研究类型规则时，应牢记一个合理的类型系统不仅仅是任意规则的集合。良好的类型设计旨在对应于程序行为的语义概念。通常，通过证明类型健全性定理来检查类型系统的内部一致性。这正是类型系统与语义相结合的地方。对于指称语义（denotational semantics），我们期望如果 $ \Gamma \vdash M : A $ 成立，那么 $ [ M ] \in [ A ] $ 也成立（即 $ M $ 的值属于由类型 $ A $ 表示的值的集合）。对于操作语义（operational semantics），我们期望如果 $ \Gamma \vdash M : A $ 且 $ M $ 归约为 $ M' $，那么 $ \Gamma \vdash M' : A $ 也成立。在这两种情况下，类型健全性定理都断言：良类型的程序在计算时不会发生运行错误。

First-order Type Systems

大多数常见的过程式语言中的类型系统被称为一阶类型系统（first-order type systems）。在类型理论术语中，这意味着它们缺乏类型参数化（type parameterization）和类型抽象（type abstraction），而这些特性属于二阶特性（second-order features）。令人稍感困惑的是，一阶类型系统实际上可以包含高阶函数（higher-order functions）。例如，Pascal 和 Algol68 拥有相对丰富的一阶类型系统，而 FORTRAN 和 Algol60 的一阶类型系统则非常有限。

一个最小的一阶类型系统可以应用于无类型的λ-演算上，其中无类型的 λ-抽象 $ \lambda x.M $ 表示一个以参数 $ x $ 为输入、以 $ M $ 为结果的函数。为这个演算提供类型只需要函数类型和一些基本类型；稍后我们将看到如何添加其他常见的类型结构。

一阶类型化的 λ-演算被称为 \(\text{System F}_1\)。与无类型 λ-演算的主要区别是为 λ-抽象添加了类型注解，使用的语法是 $ \lambda x:A.M $，其中 $ x $ 是函数的参数，$ A $ 是其类型，$ M $ 是函数的主体。（在一个类型化的编程语言中，我们可能还会包括函数返回的结果的类型，但在这里并不必要。）从 $ \lambda x.M $ 到 $ \lambda x:A.M $ 的转变是从无类型语言到类型化语言的典型步骤：绑定变量会获得类型注解。

由于 \(F_1\) 主要基于函数值，最有趣的类型是函数类型：$ A \to B $ 表示具有参数类型为 $ A $ 且结果类型为 $ B $ 的函数的类型。不过，为了开始，我们还需要一些基本类型来构建函数类型。我们用 Basic 表示这样一组基本类型，并用 $ K \in \text{Basic} $ 表示任意一个这样的基本类型。目前，基本类型仅仅是技术上的必要性，但很快我们会考虑一些有趣的基本类型，比如 Bool 和 Nat。

\(F_1\) 的语法如表 2 所示。在类型化语言中，讨论语法的作用是非常重要的。在无类型 λ-演算中，无上下文语法（context-free syntax）精确地描述了合法的程序。然而在类型化演算中，情况并非如此，因为良好行为通常不是一个无上下文的性质。描述合法程序的任务由类型系统接管。例如，表达式 $ \lambda x:K.x(y) $ 符合表中 \(F_1\) 的语法规则，但它不是 \(F_1\) 的合法程序，因为它不是类型正确的，因为 $ K $ 不是一个函数类型。尽管如此，无上下文语法仍然是需要的，但其主要作用是定义自由变量和绑定变量的概念，也就是定义语言的作用域规则（scoping rules）。基于这些作用域规则，仅在绑定变量上不同的项，例如 $ \lambda x:K.x $ 和 $ \lambda y:K.y $，在语法上被认为是相同的。这种方便的等同关系在类型规则中被隐式假定（在应用某些类型规则时可能需要重命名绑定变量）。

note: 可以通过反证严格证明表达式不符合类型规则

我们只需要为 \(F_1\) 定义三个简单的判断规则，它们如表 3 所示。判断 $ \Gamma \vdash A $ 在某种意义上是有点多余的，因为所有语法上正确的类型 $ A $ 在任何环境 $ \Gamma $ 中都自然是良构的。然而，在二阶系统中，类型的良构性无法仅通过语法来捕获，因此判断 $ \Gamma \vdash A $ 变得至关重要。现在采用这个判断规则使得这样后续扩展会更加容易。

这些判断的有效性由表 4 中的规则定义。其中，规则 (Env \(\emptyset\)) 是唯一不需要任何前提假设的规则（即，它是唯一的公理）。它表明空环境是一个有效的环境。规则 (Env x) 用于将环境 $ \Gamma $ 扩展为更长的环境 $ \Gamma, x:A $，前提是 $ A $ 是 $ \Gamma $ 中的一个有效类型。需要注意的是，假设 $ \Gamma \vdash A $ 的过程会隐含着 $ \Gamma $ 是有效的环境，而且这一过程是递归的。换句话说，在推导 $ \Gamma \vdash A $ 的过程中，我们必须已经推导出 $ \Gamma \vdash \Diamond $。规则 (Env x) 的另一个要求是变量 $ x $ 不能已经在 $ \Gamma $ 中定义。我们特别注意保持环境中的变量互不相同，因此当 $ \Gamma, x:A \vdash M : B $ 被推导出来时（例如在规则 (Val Fun) 的假设中），我们可以确定 $ x $ 不会出现在 $ \text{dom}(\Gamma) $ 中（即 $ x $ 不属于 $ \Gamma $ 的域）。这种约束确保了环境的变量是唯一的，从而避免了变量冲突的问题。

规则 (Type Const) 和 (Type Arrow) 用于构造类型。规则 (Val x) 从环境中提取假设：我们使用符号 $ \Gamma', x:A, \Gamma'' $（相对非正式地）表示 $ x:A $ 在环境中的某处出现。规则 (Val Fun) 为函数赋予类型 $ A \to B $，前提是函数体在假设形式参数具有类型 $ A $ 的情况下被赋予类型 $ B $。请注意，在此规则中，环境的大小发生了变化，因为我们向环境中添加了新的变量 $ x $ 和它的类型 $ A $。规则 (Val Appl) 用于将函数应用于一个参数：在检验前提是否成立时，相同的类型 $ A $ 必须出现两次。这意味着函数的参数类型与实际传递给函数的参数类型必须一致，从而确保类型安全性。这些规则共同定义了 \(F_1\) 类型系统中的基本行为，包括如何构造类型、如何从环境中提取假设，以及如何验证函数的类型和应用的类型。

表 5 展示了一个相当长的但是使用了所有规则的推导：

现在我们已经研究了一个简单一阶类型系统的基本结构，可以开始对其进行扩展，使其更接近实际编程语言中的类型结构。我们将为每种新的类型构造添加一组规则，并遵循一种相当规律的模式。我们从一些基本数据类型开始：类型 \(Unit\)，它只有一个值，即常量 \(unit\)；类型 \(Bool\)，它的值是 \(true\) 和 \(false\)；以及类型 \(Nat\)，它的值是自然数。

类型 \(Unit\) 通常用于作为无关紧要的参数和结果的占位符；在某些语言中，它被称为 \(Void\) 或 \(Null\)。由于 \(Unit\) 类型上没有任何操作，因此我们只需要一个规则声明 \(Unit\) 是一个合法的类型，以及一个规则声明 \(unit\) 是 \(Unit\) 类型的合法值（见表 6）。

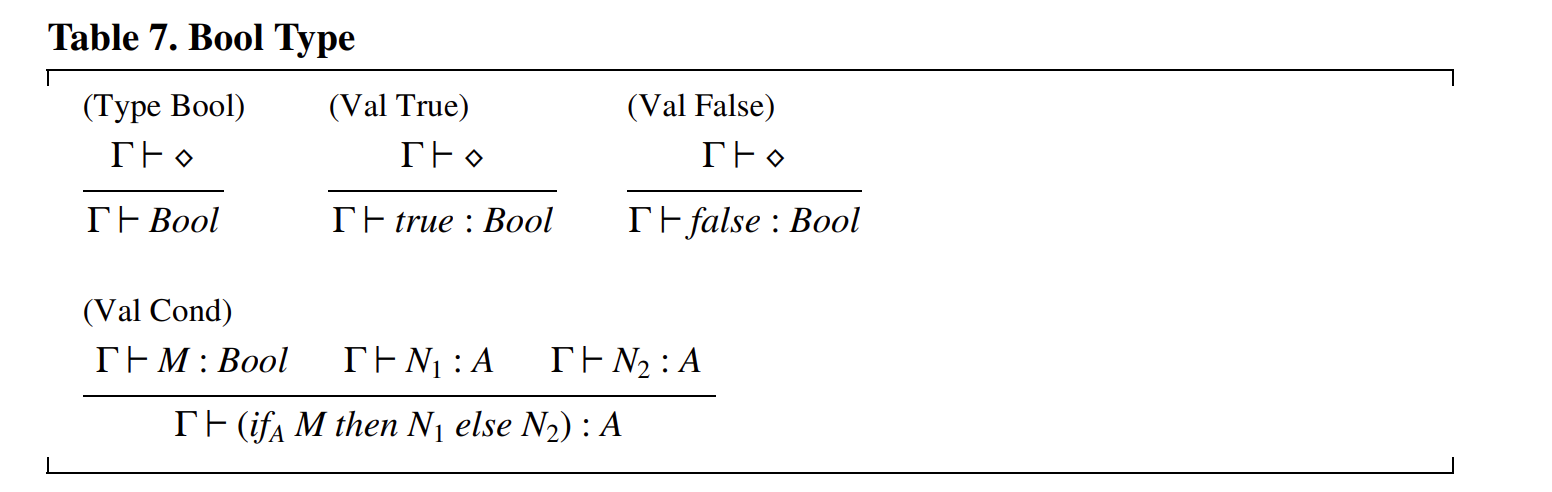
我们对 \(Bool\) 类型的规则遵循类似的模式，但布尔类型还具有一个有用的操作——条件表达式，它有自己的类型规则（见表 7）。在规则 (Val Cond) 中，条件表达式的两个分支必须具有相同的类型 \(A\)，因为任一分支都可能生成结果。

规则 (Val Cond) 展示了一个关于类型检查所需类型信息的微妙问题。当遇到条件表达式时，类型检查器必须分别推导出 \(N_1\) 和 \(N_2\) 的类型，然后找到一个与两者兼容的单一类型 \(A\)。在某些类型系统中，从 \(N_1\) 和 \(N_2\) 的类型中确定这个单一类型 \(A\) 可能并不容易，甚至可能无法实现。为了应对这种潜在的类型检查困难，我们使用“下标类型”来表达额外的类型信息：\(if_A\) 是对类型检查器的提示，表明结果类型应该是 \(A\)，并且推导出的 \(N_1\) 和 \(N_2\) 的类型应分别与给定的 \(A\) 进行比较。通常，我们使用带下标的类型来指示在特定类型系统中可能有用或必要的信息。类型检查器的任务通常是综合这些额外的信息。当可以综合这些信息时，下标可以被省略。（大多数常见的语言不需要这样的 \(if_A\) 注解。）

自然数类型 \(Nat\)（见表 8）以 \(0\) 和 \(succ\)（后继）作为生成器。或者，如我们之前所做的，可以用一条规则来声明所有数值常量都属于类型 Nat。 对 \(Nat\) 类型的计算由 \(pred\)（前驱）和 \(isZero\)（测试是否为零）这两个基本操作实现；当然，也可以选择其他集合的基本操作。

现在我们已经有了一些基本类型，可以开始研究结构化类型，从笛卡尔积类型开始（见表 9）。一个笛卡尔积类型 \(A_1 \times A_2\) 表示一对值的类型，其中第一个分量的类型是 \(A_1\)，第二个分量的类型是 \(A_2\)。这些分量可以分别通过投影操作 \(first\) 和 \(second\) 提取出来。除了（或作为补充）使用投影操作，还可以使用 \(with\) 语句来分解一个对 \(M\)，并将其分量分别绑定到两个独立的变量 \(x_1\) 和 \(x_2\)，供作用域 \(N\) 使用。\(with\) 这种记法与 ML 语言中的模式匹配有关，同时也与 Pascal 语言中的 \(with\) 语句存在联系；当我们进一步讨论记录类型时，与 Pascal 的联系会更加清晰。

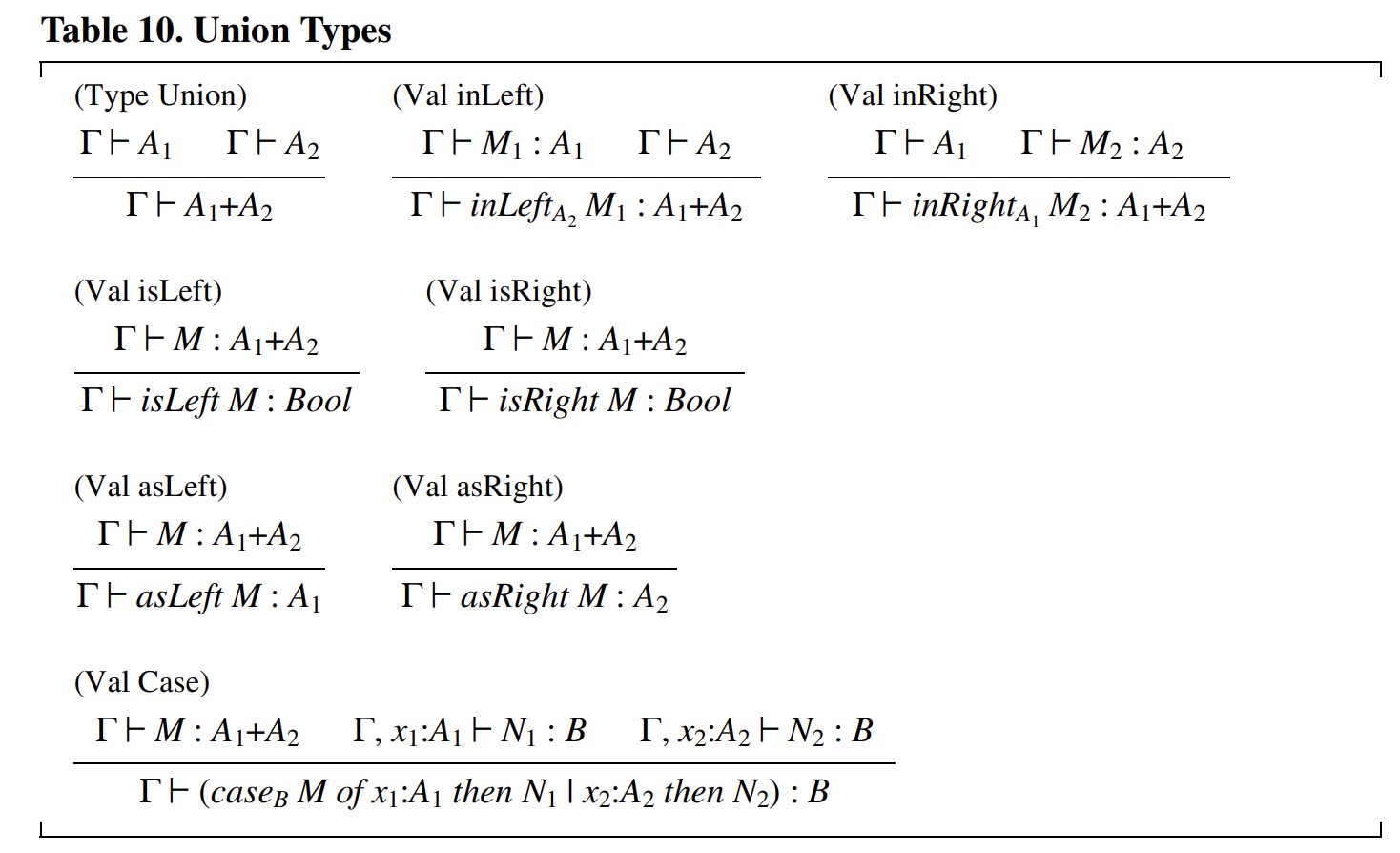
联合类型（Union types，见表 10）常常被忽视，但它们在表达能力上与笛卡尔积类型同样重要。联合类型 \(A_1 + A_2\) 的元素可以被看作是一个带有左标签（由 \(inLeft\) 创建）的 \(A_1\) 类型的元素，或者是一个带有右标签（由 \(inRight\) 创建）的 \(A_2\) 类型的元素。这些标签可以通过 \(isLeft\) 和 \(isRight\) 进行测试，并且可以通过 \(asLeft\) 和 \(asRight\) 提取对应的值。如果错误地将 \(asLeft\) 应用于一个带右标签的值，会产生一个捕获的错误或异常；这种捕获的错误不被视为禁止的错误。需要注意的是，假设 \(asLeft\) 的任何结果都属于类型 \(A_1\) 是安全的，因为参数要么是带左标签的，在这种情况下结果确实是 \(A_1\) 类型；要么是带右标签的，在这种情况下没有结果。与条件表达式的情况类似，下标被用来消除某些规则中的歧义。

规则 (Val Case) 描述了一种优雅的结构，它可以取代 \(isLeft\)、\(isRight\)、\(asLeft\)、\(asRight\) 以及相关的捕获错误。（同时，它也消除了联合操作对布尔类型 \(Bool\) 的任何依赖。）这个 \(case\) 结构根据 \(M\) 的标签执行两个分支之一，并将 \(M\) 的去标签内容分别绑定到 \(x_1\) 或 \(x_2\)，供 \(N_1\) 或 \(N_2\) 的作用域使用。分支之间用竖线 \(|\) 分隔。这种构造不仅更简洁，还避免了显式测试和提取标签的冗余操作，同时通过绑定去标签的内容直接进入逻辑分支，从而提高了代码的可读性和安全性。

从表达能力的角度来看（尽管不一定是实现的角度），可以注意到类型 \(Bool\) 可以被定义为 \(Unit + Unit\)，在这种情况下，\(case\) 结构可以简化为条件表达式。类似地，类型 \(Int\) 可以被定义为 \(Nat + Nat\)，其中一个 \(Nat\) 表示非负整数，另一个 \(Nat\) 表示负整数。我们还可以定义一个原型的捕获错误，如 $ \text{error}_A = \text{asRight}(\text{inLeft}_A(\text{unit})) : A $。因此，我们可以为每种类型构造一个错误表达式。

笛卡尔积类型和联合类型可以通过迭代扩展来生成元组类型和多重联合类型。然而，这些派生类型相对不够方便，因此在编程语言中很少见到。相反，通常使用带标签的积类型和联合类型：它们分别被称为记录类型和变体类型。

记录类型是一种熟悉的类型结构，它是带有名称的类型集合，其值级别的操作允许通过名称提取组件。表 11 中的规则假设记录类型和记录在语法上是等价的，允许对其带标签的组件进行重新排序；这种等价性类似于对函数的语法等价性，即允许对绑定变量进行重命名。

笛卡尔积类型的 \(with\) 语句被推广至记录类型，在规则 \((Val \ Record \ With)\) 中体现。记录 \(M\) 中带标签的组件 \(l_1, \dots, l_n\) 被绑定到变量 \(x_1, \dots, x_n\)，这些绑定变量的作用域为 \(N\)。Pascal 语言中也有类似的结构，也被称为 \(with\)，但其绑定变量是隐式的。这种设计有一个相当不幸的后果：作用域依赖于类型检查，从而导致难以追踪的错误，例如隐藏变量冲突。

笛卡尔积类型 \(A_1 \times A_2\) 可以被定义为 \(\text{Record}( \text{first}:A_1, \text{second}:A_2)\)。

变体类型（表 12）是带名称的独立类型的联合；它们在语法上可以通过重新排列组成部分来识别。构造 \(is\ l\) 是 \(isLeft\) 和 \(isRight\) 的推广，而构造 \(as\ l\) 是 \(asLeft\) 和 \(asRight\) 的推广。与联合类型类似，这些构造可以被替换为一个 \(case\) 语句，而该语句现在具有多个分支。

联合类型 \(A_1 + A_2\) 可以定义为 \(\text{Variant}(\text{left}:A_1, \text{right}:A_2)\)。枚举类型，例如 \(\{\text{red}, \text{green}, \text{blue}\}\)，可以定义为 \(\text{Variant}(\text{red}:\text{Unit}, \text{green}:\text{Unit}, \text{blue}:\text{Unit})\)。

引用类型（表 13）可以用作命令式语言中可变存储位置的基础类型。类型为 \(\text{Ref}(A)\) 的元素是一个可变单元，包含类型为 \(A\) 的元素。新的单元可以通过规则 \((\text{Val Ref})\) 分配，通过规则 \((\text{Val Assign})\) 更新，并通过规则 \((\text{Val Deref})\) 显式解引用。由于赋值操作的主要目的是执行副作用，其结果值被选择为 \(\text{Unit}\) 类型。

更有趣的是，数组及其操作可以如表 14 所示进行建模，其中 (\text{Array}(A)) 是一种数组类型，表示长度固定且元素类型为 (A) 的数组。表 14 中的代码当然是对数组的一种低效实现，但它说明了一个关键点：复杂的类型规则可以从更简单的类型规则中推导出来。表 15 中展示的数组操作的类型规则可以根据表 14 中的实现，结合笛卡尔积、函数和引用类型的规则，轻松推导出来。

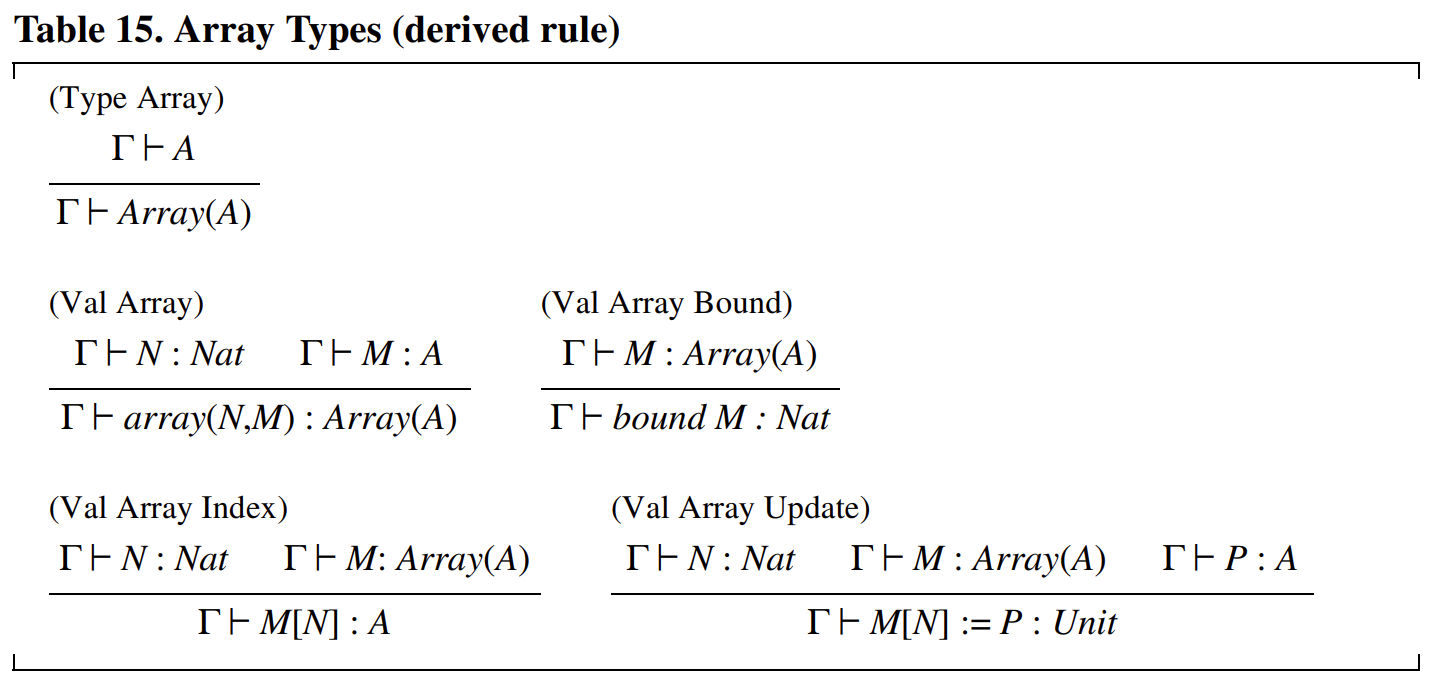
note: 其实还挺好理解的，一个有界数组是长度和映射组成的一个元组，当然还有别的构造方案

在大多数编程语言中，类型可以递归定义。递归类型非常重要，因为它们使其他类型构造更加有用。递归类型通常是隐式引入的，或者缺乏精确的解释，并且它们的特性相当微妙。因此，对递归类型进行形式化定义需要特别谨慎。

对递归类型的处理需要对 \(F_1\) 进行一个相当基础的扩展：需要将环境扩展为包含类型变量 \(X\)。这些类型变量用于形如 \(\mu X.A\) 的递归类型（见表 16），其直观上表示递归方程 \(X = A\) 的解，其中 \(X\) 可以出现在 \(A\) 中。操作 \(\text{unfold}\) 和 \(\text{fold}\) 是显式的类型转换，它们在递归类型 \(\mu X.A\) 和其展开形式 \([\mu X.A / X]A\)（其中 \([B / X]A\) 表示将 \(A\) 中所有自由出现的 \(X\) 替换为 \(B\)）之间进行映射，反之亦然。这些类型转换在运行时没有任何实际效果（即满足 \(\text{unfold}(\text{fold}(M)) = M\) 和 \(\text{fold}(\text{unfold}(M')) = M'\)）。在实际的编程语言语法中，这些操作通常被省略，但它们的存在使得递归类型的形式化处理更加容易。

note: 不太记得miu算子是什么了，等会复习下

递归类型的一个标准应用是结合乘积类型和并集类型来定义列表和树的类型。元素类型为 \(A\) 的列表类型 \(\text{List}_A\) 定义如下（见表 17），同时包括列表构造器 \(\text{nil}\) 和 \(\text{cons}\)，以及列表分析器 \(\text{listCase}\)。

递归类型可以与记录类型（record types）和变体类型（variant types）结合使用，用于定义复杂的树结构，例如抽象语法树（abstract syntax trees, AST）。通过使用 \(\text{case}\) 和 \(\text{with}\) 语句，可以方便地分析这些树结构。

当递归类型与函数类型结合使用时，其表达能力令人惊讶。通过巧妙的编码，可以证明在值层级的递归实际上已经隐含在递归类型中：无需将递归作为一个单独的构造来引入。此外，在递归类型的存在下，可以在类型化语言中实现无类型编程。更具体地说，表 18 展示了如何为任意类型 \(A\) 定义一个发散元素 \(\bot_A\) 以及该类型的一个不动点算子\(\text{fix}_A\)。表 19 展示了如何在类型化计算中对无类型 \(\lambda\)-演算进行编码。（这些编码适用于按需调用；在按值调用中，它们的形式略有不同。）

在递归类型的背景下，类型等价变得尤为有趣。我们通过以下方式规避了一些问题：不处理类型定义，要求在递归类型与其展开形式之间显式使用折叠和展开的强制转换，并且不假设递归类型之间的任何等价关系，除了对绑定变量的重命名。在当前的形式化中，我们无需定义一个正式的类型等价判断：两个递归类型仅在结构上完全相同（允许绑定变量的重命名）时才视为等价。这种简化的方法可以扩展，以包括类型定义和基于递归类型展开的类型等价关系。

First-order Type Systems for Imperative Languages

Second-order Type Systems

Subtyping