2021ACM集训队个人赛4C题

原题链接：xinz

描述

给你一个字符串，比如：yacrrqeou，你发现其由三个单词组成：are、you和crq，每个单词的字母顺序与原字符串保持一致，且每个字母只能用一次，而三个单词的总长度与原字符串相同。

现在已知三个单词是从某个字符串s分拆出来的，求总共有多少种分拆方法？

输入

输入共四行，前三行为三个单词，每个单词长度在1~100之间。

第四行为字符串s，总长度等于三个单词长度之和。

输出

求分拆方法数，由于结果可能很大，只需要对1000000007取余。

样例输入

are
you
crq
yacrrqeou

样例输出

2

题解

• 这题我是用状态机来思考的
• 一共可以分为三个状态，分别是第i个字符应该放在哪个字符串中
  
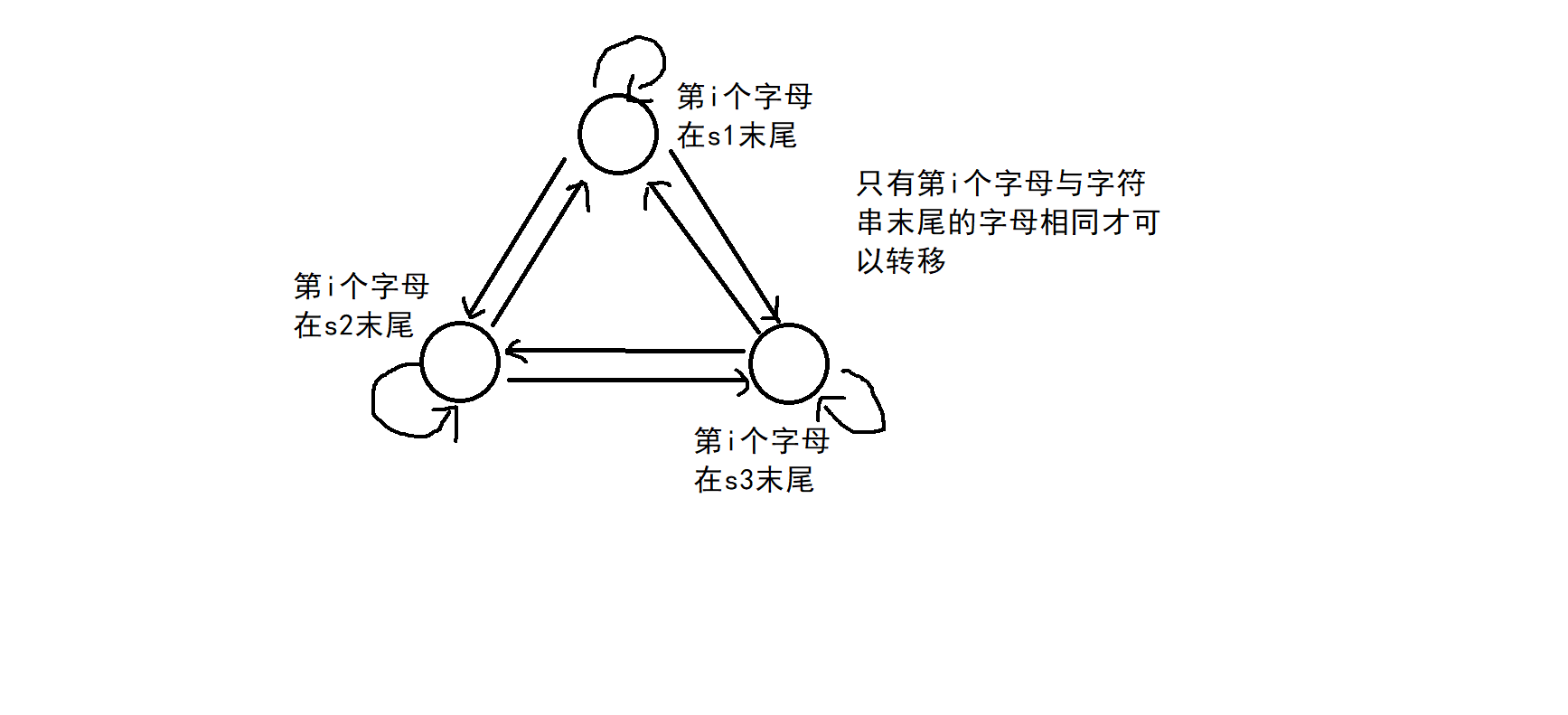
• 因此对于每个状态f(j,k,l)从三个状态转移过来，分别是f(j-1,k,l),f(j,k-1,l),f(j,k,l-1)。在放入第i个字母前要保证前i个字母都已经放入三个字符串中，所以需要满足i=j+k+l。
  

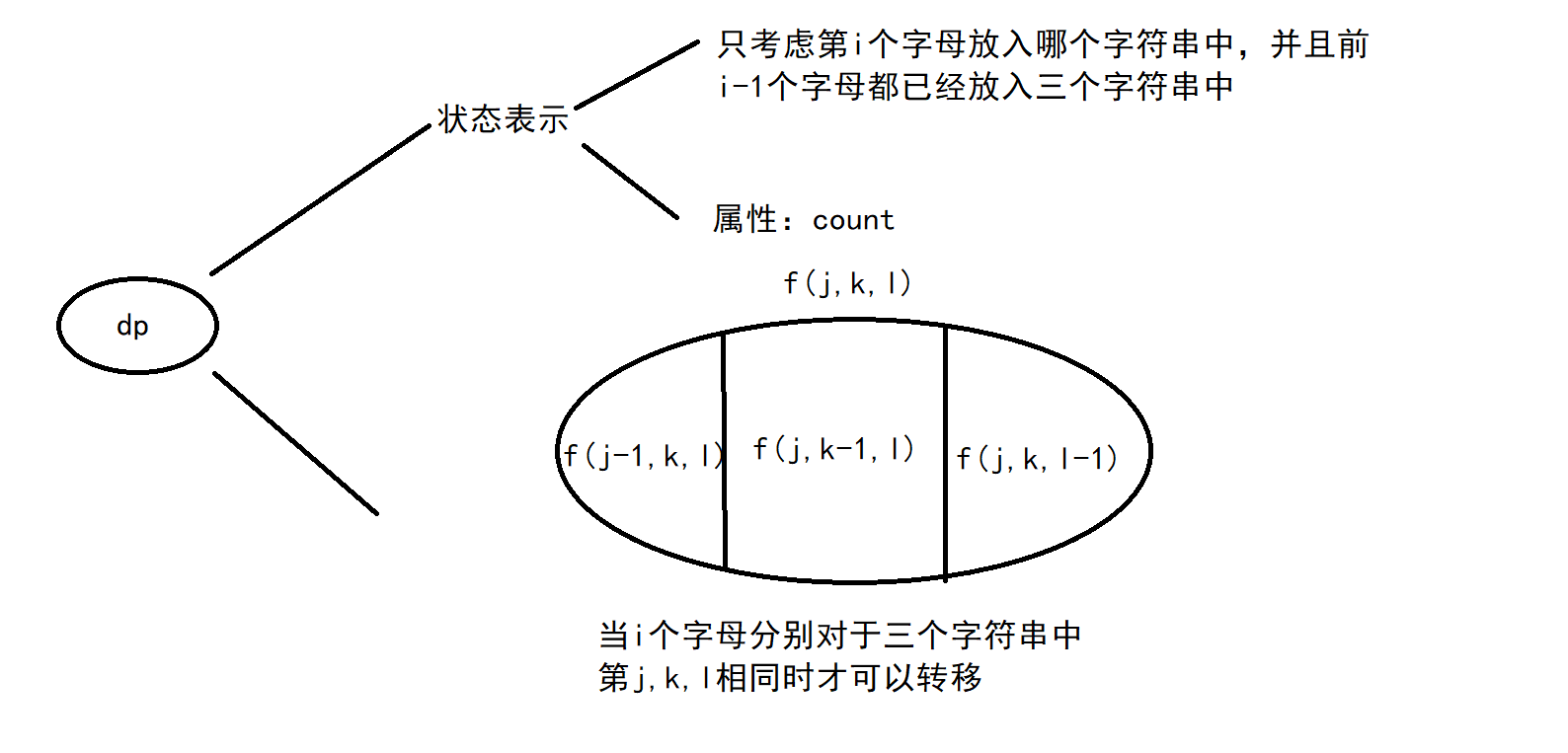
AC代码

#include<iostream>
#include<string>
#include<cstring>
using namespace std;
const int mod=1000000007;
typedef long long ll;
int sum[2][102][102][102];//不用滚动数组应该是sum[305][102][102][102]
char s1[102],s2[102],s3[102];
char s[305];
int main(){
    int n1,n2,n3,n,flag=0;
    scanf("%s%s%s%s",s1+1,s2+1,s3+1,s+1);
    n1=strlen(s1+1);
    n2=strlen(s2+1);
    n3=strlen(s3+1);
    n=strlen(s+1);
    sum[0][0][0][0]=sum[1][0][0][0]=1;
    for(int i=1;i<=n;i++){
        for(int j=0;j<=n1&&j<=i;j++){
            for(int k=0;k<=n2&&k<=i-j;k++){
                int l=i-j-k;
                sum[flag][j][k][l]=sum[!flag][j][k][l];
                if(s[i]==s1[j])sum[flag][j][k][l]=((ll)sum[flag][j][k][l]+sum[!flag][j-1][k][l])%mod;
                if(s[i]==s2[k])sum[flag][j][k][l]=((ll)sum[flag][j][k][l]+sum[!flag][j][k-1][l])%mod;
                if(s[i]==s3[l])sum[flag][j][k][l]=((ll)sum[flag][j][k][l]+sum[!flag][j][k][l-1])%mod;
            }
        }
        flag=!flag;
    }
    printf("%d",sum[!flag][n1][n2][n3]);
    return 0;
}