AtCoder ABC 365题解
前言
本文集结网络上的题解,方便查阅。
A - Leap Year
题目大意
判断闰年
解题思路
根据题目模拟即可。
code
#include <bits/stdc++.h>
using namespace std;
int main() {
int n;
scanf("%d", &n);
if(n % 4 != 0) {
printf("365\n");
} else if(n % 4 == 0 && n % 100 != 0) {
printf("366\n");
} else if(n % 100 == 0 && n % 400 != 0) {
printf("365\n");
} else if(n % 400 == 0) {
printf("366\n");
}
return 0;
}
B - Second Best
题目大意
输出第二大的数的下标。
解题思路
对下标排序,输出第二个即可。
code
#include <bits/stdc++.h>
using namespace std;
int a[105];
int ind[105];
bool cmp(int i, int j) {
return a[i] > a[j];
}
int main() {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", a + i);
ind[i] = i;
}
sort(ind + 1, ind + 1 + n, cmp);
printf("%d\n", ind[2]);
return 0;
}
C - Transportation Expenses
题目大意
给定n个人的交通费,求出最大的交通补贴额 \(x\) ,使得总交通补贴额 \(\sum \min(x,a_i)\) 不超过 \(m\) 。
解题思路
显然,如果 \(\sum a_i \leq m\) ,则无论 \(x\) 多大,总交通补贴额永远不会超过 \(m\) 。此时应当输出 infinite 。
否则,二分查找 \(x\) ,每一次计算补贴额度就直接 \(for\) 循环。求出 \(\sum \max(x,a_i)\) 即可。
code
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
int a[200005];
ll check(int x, int n) {
ll sum = 0;
for (int i = 1; i <= n; i++) {
sum += min(a[i], x);
}
return sum;
}
int search(int l, int r, int n, ll m) {
int mid;
while (l < r) {
mid = (l + r + 1) / 2;
if (check(mid, n) > m) r = mid - 1;
else l = mid;
}
return l;
}
int main() {
int n, maxx;
ll m, cnt = 0;
scanf("%d%lld", &n, &m);
for (int i = 1; i <= n; i++) {
scanf("%d", a + i);
cnt += a[i];
maxx = max(maxx, a[i]);
}
if (cnt <= m) {
printf("infinite\n");
return 0;
}
printf("%d\n", search(1, maxx, n, m));
return 0;
}
D - AtCoder Janken 3
题目大意
\(Takahashi\) 和 \(Aoki\) 玩石头剪刀布,给定 \(Aoki\) 出的手势,当
- \(Takahashi\) 从来没有输过。
- \(Takahashi\) 没有出过两个连续的手势。
时,\(Takahashi\) 最多能赢多少局?
解题思路
考虑 \(Takahashi\) 能出的手势只与 \(Aoki\) 这一局出的手势和 \(Takahashi\) 上一局出的手势有关,所以设 \(dp[i][j]\) 表示前 \(i\) 局,\(Takahashi\) 在第 \(i\) 局出了 \(j\) 的最大获胜数,每一个 \(dp[i][j]\) 从 \(dp[i - 1][*]\) 转移过来即可。
同时,需要注意,如果 \(j\) 手势会使 \(Takahashi\) 输掉第 \(i\) 局比赛,则 \(dp[i][j]\) 等于极小值,
code
#include <bits/stdc++.h>
using namespace std;
int dp[3], dp2[3];
int main() {
int n;
string s;
cin >> n >> s;
map<char, int> tie{{'R', 0}, {'P', 1}, {'S', 2}};
map<int, int> win{{0, 1}, {1, 2}, {2, 0}};
for (int i = 0; i < n; i++) {
dp2[0] = -0x3f3f3f3f;
dp2[1] = -0x3f3f3f3f;
dp2[2] = -0x3f3f3f3f;
int pid = tie[s[i]];
int id = win[pid];
for (int j = 0; j < 3; j++) {
if (j != id) {
dp2[id] = max(dp2[id], dp[j] + 1);
}
if (j != pid) {
dp2[pid] = max(dp2[pid], dp[j]);
}
}
dp[0] = dp2[0];
dp[1] = dp2[1];
dp[2] = dp2[2];
}
printf("%d\n", max(dp[0], max(dp[1], dp[2])));
return 0;
}
E - Xor Sigma Problem
题目大意
给定 \(A_1,\ A_2,\ ...,\ A_N\) ,求
解题思路
考虑每一个二进制位对结果的贡献。
考虑如何求 \(cnt\) 。
对于二进制第 \(k\) 位,用 \(odd_i\) 表示 \(A_i\) 的二进制位的第 $k $ 位是不是 \(1\) 。然后考虑有多少个区间异或和为 \(1\) 。
区间异或和和区间和一样,也可以使用前缀和优化。令 \(sum_i = A_1 \oplus A_2 \oplus ... \oplus A_i\) ,则 \(A_i \oplus A_{i + 1} \oplus ... \oplus A_j = sum_j \oplus sum_{i - 1}\) 。
因为我们要求有多少对 \((i,j)\) 满足 \(sum_j \oplus sum_{i - 1} = 1\) ,所以我们可以枚举 \(j\) ,再枚举 对应的 \(i\) 的数量。
因为:
- 如果 \(sum_j = 1\) ,则 \(sum_{i - 1} = 0\) 。
- 如果 \(sum_j = 0\) ,则 \(sum_{i - 1} = 1\) 。
所以,我们在枚举 \(j\) 时,实时维护 \(sum_i = 1\) 和 \(sum_i = 0\) 的数量然后根据 \(odd_j\) 的值,就可以知道 \(i\) 的值。
得到所有符合条件的 \((i,j)\) 的数量即 \(cnt_k\) 后,计算出每一位所做的贡献 \(2^icnt\) ,每一位所作贡献之和即为答案。
注意,上面的方案包含 \(i = j\) 情况,然而题目要求 \(i < j\) ,所以最后还需要减去一个 \(\sum_{i = 1}^n A_i\) 。
code
#include <bits/stdc++.h>
#define MAX_N 200005
using namespace std;
using LL = long long;
int a[MAX_N];
LL solve(int k, int n) {
vector<int> odd(n + 1, 0);
for (int i = 1; i <= n; i++) {
odd[i] = (a[i] >> k) & 1;
}
for (int i = 2; i <= n; i++) {
odd[i] ^= odd[i - 1];
}
LL ans = 0;
int m[2] = {1, 0};
for (int i = 1; i <= n; i++) {
ans += m[odd[i] ^ 1];
m[odd[i]]++;
}
return ans;
}
int main() {
int n;
scanf("%d", &n);
for (int i = 1; i <= n; i++) {
scanf("%d", a + i);
}
LL ans = 0;
for (int i = 0; i <= 31; i++) {
ans += (1LL << i) * solve(i, n);
}
for (int i = 1; i <= n; i++) {
ans -= a[i];
}
printf("%lld\n", ans);
return 0;
}
F - Takahashi on Grid
题目大意
\(Takahashi\) 站在一个网格上,求从 \((sx,sy)\) 走到 \((tx,ty)\) 的最短距离。
注意,\((i,j)\) 表示第 \(i\) 列,第 \(j\) 行。
解题思路
实际上,\(Takahashi\) 的行走方案分为上下移动和左右移动,我们可以重复执行这两步直到走到第 \(tx\) 列。
- 第一步:让 \(Takahashi\) 先一直向右移动,直到碰到墙,也就是移动到 \(y < l[x + 1]\) 或 \(y > r[x + 1]\) 。
- 第二步:再上下移动到 \(l[x + 1] \leq y \leq r[x + 1]\) 。
为了快速的找到每一次 \(Takahashi\) 碰到哪一列的墙,我们维护两个ST表 \(L\) 和 \(R\) ,每次二分查找一个 \(nxt\) ,使得 \(nxt\) 是第一个使得 \(L.query(x,nxt) > y\) 或 \(R.query(x,nxt) < y\) 的数。这个方法的时间复杂度仅有 \(\textrm{O}(\log n)\)。
为了能够快速知道执行完第一部和第二步后 \(Takahashi\) 在哪里,我们预处理一个倍增数组 \(run[i][x][0/1]\) ,即 \(Takahashi\) 从第 \(x\) 列的上/下端点开始走了 \(2^i\) 次第一步和第二步后,会走到哪一列的上/下端点,用了多少步。
对于每一次询问,我们先执行一次第一步和第二步使得 \(Takahashi\) 站在某一列的上/下端点,统计这些操作用了多少步。之后,通过倍增数组 \(run\) 来计算 \(Takahashi\) 走到 \((tx,ty)\) 需要用多少步。注意,这里用倍增数组可能不能直接到达 \((tx,ty)\) ,所以需要在执行一次第一步,最后上下移动到 \((tx,ty)\) 。
code
#include <bits/stdc++.h>
using namespace std;
using LL = long long;
using VT = vector<int>;
using VVT = vector<VT>;
using A = array<LL, 3>;
using VA = vector<A>;
using VVA = vector<VA>;
using VVVA = vector<VVA>;
class SparseTable {
private:
using F = function<int(const int &, const int &)>;
int n;
VVT m;
F fun;
public:
void init(const VT &a, F f) {
fun = f;
n = a.size();
int maxLog = 32 - __builtin_clz(n);
m.resize(n + 1, VT(maxLog + 1));
for (int i = 1; i < n; i++) {
m[i][0] = a[i];
}
for (int j = 1; j <= maxLog; j++) {
for (int i = 1; i <= n - (1 << (j - 1)); i++) {
m[i][j] = fun(m[i][j - 1],
m[i + (1 << (j - 1))][j - 1]);
}
}
}
int query(int from, int to) {
int lg = 32 - __builtin_clz(to - from + 1) - 1;
return fun(m[from][lg], m[to - (1 << lg) + 1][lg]);
}
};
VVVA run;
SparseTable L;
SparseTable R;
VT l;
VT r;
int n;
void jiebao(const A &arr, LL &a, LL &b, LL &c) {
a = arr[0];
b = arr[1];
c = arr[2];
}
int step(int x, int y) {
int l = x, r = n + 1;
while (l < r) {
int mid = (l + r) / 2;
if (L.query(l, mid) <= y && R.query(l, mid) >= y) {
l = mid + 1;
} else {
r = mid;
}
}
return l;
}
LL solve(int sx, int sy, int tx, int ty) {
if (sx == tx) {
return abs(sy - ty);
}
if (sx > tx) {
swap(sx, tx);
swap(sy, ty);
}
int nxt = step(sx, sy);
if (nxt > tx) {
return tx - sx + abs(sy - ty);
}
int d = (sy < l[nxt] ? 0 : 1);
LL nnxt, dd, ccost;
LL ret = nxt - sx + (d ? sy - r[nxt] : l[nxt] - sy);
sx = nxt;
for (int i = 31; i >= 0; i--) {
jiebao(run[i][sx][d], nnxt, dd, ccost);
if (nnxt <= tx) {
ret += ccost;
sx = nnxt;
d = dd;
}
}
ret +=
tx - sx + (d ? abs(ty - r[sx]) : abs(l[sx] - ty));
return ret;
}
int main() {
scanf("%d", &n);
l.resize(n + 5);
r.resize(n + 5);
for (int i = 1; i <= n; i++) {
scanf("%d%d", &l[i], &r[i]);
}
l[n + 1] = 0x3f3f3f3f;
r[n + 1] = -0x3f3f3f3f;
run.resize(40, VVA(n + 1, VA(2, A())));
L.init(l, [](int i, int j) { return max(i, j); });
R.init(r, [](int i, int j) { return min(i, j); });
LL nxt, d, cost, nnxt, dd, ccost;
for (int i = 1; i <= n; i++) {
for (int j = 0; j < 2; j++) {
int x = i, y = (j ? r[i] : l[i]);
nxt = step(x, y);
if (nxt == n + 1) {
run[0][i][j] = {n + 1, 0, n - i + 1};
} else if (y < l[nxt]) {
run[0][i][j] = {
nxt, 0, nxt - i + l[nxt] - y};
} else {
run[0][i][j] = {
nxt, 1, nxt - i + y - r[nxt]};
}
}
}
for (int i = 1; i <= 32; i++) {
for (int j = 1; j <= n; j++) {
for (int k = 0; k < 2; k++) {
jiebao(run[i - 1][j][k], nxt, d, cost);
if (nxt == n + 1) {
run[i][j][k] = {n + 1, 0, cost};
} else {
jiebao(run[i - 1][nxt][d],
nnxt,
dd,
ccost);
run[i][j][k] = {nnxt, dd, cost + ccost};
}
}
}
}
int q, sx, sy, tx, ty;
scanf("%d", &q);
while (q--) {
scanf("%d%d%d%d", &sx, &sy, &tx, &ty);
printf("%lld\n", solve(sx, sy, tx, ty));
}
return 0;
}
G - AtCoder Office
题目大意
有 \(n\) 个人在办公室外面,给你 \(m\) 条退出勤记录,求 \(L\) 和 \(U\) 共同处在办公室的总时间。
解题思路
根号分治。
定义一个阈值 \(\theta \approx \sqrt{m}\) ,所有记录条数不小于 \(\theta\) 的人为 \(a\) 类人,记录条数小于 \(\theta\) 的人为 \(b\) 类人。
首先预处理出所有 \(a\) 类人和其他人的答案。如果询问的两个人中有一个人是 \(a\) 类人,则直接输出答案,否则暴力求出答案。
为了求出每一个 \(a\) 类人和其他人对应的答案,我们定义一个数组 $tmp[i] $ ,表示第 \(i\) 条记录的时间。注意,此时间非彼时间,可以理解为当这一个 \(a\) 类人进入办公室时,时间开始流逝,当这个 \(a\) 类人出办公室时,时间暂停。
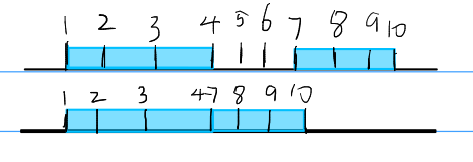
图中上面的时间轴是正常的时间,下面的时间轴是处理过后的 \(tmp\) 数组对应的时间。这样就可以利用 \(tmp\) 数组快速求出 \(a\) 类人和其他人在一个时间区间内共处在办公室的总时间。
由于最多有 \(\cfrac{m}{\theta} \approx \sqrt{m}\) 个 \(a\) 类人,所以预处理所有 \(a\) 类人和其他人的答案需要的时间为 \(\textrm{O}((n + m)\sqrt{m})\)。而暴力求解的时间复杂度为 \(\textrm{O}(\sqrt{m})\)。所以最终的时间复杂度为 \(\textrm{O}((n + m + q )\sqrt{m})\) ,其中 \(q\) 为询问次数。
code
#include <bits/stdc++.h>
#define MAX_N 200005
using namespace std;
int n, m, q, tot;
int T[MAX_N], P[MAX_N];
int ma[MAX_N], ans[1000][MAX_N];
vector<int> t[MAX_N];
int tmp[MAX_N];
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d%d", &T[i], &P[i]);
t[P[i]].push_back(i);
}
for (int i = 1; i <= n; i++) {
if (t[i].size() < 500) continue;
ma[i] = ++tot;
int f = 0;
for (int j = 1; j <= m; j++) {
if (f) tmp[j] = T[j] - T[j - 1];
else tmp[j] = 0;
if (P[j] == i) f ^= 1;
}
for (int j = 1; j <= m; j++) tmp[j] += tmp[j - 1];
for (int j = 1; j <= n; j++) {
if (i == j) continue;
for (int k = 0, l = t[j].size(); k < l;
k += 2) {
ans[tot][j] +=
tmp[t[j][k + 1]] - tmp[t[j][k]];
}
}
}
scanf("%d", &q);
int a, b, l1, l2, lt, f1, f2, p1, p2, ans2;
while (q--) {
scanf("%d%d", &a, &b);
if (ma[a]) {
printf("%d\n", ans[ma[a]][b]);
continue;
}
if (ma[b]) {
printf("%d\n", ans[ma[b]][a]);
continue;
}
p1 = p2 = ans2 = f1 = f2 = lt = 0;
l1 = t[a].size();
l2 = t[b].size();
while (p1 < l1 && p2 < l2) {
if (t[a][p1] < t[b][p2]) {
if (f1 && f2) ans2 += T[t[a][p1]] - lt;
f1 ^= 1;
lt = T[t[a][p1]];
p1++;
} else {
if (f1 && f2) ans2 += T[t[b][p2]] - lt;
f2 ^= 1;
lt = T[t[b][p2]];
p2++;
}
}
printf("%d\n", ans2);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号