二叉树

一、二叉树的性质

性质1：在二叉树的第i层上至多有2^i-1结点（i>=1）

性质2：深度为K的二叉树至多有2^K-1个结点（K>=1）

性质3：对任何一颗二叉树T，如果其终端结点数为n0,度为2的结点数为n2,则n0=n2+1。用代数的表达 分支线总数n-1=n1+2n2。而有等式n=n0+n1+n2,所以可以推导n0=n2+1.

性质4：具有n个结点的完全二叉树的深度为|log₂n|+1

二、二叉树的遍历

二叉树遍历：从树的根节点出发，按照某种次序依次访问二叉树中的所有结点，使得每个结点被访问一次且仅被访问一次。这里有两个关键词：访问和次序。

1、前序遍历

 

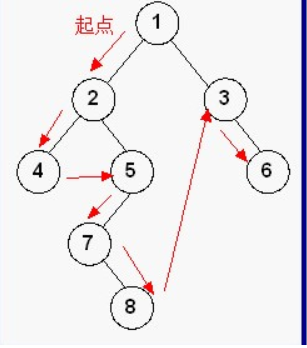
基本思想：若二叉树为空，则空操作返回，否则先访问根结点，然后前序遍历左子树，再前序遍历右子树。

public void PreOrder(BinaryNode Node) {
    if(Node!=null) {
        System.out.print(Node.element+" ");//显示结点数据
        PreOrder(Node.left);//再先先序遍历左子树
        PreOrder(Node.right);//最后先序遍历右子树
    }
}

2、中序遍历

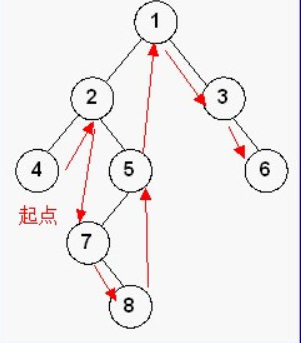
基本思想：先中序遍历左子树，然后再访问根结点，最后再中序遍历右子树，即左——根——右；

public void Inorder(Binary Node) {
    if(Node==null)
        return;
    Inorder(Node.left);
    System.out.print(Node.element+" ");
    Inorder(Node.right);
}

 

 3、后序遍历

 

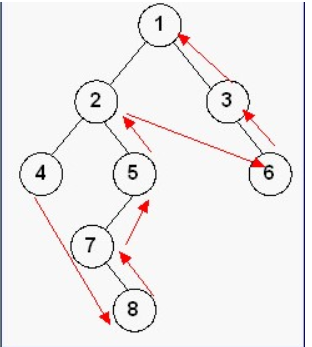
public void PosOrder(BinaryNode Node){
    if(Node==null)
        return;
    PosOrder(Node.left);
    PosOrder(Node.right);
    System.out.print(Node.element+" ");
}

 三、三种遍历的用途

1、输出某个文件夹下所有文件名称（可以有子文件夹）——先序遍历。

如果是文件夹，先输出文件夹名，然后再依次输出该文件夹下的所有文件(包括子文件夹)，如果有子文件夹，则再进入该子文件夹，输出该子文件夹下的所有文件名。这是一个典型的先序遍历过程。

 public void list(File f){
        list(f, 0);
    }
    public void list(File f, int depth){
        printName(f, depth);
        if(f.isDirectory()){
            File[] files = f.listFiles();
            for (File file : files) {
                list(file, depth + 1);
            }
        }
    }

  private void printName(File f, int depth){
        String name = f.getName();
        for(int i = 0; i < depth; i++)
            System.out.print("    ");
        if(f.isDirectory())
            System.out.println("Dir:" + name);
        else
            System.out.println(f.getName() + ":" + f.length()/1024 + "KB");
    }

 

 

2、统计某个文件夹的大小（该文件夹下所有文件的大小）——后序遍历。

 private long totalSize(File f){
        long size = 0;
        if(f.isFile())
        {
            size = f.length();
        }
        else
        {
            File[] files = f.listFiles();
            for (File file : files) {
                size += totalSize(file);
            }
        }
        return size;
    }

 

若要知道某文件夹的大小，必须先知道该文件夹下所有文件的大小，如果有子文件夹，若要知道该子文件夹大小，必须先知道子文件夹所有文件的大小

附上完整程序：

package com.sxj.Bianli;
import java.io.File;

public class FileList {
    public void list(File f){
        list(f, 0);
    }
    public void list(File f, int depth){
        printName(f, depth);
        if(f.isDirectory()){
            File[] files = f.listFiles();
            for (File file : files) {
                list(file, depth + 1);
            }
        }
    }
    
    private long totalSize(File f){
        long size = 0;
        if(f.isFile())
        {
            size = f.length();
        }
        else
        {
            File[] files = f.listFiles();
            for (File file : files) {
                size += totalSize(file);
            }
        }
        return size;
    }
    
    /**recursive error
    private long totalSize(File f, long size){
        if(f.isFile())
        {
            size += f.length();
        }
        else
        {
            File[] files = f.listFiles();
            for (File file : files) {
                size += totalSize(file, size);
            }
        }
        return size;
    }
    */
     private void printName(File f, int depth){
        String name = f.getName();
        for(int i = 0; i < depth; i++)
            System.out.print("    ");
        if(f.isDirectory())
            System.out.println("Dir:" + name);
        else
            System.out.println(f.getName() + ":" + f.length()/1024 + "KB");
    }
     
     public static void main(String[] args) {
        FileList flist = new FileList();
        File f = new File("F:\\体育部");
        flist.list(f);
        
        long size = flist.totalSize(f);
        System.out.println(size/1024/1024 + "MB");
    }
}

 

3、中缀表达式转为后缀表达式。

假设一个表达式，a+b*c+d-e/f，利用将其存储在二叉树中，保持中序遍历得到中缀表达式。