浮点数的表示及其范围的理解

参考 https://zhuanlan.zhihu.com/p/400006735 （就是对着梳理了一遍）

首先，数在机器里有四种表示：原码、反码、补码、移码

对于一个正数，其原码、反码、补码相同，移码是补码的符号位取反
对于一个负数：
反码：由原码按位取反
补码：由原码按位取反+1
移码：其补码的符号位取反

已知【x】补码，【-x】的补码是其所有位按位取反+1

定点数据表示

举例我们以8位长度数据为例

定点整数

原码表示

其数轴是对称的，0在原码中有两种表示形式

最大正数：\(2^{n-1}-1\) 0111 1111

最小正数：\(1\)

最大负数：\(-1\)

最小负数：\(-(2^{n-1}-1)\)

补码表示

其正数的表示范围并没有变化，但最小负数变为\(-2^{n-1}\) (这一点非常重要)
0只有一种表示形式。

最大正数：\(2^{n-1}-1\) 0111 1111

最小正数：\(1\)

最大负数：\(-1\)

最小负数：\(-2^{n-1}\)

所以补码的表示范围为 \(-2^{n-1}\)~\(2^{n-1}-1\)

定点小数

原码表示

最高位表示符号位

0的表示方式仍然有两种

最大正数：\(1-2^{-(n-1)}\) 0.1111 1111+0.0000 0001==1.0000 0000

最小正数：\(2^{-(n-1)}\)

最大负数：\(-2^{-(n-1)}\)

最小负数：\(-(1-2^{-(n-1)})\)

补码表示

0只有一种表示形式

最大正数：\(1-2^{-(n-1)}\)

最小正数：\(2^{-(n-1)}\)

最大负数：\(-2^{-(n-1)}\)

最小负数：\(-1\)

所以补码表示范围 \(-1\)~\(1-2^{-(n-1)}\)

浮点数表示

浮点数表示法是指以适当的形式将比例因子表示在数据中，让小数点的位置根据需要而浮动。这样，在位数有限的情况下，既扩大了数的表示范围，又保持了数的有效精度。

一般格式表示（非规格化）

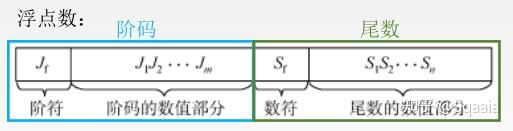
阶码的数值位数为m，尾数的数值部分位数为n

数的真值：\(N=r^E*M\)

\(r：阶码的底，通常为2\)

\(E：阶码数值，决定数的范围\)

\(M：尾数，决定数的符号和精度\)

原码表示：

对于正数而言：

\(E\) 的最大值为：\(2^m-1\)

\((m位二进制数的最大值每位都是1，表示的是2^m-1)\)0111 0为阶符

\(E\) 的最小值为：\(-(2^m-1)\) 1111

\(M\) 的最大值为：\(1-2^{-n}\) 0.111

\(M\) 的最小值为：\(2^{-n}\) 0.001

所以\(N\)的最大值为：\(r^{2^m-1}*(1-2^{-n})\)，01110111

\(N\)的最小值为：\(r^{-(2^m-1)}*(1-2^{-n})\),11110001

对于负数而言：

\(E\) 的最大值为：\(2^m-1\) ,0111

\(E\) 的最小值为：\(-(2^m-1)\) 1111

\(M\) 的最大值为：\(-2^{-n}\) 1.001

\(M\) 的最小值为：\(-(1-2^{-n})\) 1.111

所以\(N\)的最大值为：\(-r^{-{(2^m-1)}}*(2^{-n})\)，1111 1001(让阶码以及尾数的绝对值尽量小)

所以\(N\)的最大值为：\(-r^{{(2^m-1)}}*(1-2^{-n})\)，0111 1111(让阶码以及尾数的绝对值尽量大)

补码表示：

对于正数而言：

\(E\) 的最大值为：\(2^m-1\)0111

\((m位二进制数的最大值每位都是1，表示的是2^m-1)\)0111 0为阶符

\(E\) 的最小值为：\(-2^m\) 1000

\(M\) 的最大值为：\(1-2^{-n}\) 0.111

\(M\) 的最小值为：\(2^{-n}\) 0.001

所以\(N\)的最大值为：\(r^{2^m-1}*(2^{-n})\)，01110111（注意这里与上述的不一样）

对于负数而言：

\(E\) 的最大值为：\(2^m-1\) 0111

\(E\) 的最小值为：\(-2^m\) 1000

\(M\) 的最大值为：\(-2^{-n}\) 1.111

\(M\) 的最小值为：\(-1\) 1.000

所以\(N\)的最大值为：\(-r^{-{(2^m)}}*(2^{-n})\)，1000 1111(让阶码以及尾数的绝对值尽量小)

所以\(N\)的最小值为：\(-r^{{(2^m-1)}}\)，1000 1000(让阶码以及尾数的绝对值尽量大)

规格化表示

规格化指的是：尾数的数值位最高位必须是一个有效值，它的定义是：在浮点数中，为了在尾数中表示最多的有效数据位，同时使浮点数具有唯一的表示方式，浮点数的编码应当采用一定的规范，规定尾数部分用纯小数给出，而且尾数的绝对值应大于或等于1/R，并小于或等于1，即小数点后的第一位不为零。这种表示的规范称为浮点数的规格化的表示方法。不符合这种规定的数据可通过修改阶码并同时移动尾数的方法使其满足这种规范。

也就是在原码下尾数必须是 X.1XXX...XXX这种形式，并且当尾数不是这种形式时必须对其进行移位处理且伴随着阶码的改变，同时在补码下尾数必须是0.1XXXXX..X.或者 1.0XXXXX..X 这种形式

这一点相当重要，理解补码的规格化

补码表示

以补码形式保存的尾数

对于正数，规定必须是0.1XXXXX..X这种形式

对于负数，规定必须是1.0XXXXX..X这种形式

对于正数而言：

\(E\) 的最大值为：\(2^m-1\)0111

\((m位二进制数的最大值每位都是1，表示的是2^m-1)\)0111 0为阶符

\(E\) 的最小值为：\(-2^m\) 1000 （注意此处范围扩大了）

\(M\) 的最大值为：\(1-2^{-n}\) 0.111

\(M\) 的最小值为：\(1/2\) 0.100

所以\(N\)的最大值为：\(r^{(2^{m}-1)}*(1-2^{-n})\)，0111 0111(让阶码以及尾数的绝对值尽量小)

所以\(N\)的最小值为：\(-r^{{(2^m)}}*1/2\)，1000 0100(让阶码以及尾数的绝对值尽量大)

对于负数而言

\(E\) 的最大值为：\(2^m-1\)0111

\((m位二进制数的最大值每位都是1，表示的是2^m-1)\)0111 0为阶符

\(E\) 的最小值为：\(-2^m\) 1000 （注意此处范围扩大了）

\(M\) 的最大值为：\(-(1/2+2^{-n})\) 1.011其原码1.101

\(M\) 的最小值为：\(-1\) 1.000

所以\(N\)的最大值为：\(r^{(2^{m}-1)}*(1-2^{-n})\)，0111 0111(让阶码以及尾数的绝对值尽量小)

所以\(N\)的最小值为：\(-r^{{(2^m)}}*1/2\)，1000 0100(让阶码以及尾数的绝对值尽量大)

注意此处：

M的最大值不为1/2，若为1/2则其补码为1.100，不符合负数规格化补码规范

• 要想取补后是1.0XXXXX..X那么原码必须是1.1XXXXX..X这样的格式
• 由于·1.100000..0取补后仍为其本身，所以它不能当作最大的负尾数
• 所以最大的负尾数应该在最末尾加上一个1，为1.10000...1，取补后为1.0111111...1 这种类型

所以\(N\)的最大值为：\(r^{(2^{m})}*(1/2+2^{-n})\)，1000 1011(让阶码以及尾数的绝对值尽量小)

所以\(N\)的最小值为：\(-r^{{(2^m-1)}}*1/2\)，0111 1000(让阶码以及尾数的绝对值尽量大)