关于全排列算法

首先介绍：邻位互换算法

原理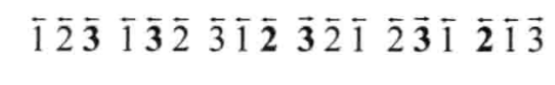：首先会先给数据排序（从小到大），然后给这些数据赋上移动数据，比如最开始都给他们赋值为-1表示能向左移，其实在这里只用一个新数组来存储移位数据就可以了，比如我们现在3是可以左移的，3的位置是2，然后通过去找移位数组里面的值，发现对于位置2的值为-1，只用拿2-1就可以得到，3移位后的位置了。

 

 

其次如果3移动到最左边就不能再移位了，这个时候要去找剩余元素里面最大的元素，通过移动它一次，然后再改变3的移动方向，继续移位。（注意移动方向的元素，必须要小于移动元素）最后会发现都不能再移动了。

上代码：

# include <cstdio>
# include <algorithm>
# include <cstring>
# include <cmath>

using namespace std;

const int N_MAX = 10;

int n;
int a[N_MAX + 10];
int face[N_MAX + 10];

bool canMove(int x)
{
	int y = x + face[x];
	return y >= 1 && y <= n && a[x] > a[y];//判断移位是否已经到达边界，并且移动的下一个元素要小于此时移动的元素
}

bool permutation()
{
	int a_max = 0, pos = -1;
	for (int i = 1; i <= n; i++) {
		if (!canMove(i) || a_max > a[i]) continue;
		a_max = a[i], pos = i;
	}
	if (pos == -1) return false;
	int pos_to = pos + face[pos];
	swap(a[pos], a[pos_to]);
	swap(face[pos], face[pos_to]);//！！！很重要，元素头上那个箭头要跟着元素移动哦
	for (int i = 1; i <= n; i++)
		if (a[i] > a_max) face[i] = -face[i];
	return true;
}

int main()
{
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
		a[i] = i;
	memset(face, -1, sizeof(face));
	do {
		for (int i = 1; i <= n; i++)
			printf("%5d", a[i]);
		printf("\n");
	} while (permutation());
	return 0;
}

 递归实现算法：

原理：比如现在我们有一个数组{1，2，3，4}要求它的全排列，其实可以想象为先求首元素是1的2，3，4的全排列，然后首元素为2的1，3，4的全排列。。。。。。

2，3，4的全排列又可以想象成去求首元素是2的3，4的排列，依次减治下去！！！

上代码：

#include <stdio.h> 

int n = 0;                            //n用来计全排列的总数
int main()                         //主函数
 {   int list[] = {3,5,8,2};    
     perm(list, 0, 3);
     printf("total:%d\n", n);     //输出n的个数
    
 } 


void perm(int list[], int begin, int end)      //产生list[begin:end]的所有排列
 {    
     int i;    
     if  (begin == end)        //begin等于end，即list中只有一个元素时
     {         
         for(i = 0; i <= begin; i++)            
             printf("%d ", list[i]);         //打印出这个排列
         printf("\n");        
         n++;                 //n的个数加一，表示又有一种情况产生了
     }    
     else    
     {        
         for(i = begin; i <= end; i++)   
         {            
             swap(&list[begin], &list[i]);             
             perm(list, begin + 1, end);            
             swap(&list[begin], &list[i]);        //必须要在递归下去的时候将已经移位的数据进行还原，比如1，2，3，4你进行到了2，3交换的时候，然后进入递归此时数组为1，3，2，4就只用再交换2，4就行了，然后退回到递归之前，这个时候你要还原数组为1，2，3，4这时2，就会和4交换。因此所有情况都会遍历
         }    
     }
 }

void swap(int *a, int *b)           //用来交换两个变量值的函数
 {    
     int m;    
     m = *a;    
     *a = *b;    
     *b = m;
 }