匈牙利算法
通过数代人的努力,你终于赶上了剩男剩女的大潮,假设你是一位光荣的新世纪媒人,在你的手上有N个剩男,M个剩女,每个人都可能对多名异性有好感( -_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉
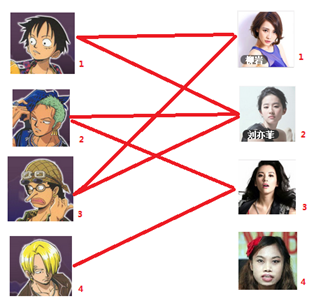
-_-||暂时不考虑特殊的性取向),如果一对男女互有好感,那么你就可以把这一对撮合在一起,现在让我们无视掉所有的单相思(好忧伤的感觉 ),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
),你拥有的大概就是下面这样一张关系图,每一条连线都表示互有好感。
本着救人一命,胜造七级浮屠的原则,你想要尽可能地撮合更多的情侣,匈牙利算法的工作模式会教你这样做:
===============================================================================
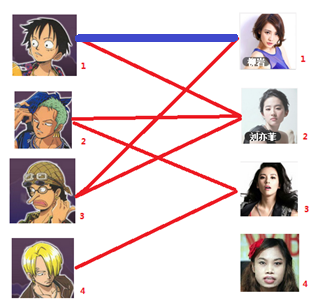
一: 先试着给1号男生找妹子,发现第一个和他相连的1号女生还名花无主,got it,连上一条蓝线
===============================================================================
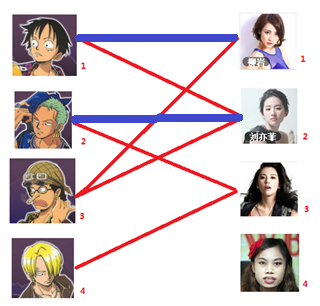
二:接着给2号男生找妹子,发现第一个和他相连的2号女生名花无主,got it
===============================================================================
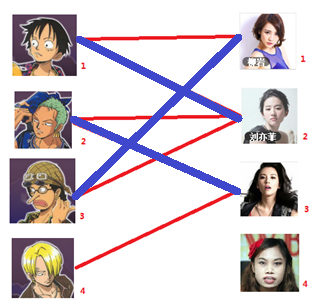
三:接下来是3号男生,很遗憾1号女生已经有主了,怎么办呢?
当在给第三个男生找妹子的时候,我们也是对妹子进行一个循环找,先重第一个开始找,但是找到第一个女生,发现她已经心有所属了,所以我们直接断绝她和1号男生的来往,让1号男生再去找另一个女生,就找到了2号女生,但是2号女生这个时候又和2号男生联系了,所以我们也断开他们的来往,让2号男生去找他的下一个妹子,所以2会与三号妹子联系。
所以第三步最后的结果就是:
===============================================================================
四: 接下来是4号男生,很遗憾,按照第三步的节奏我们没法给4号男生腾出来一个妹子,我们实在是无能为力了……香吉士同学走好。
===============================================================================
这就是匈牙利算法的流程,其中找妹子是个递归的过程,最最关键的字就是“腾”字
其原则大概是:有机会上,没机会创造机会也要上
来上代码!!!
// 定义需要的变量
#define N 205
#define M 205
bool line[N][M]; //表示对应位置的奶牛和畜栏是否有边
int hascow[M]; //表示对应位置的畜栏被分配到哪一只编号的奶牛(0是未分配)
bool used[M]; //表示对应位置的畜栏是否已经被走过了,用于确保寻求增广路不走重复结点
int n, m;
复制代码
复制代码
//分配
bool find(int x) {
for (int i=1; i<=m; i++) { //遍历所有畜栏
//如果该奶牛可以分配到这个畜栏并且该畜栏未被使用
if (line[x][i] && !used[i]) {
used[i] = true; //标记该畜栏当前循环被使用了,而且你还要注意的是,当我们再进行递归的时候,如果下次函数又找到它,这个时候其实他是已经被标记了的,所以不会再考虑它,i继续加,去找下一个和他匹配的。
//如果该畜栏没有被分配或者可以通过给原本占有该畜栏的奶牛分配其它畜栏
if (!hascow[i] || find(hascow[i])) {
//将该畜栏分配给该奶牛
hascow[i] = x;
return true; //分配成功
}
}
}
return false; //分配失败
}
复制代码
复制代码
int main() {
int t, x, res;
while (~scanf("%d%d", &n, &m)) {
//初始化变量,然后根据输入格式构建二分图
memset(line, 0, sizeof(line));
for (int i=1; i<=n; i++) {
scanf("%d", &t);
for (int j=1; j<=t; j++) {
scanf("%d", &x);
line[i][x] = true;
}
}
res = 0;
memset(hascow, 0, sizeof(hascow));
for (int i=1; i<=n; i++) {
memset(used, 0, sizeof(used));
if (find(i)) res ++; //如果可以成功给该奶牛分配畜栏,可以分配的奶牛数量+1
}
printf("%d\n", res);
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号