背包问题

背包问题概述：有n个物品，它们有各自的体积和价值，现有给定容量的背包，如何让背包里装入的物品具有最大的价值总和？

如果按照蛮力法去算的话复杂度会很高，大概是2^n次，因此不会用蛮力法。

在这里可以依据动态规划的思想来做这个。

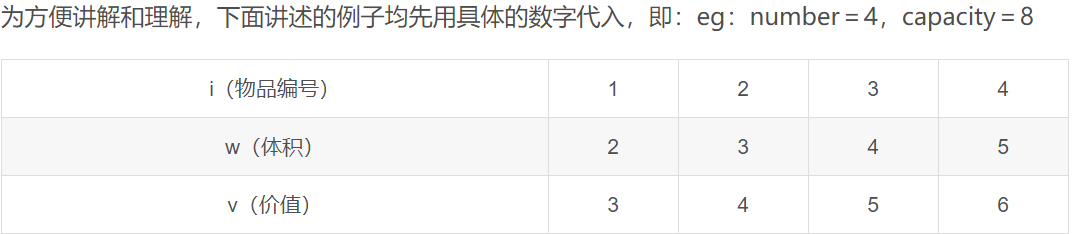
首先规定i代表第几个物品，j代表体积。Vi代表第i个物品的价值，Wi代表第i个物体的体积。V(i,j)代表当前背包容量是j，前i个物品的最佳组合方式（可能你在这儿会有疑问，为什么我就这么肯定他是最佳组合呢？你可以先留下这个疑惑，去看看后面的规划表是如何生成的可能就会恍然大悟了）。

！！！要明白两个式子：1.j<w(i) V(i,j)=V(i-1,j);代表如果j小于了此时要装进来的物体的体积，那我们就不装（因为j是现在背包的容量）所以现在背包的价值就和上面没有装i的价值是一样的，因为我们没有装i。

2.j>w(i)  V(i,j)=max{V(i-1,j),V(i-1,j-w(i))+v(i)};代表如果放入第i个物体时，如果i的体积小于背包体积j。说明物体i可以放进去，但是我们怎么放呢？这里要强调最大收益哦？所以我们i-1,j-w(i)就是留出1个位置，然后背包容量也减去这个位置要占的容量，回溯到i-1那里去看看，那的背包方成什么样了，我们只用在他基础上跟着放就ok了。（为什么要回溯呢？其实很好理解，因为我们每次在构建V（i，j）的时候都是在算他的最大收益，所以回溯回去看之前i-1时是怎么放的，知道了后我们只用放入我们现在需要放入的物体就行了，保证每次都是最优值）

可能在这里，你还是有点不懂这个式子，没事。。你继续往下看，这个是规划表构成的规定。

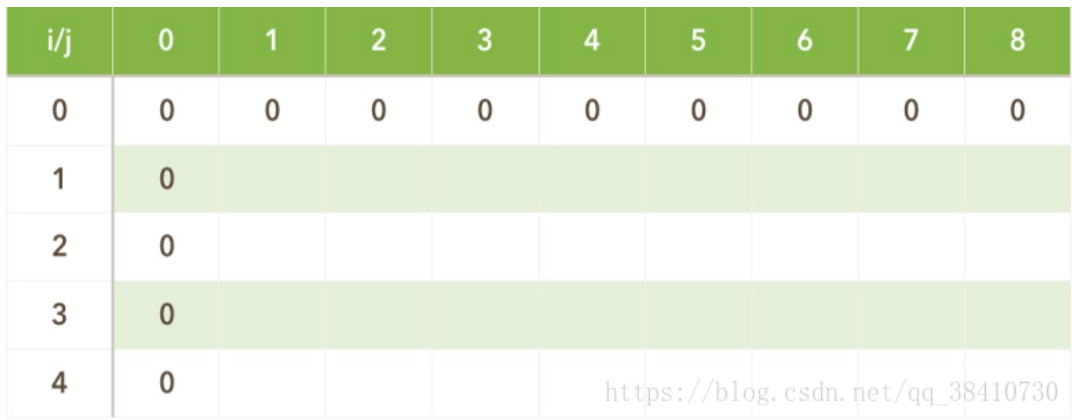j=0时，说明背包容量为0，因此V(i,0)=0(代表任意时候背包价值)。i=0时，放第0个元素，因为我们没有第0个物体要放，此时背包价值也为0。

 

有人问为什么要先给规划表赋初值，那我反问你，如果你在算i=1时，如果j<w(i) V(i,j)=V(i-1,j)，那V(i-1,j)等于啥？

初始化我们的规划表，规划表的作用就是从最开始i=1,j=1开始每个环节的最优解，然后从下到上，每次都是拿最优解来操作，最后得到的也是最优解。

 

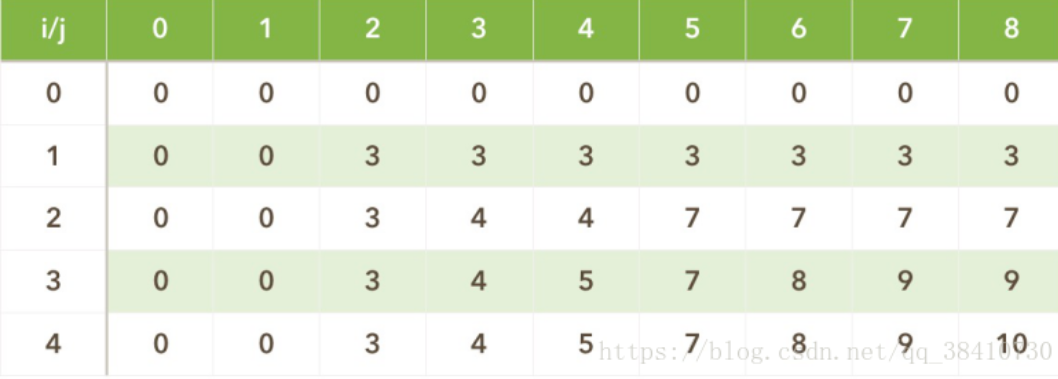
 举个例子，比如我们看i=2，j=5的时候，说明现在放入第2个物体，并且背包容量是5。我们这个时候第二个物体积是3，价值是4。现在j>3说明可以放进去，那我们就要回去看放第一个物体时并且背包容量时2时的最优解是什么。为什么是看第一个物体，背包容量是2的情况呢？首先放置第二个物体的体积是3，然后现在背包容量是5，那我们还能用的体积是不是2.所以i-1回到前面去看之前的最优解。i=1,j=2的最优解是3，说明可以放入第一个物体。因此加起来就可以，所以得出i=2,j=5的情况最优解是7.

现在规划表出来了，有了最优解，那我们怎么去求出这个最优解的组成呢？

 

 其实就是根据我们构造最优解的方法来回溯。

举个例子：最优解为V(4,8)=10，而V(4,8)!=V(3,8)却有V(4,8)=V(3,8-w(4))+v(4)=V(3,3)+6=4+6=10，所以第4件商品被选中，并且回到V(3,8-w(4))=V(3,3)；

到这里方法就讲完了，具体代码呈上！！！

#include<iostream>
using namespace std;
#include <algorithm>

int w[5] = { 0 , 2 , 3 , 4 , 5 }; //商品的体积2、3、4、5
int v[5] = { 0 , 3 , 4 , 5 , 6 }; //商品的价值3、4、5、6
int bagV = 8; //背包大小
int dp[5][9] = { { 0 } }; //动态规划表
int item[5]; //最优解情况

void findMax() { //动态规划
for (int i = 1; i <= 4; i++) {
for (int j = 1; j <= bagV; j++) {
if (j < w[i])
dp[i][j] = dp[i - 1][j];
else
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
}
}
}

void findWhat(int i, int j) { //最优解情况
if (i > 0) {
if (dp[i][j] == dp[i - 1][j]) {
item[i] = 0;
findWhat(i - 1, j);
}
else if (j - w[i] >= 0 && dp[i][j] == dp[i - 1][j - w[i]] + v[i]) {
item[i] = 1;
findWhat(i - 1, j - w[i]);
}
}
}

void print() {
for (int i = 0; i < 5; i++) { //动态规划表输出
for (int j = 0; j < 9; j++) {
cout << dp[i][j] << ' ';
}
cout << endl;
}
cout << endl;

for (int i = 0; i < 5; i++) //最优解输出
cout << item[i] << ' ';
cout << endl;
}

int main()
{
findMax();
findWhat(4, 8);
print();

return 0;
}