关于用矩阵来求斐波拉契数列问题详解

首先要明确什么是斐波拉契数列即：除了第一个和第二个元素1，1外，后面剩余的元素都是前两个元素相加得来的。

1、1、2、3、5、8、13、21、34。。。。。。

为什么能用矩阵来求斐波拉契数列呢？

首先看看这个矩阵相乘

 

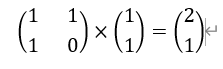可以把右边的矩阵看作是前第二个和第一个斐波拉契数列数组成的，因此乘了左边那个矩阵就会变成最终的结果，可以看成第3个数和第2个数组成的数列。

 

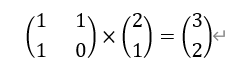如果再用左边这个数列去乘上面产生的结果，又会产生第4个和第3个斐波拉契数列数构成的矩阵。

 

看到这，就会有规律了，其实就是要得到第几个斐波拉契数列的数其实就是看乘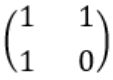的几次方。

 

现在的问题是如何去求矩阵相乘和矩阵的幂呢？

首先要了解快速幂这个思想。

比如b^11次方如何求，其实可以先把11转换为二进制1011.然后通过位与的方式来求。

例子：

 

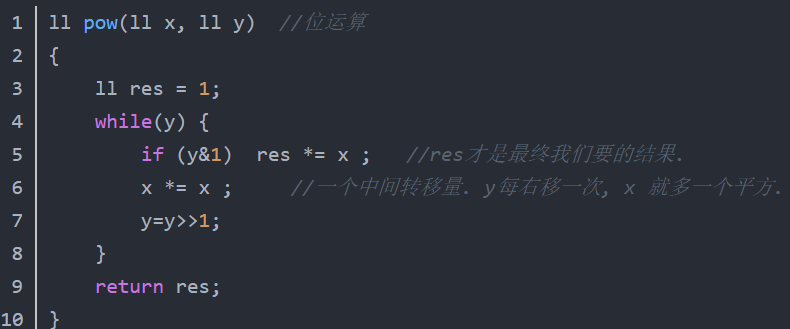
然后通过这个快速幂的思想我们首先要明确矩阵乘法怎么做，然后对其再使用快速幂

 

 

 

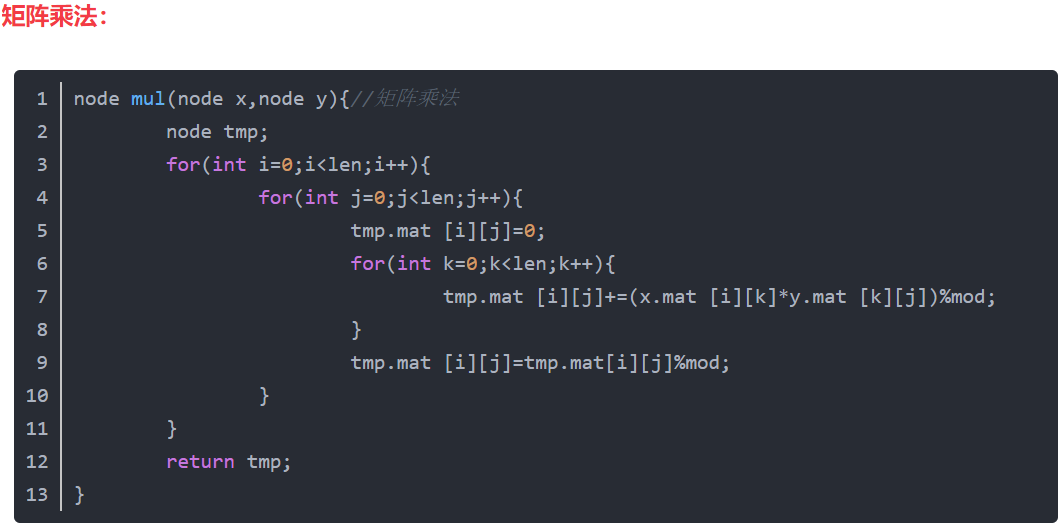
 这引入K的做法是因为，在第一列和第一行元素相乘相加时，行上的元素行没有变，只有列变了，列上元素列没有变，只有行变了，所以i，j就是没有变的，而k在改变。

 

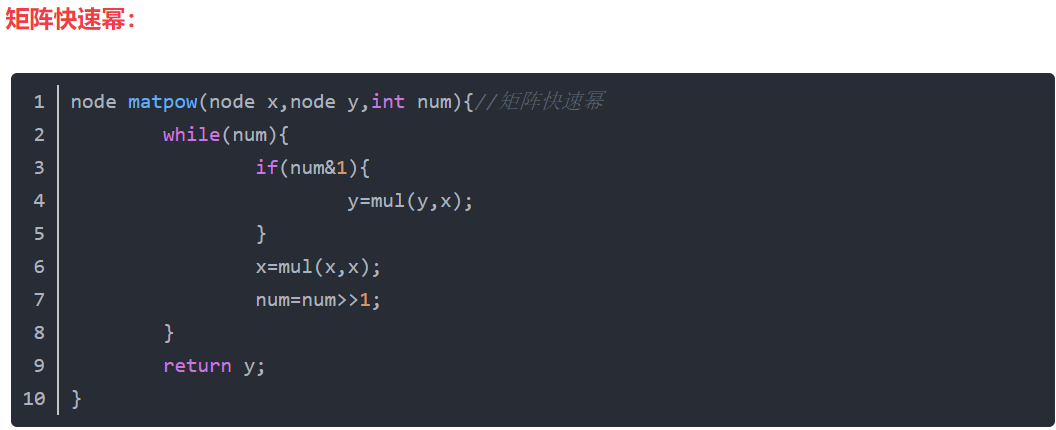
 到这儿就可以求出矩阵的幂了然后求出斐波拉契数列具体位置上的数。