莫队专题（未完待续）

普通莫队

适用范围

• 问题支持离线。
• 没有修改只有查询。
• 可以从任意状态下的答案推导到相邻状态的答案并所花时间较少。
• 具体的，能从 \(\left[ l, r \right]\) 的答案推导出 \(\left[ l + 1, r \right]\)、\(\left[ l, r - 1 \right]\)、\(\left[ l - 1, r \right]\)、\(\left[ l, r - 1 \right]\) 的答案。

原理

双指针，记 \(\left[ l, r \right]\) 为当前区间，\(p\) 为当前区间的答案。

遍历到第 \(i\) 个询问时，将 \(\left[ l, r \right]\) 通过增加或删除操作得到 \(\left [ L_i, R_i \right]\) 并得到对应的 \(p\)。

不断重复以上过程。

可以先将所有的询问排序节省部分复杂度。

但是这个过程仍然并不优秀。

如何理解不优秀？

将所有的询问排序后放到坐标轴上：

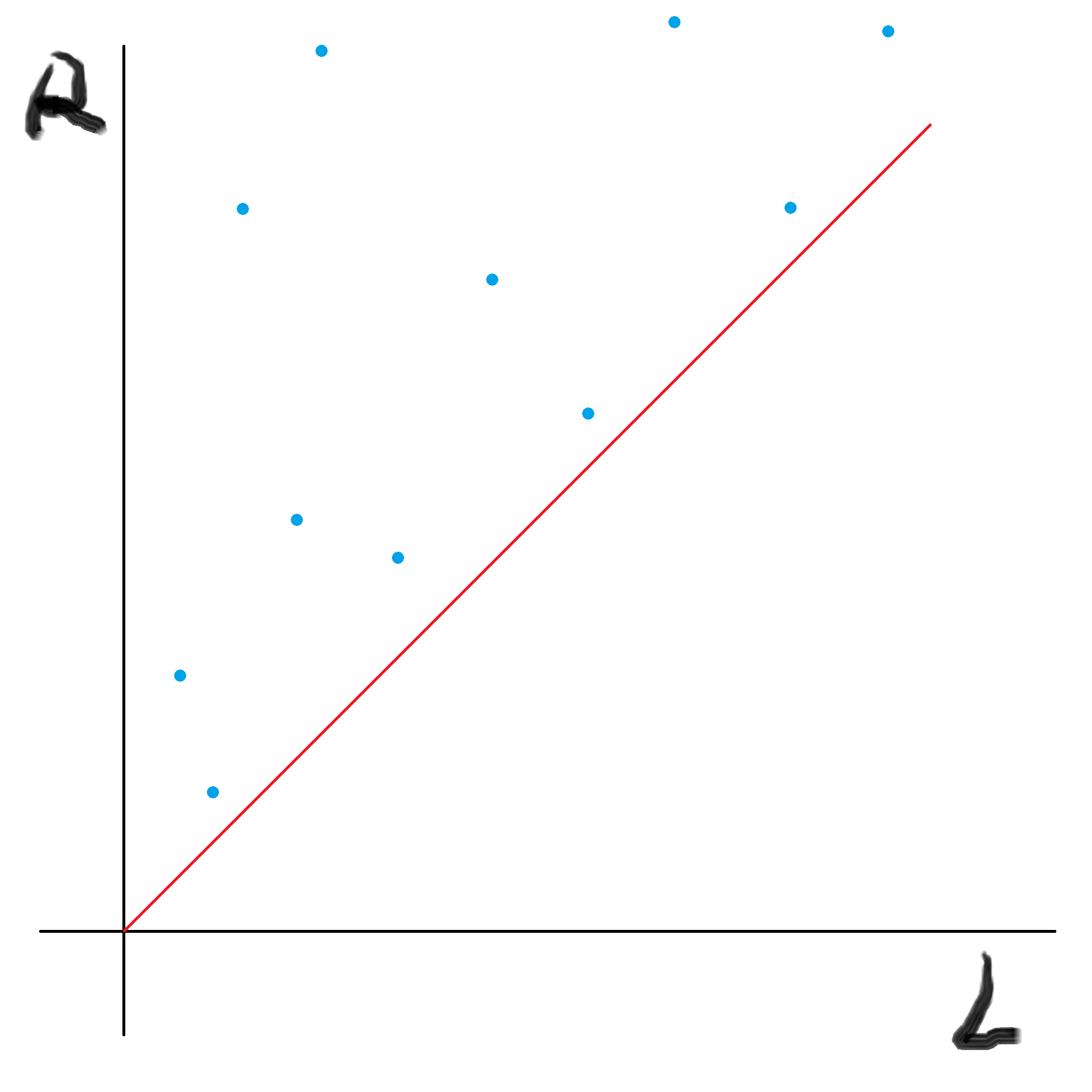
直接这么做的话可以这么表示：

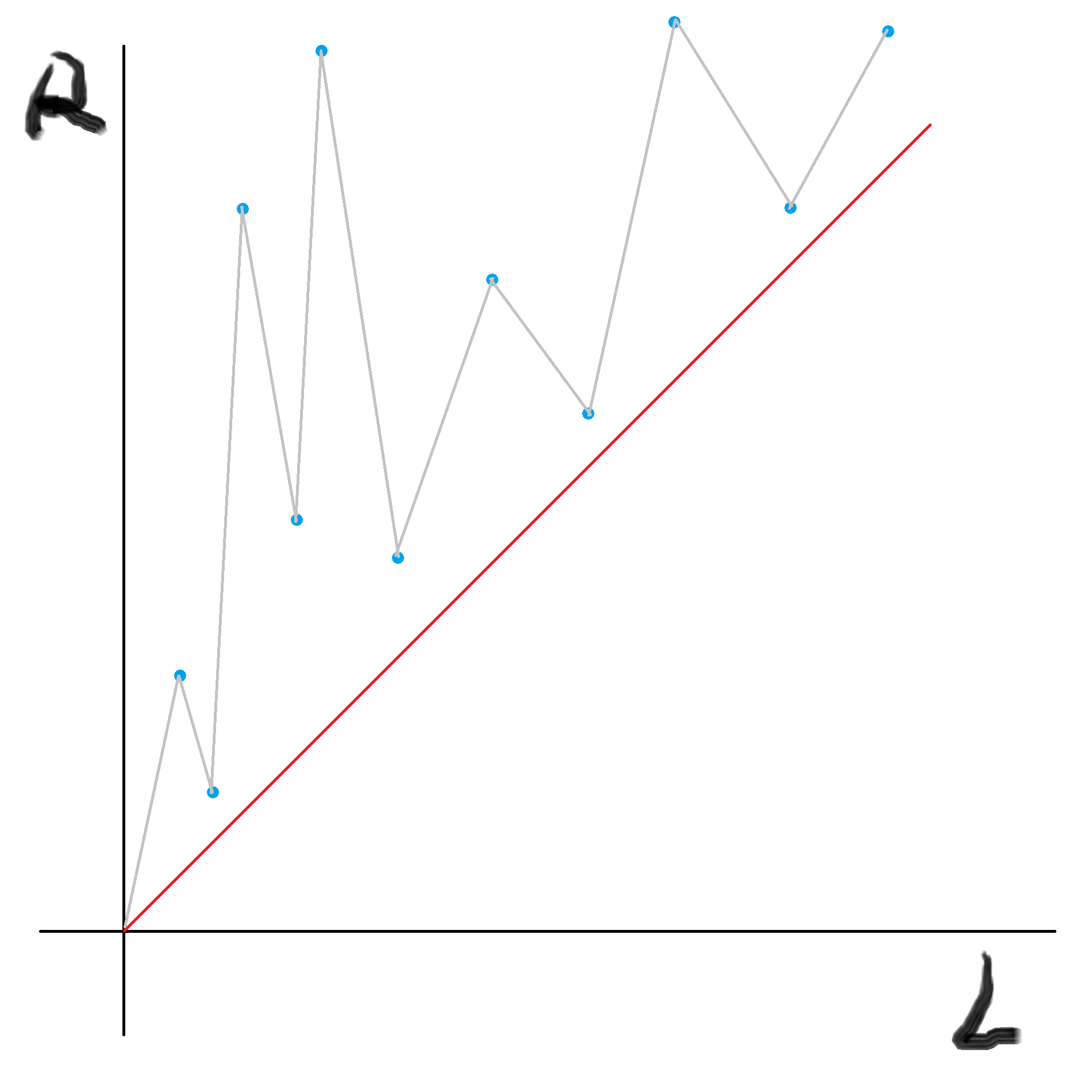
（实际上应该是曼哈顿距离，但这样看更直观）

可见上上下下不怎么优秀，浪费了很多时间。

每次上下都可以是 \(\mathcal{O}(n)\) 的复杂度，而一共 \(m\) 组上下，则时间复杂度 \(\mathcal{O}(nm)\)。

优化 \(1\)：分块

虽然这种算法的时间非常肥雾，但我们可以用这种方法加以优化。

将下标分块，块长为 \(b\)，块内按 \(r\) 排序，块外按照 \(l\) 的块编号排序。

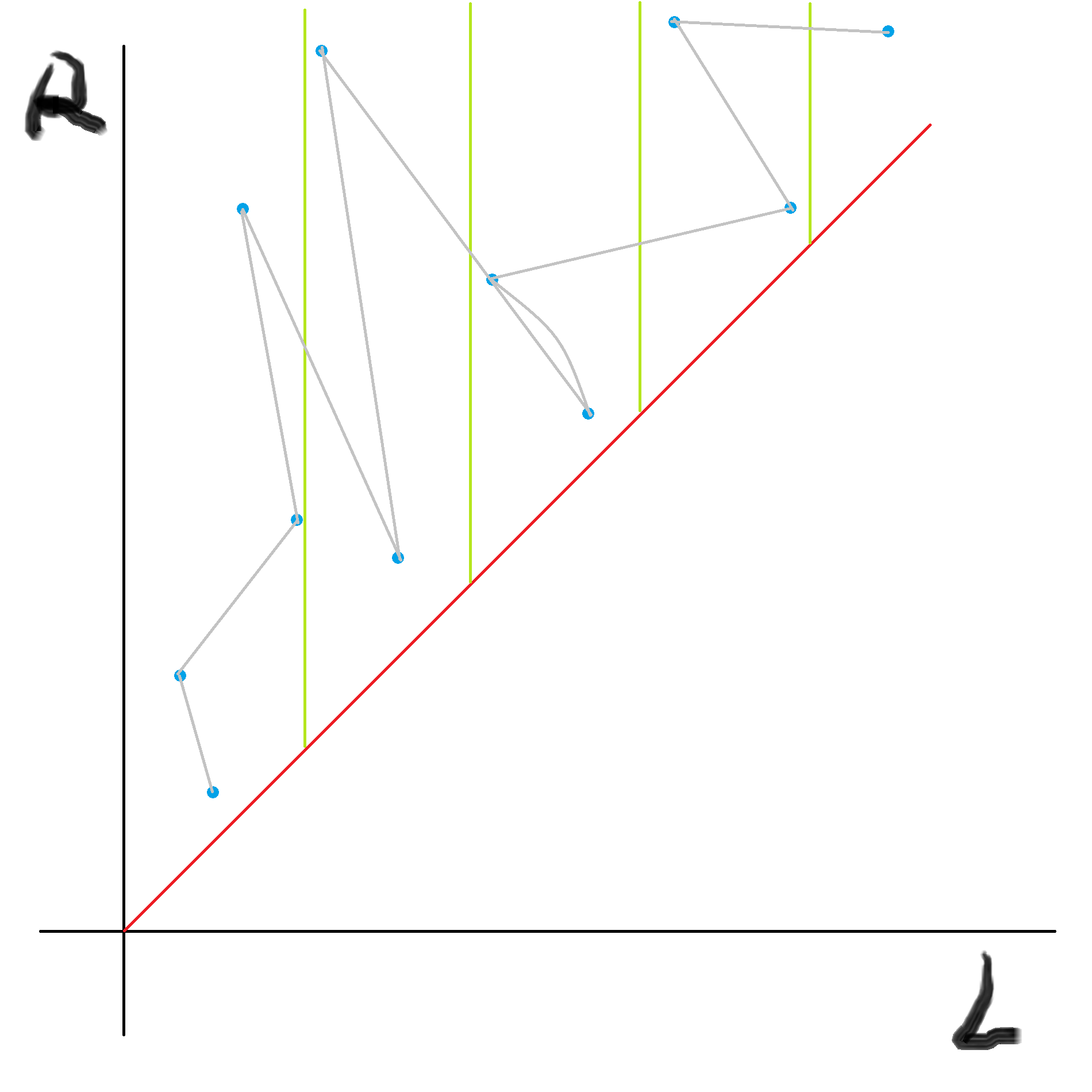
复杂度分析

设 \(n\) 为序列长度，\(m\) 为查询次数。

• 右端点指针 \(r\)：每个块内移动复杂度是 \(\mathcal O(n)\)，而一共 \(\frac{n}{b}\) 个块，则复杂度为 \(\mathcal O (\frac{n^2}{b})\)。
• 左端点指针 \(l\)：每个块内移动 \(m\) 次，共 \(b\) 个块，复杂度 \(\mathcal{O}(mb)\)。

则共 \(\mathcal{O}(\frac{n^2}{b}+mb)\)。

根据均值不等式：

\[\frac{n^2}{b}+mb\ge 2\sqrt{\frac{n^2}{b} \times mb} = 2n\sqrt{m} \]

复杂度为 \(\mathcal O (n \sqrt m)\)（\(\mathcal O (n ^ \frac{3}{2})\)），此时块长为：

\[\frac{n^2}{b} = mb \]

\[\frac{n^2}{m} = b^2 \]

\[b = \frac{n}{\sqrt{m}} \]

优化 \(2\)：奇偶优化

观察到分块后每个块都要从最低的开始，非常不优雅，于是我们可以干脆让偶数块从上往下走，此时又能省掉不少常数，如：

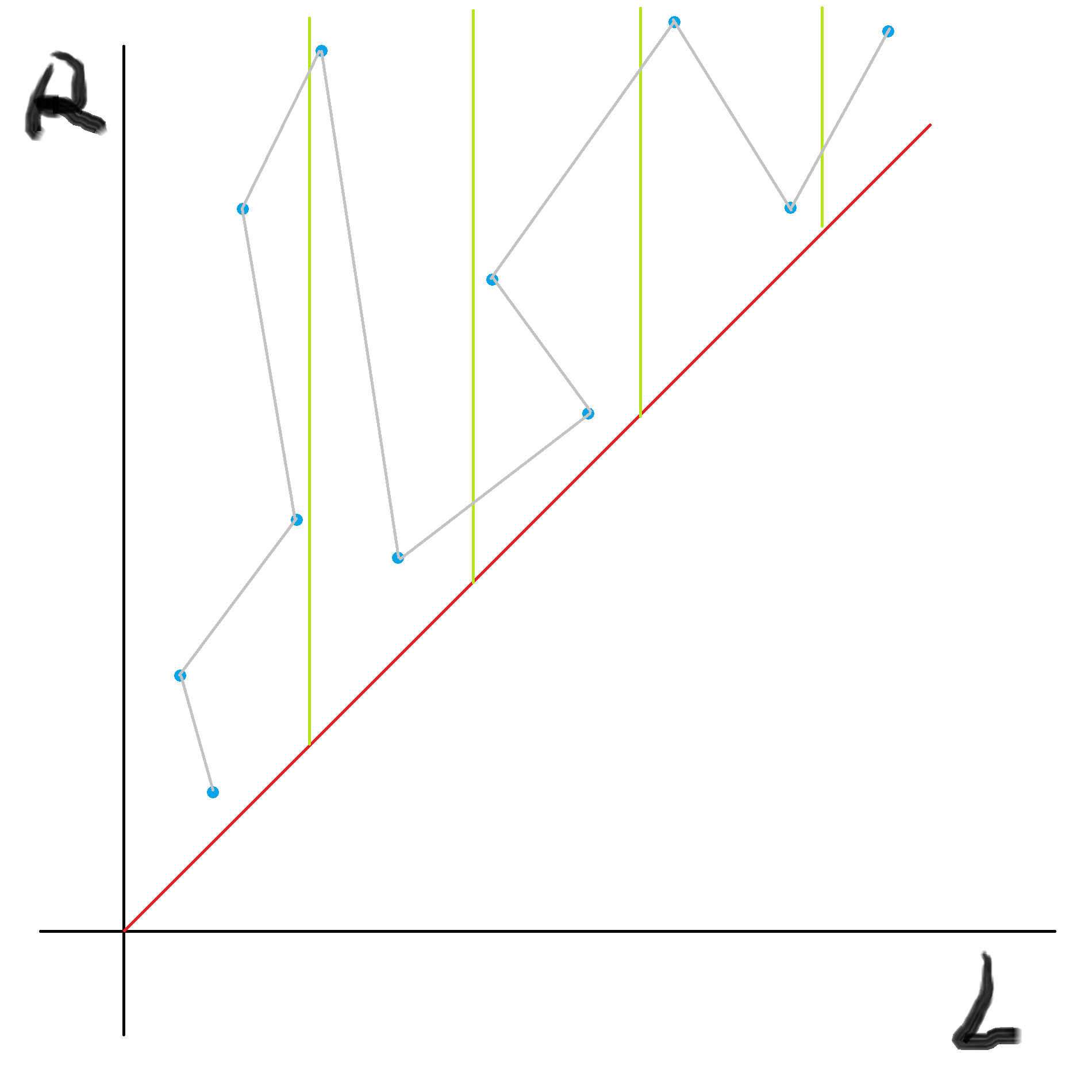
这只是常数优化，并没有对复杂度有影响。

代码

核心代码：

int l = 1, r = 0;
for (int i = 1; i <= m; i++) {
	while (r < q[i].r) add(++r);
	while (l > q[i].l) add(--l);
	while (r > q[i].r) del(r--); 
	while (l < q[i].l) del(l++);
	ans[q[i].id] = res;
}

排序规则读者可以通过上文的描述自行推导。

带修莫队

由于不带修的莫队很别扭，所以版本更迭了。

原理

如果只考虑查询的话那么跟普通莫队是肯定完全相同的。

修改可以通过增加一维时间戳来解决。

每一次查询部分移动完指针 \(l,r\) 之后，再移动一个指针 \(t\)（代表当前一共完成了前 \(t\) 次修改）到该查询的对应位置。

此时莫队就支持修改了。

排序方法

由于是三维莫队（时间戳可看作第三维），我们可以通过分析普通莫队的方法得出以下结论：

对整个序列分块，块长为 \(b\)。

• 先按左端点所在块编号排序。
• 再按右端点所在块编号排序。
• 最后按时间戳排序。

复杂度分析

设 \(n\) 为序列长度，\(m\) 为查询次数，\(k\) 为修改次数。

• 时间轴 \(t\)：每个 \(r\) 块中，最坏会移动 \(k\) 次，共 \(\left(\frac{n}{b}\right)^2 = \frac{n^2}{b^2}\) 个 \(r\) 块，则共 \(\frac{n^2k}{b^2}\) 次。
• 左端点指针 \(l\)：同普通莫队 \(mb\) 次。
• 右端点指针 \(r\)：跨 \(l\) 块时同普通莫队为 \(\frac{n^2}{b}\)，跨 \(r\) 块为 \(mb\) 次。

共 \(\mathcal O (\frac{n^2k}{b^2} + mb + \frac{n^2}{b})\)。

\[\begin{align*} f(b) &= \frac{n^2k}{b^2} + mb + \frac{n^2}{b} \\ &= \frac{n^2k+n^2b}{b^2} + mb \\ &= \frac{(k + b) \times n^2}{b^2} + mb \\ &= (b + k) \times \left(\frac{n}{b}\right)^2 + mb \end{align*} \]

要为这个公式算最小值，可以用求导的方法。

\[\begin{align*} f^{\prime}(b) &= \frac{mb^3 - n^2b - 2kn^2}{b^3} \end{align*} \]

导数求解最值取 \(f^{\prime}(b) = 0\)，则：

\[b={\left(\frac{ n^2\,\sqrt{-\frac{n^2-27\,k^2\,m}{m}}}{3^{\frac{3}{2}}\,m}+\frac{2\, n^2\,k}{2\,m}\right)}^{\frac{1}{3}}+\frac{n^2}{3\,m\,{\left(\frac{n^ 2\,\sqrt{-\frac{n^2-27\,k^2\,m}{m}}}{3^{\frac{3}{2}}\,m}+\frac{2\,n^ 2\,k}{2\,m}\right)}^{\frac{1}{3}}} \]

算了还是不往下算了。

如果非要卡常用这个 \(b\) 也不是不行。
我们观察到 \(b\) 的第一项其实在第二项中重复出现了，可以减少部分计算量。
即：

\[t = {\left(\frac{ n^2\,\sqrt{-\frac{n^2-27\,k^2\,m}{m}}}{3^{\frac{3}{2}}\,m}+\frac{2\, n^2\,k}{2\,m}\right)}^{\frac{1}{3}} \]

而：

\[b = t+\frac{n^2}{3mt} \]

当 \(b\) 取 \(n^{\frac{2}{3}}\) 时时间比较优秀，取 \(\mathcal O(n^{\frac{5}{3}})\)。

代码

这里也只放核心的代码：

int l = 1, r = 0, t = 0;
for (int i = 1; i <= cnt_q; i++) {
	while (l > q[i].l) add(a[--l]);
	while (r < q[i].r) add(a[++r]);
	while (l < q[i].l) del(a[l++]);
	while (r > q[i].r) del(a[r--]);
	while (t < q[i].t) upt(++t, i); // 更新修改
	while (t > q[i].t) upt(t--, i); 
	ans[q[i].id] = res;
}

upt 函数：

void upt(int x, int y) { // 单点赋值，区间赋值可以考虑差分
	if (q[y].l <= c[x].l && c[x].l <= q[y].r) {
		del(a[c[x].l]);
		add(c[x].r);
	}
	swap(a[c[x].l], c[x].r);
}

同样的，排序规则函数读者自证不难。

回滚莫队

由于部分题目增加数与减少数的复杂度不同，而慢的一个往往又无法接受，就出现了回滚莫队。

回滚莫队的本质是让插入（或删除）操作变少。

原理

这里先讲不删除莫队，不插入莫队原理大致相同。

将所有左端点块的编号相同的询问放到一个组里，我们发现，每个组中的 \(r\) 都是递增的（可参考普通莫队的排序方式）。

那么可以将 \(l\) 初值设为 \(l\) 所在块的右端点 \(+1\)（避免算漏），\(r\) 的初值设为块的右端点，像这样：

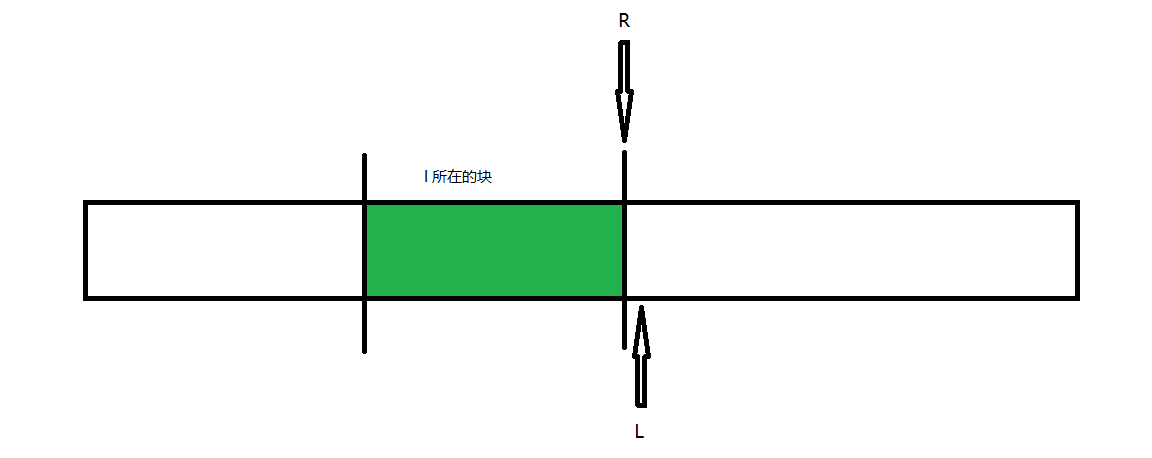
先将 \(r\) 指针挪到正确的右端点。

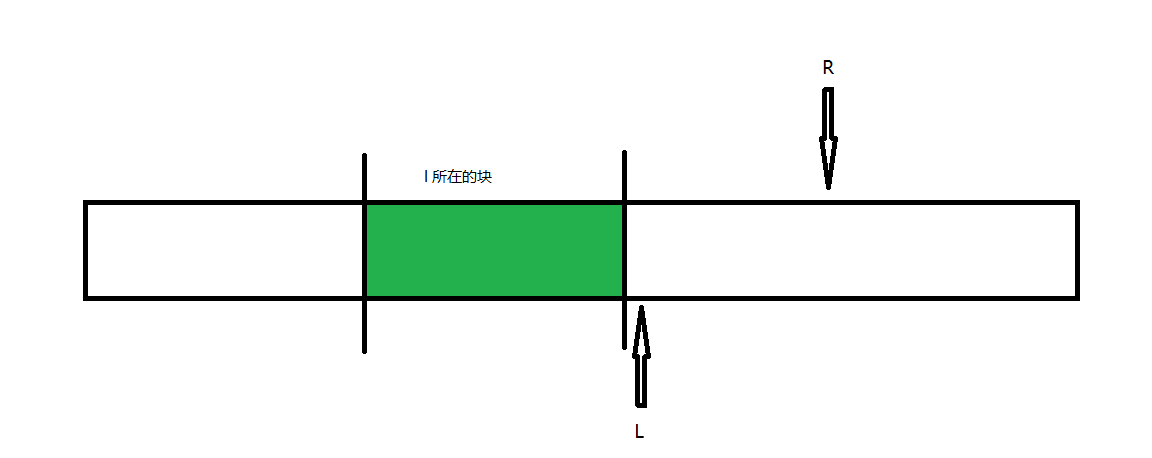
然后再把 \(l\) 挪到左端点。

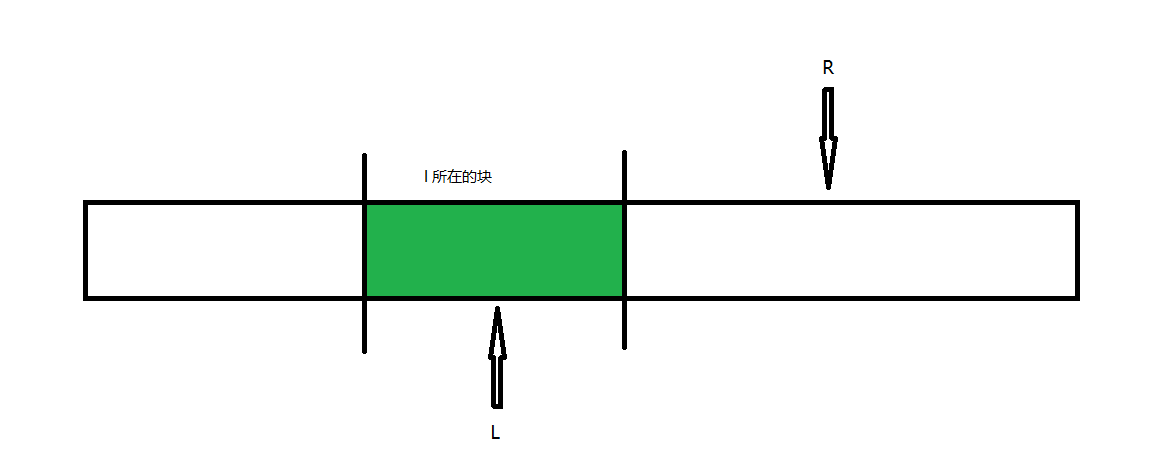
此时保存结果到结果数组中。

然后再滚回到原来的状态：

重复以上操作。

值得注意的一点是 \(r\) 指针并不需要回滚，因为在一组询问中，\(r\) 具有单调性，回滚了反而会增加时间。

按照逻辑写出核心代码即可。

代码

int l = 1, r = 0, qid = 1;
for (int i = 1; i <= bl[n]; i++) {
	// 清空 
	int R = min(n, i * block_size);
	l = R + 1, r = R; // 赋初值 
	ret = res = 0;
	for (; bl[q[qid].l] == i; qid++) {
		if (bl[q[qid].l] == bl[q[qid].r]) { // 在同一个块里就干脆暴力 
			// 暴力计算 
			continue;
		}
		while (r < q[qid].r) addr(++r);
		while (l > q[qid].l) addl(--l);
		ans[q[qid].id] = res;
		for (int j = l; j <= R + 1; j++) {
			// 回滚 
		}
		res = ret;
		l = R + 1;
	}
}