1496. 判断路径是否相交
1496. 判断路径是否相交
给你一个字符串 path,其中 path[i] 的值可以是 'N'、'S'、'E' 或者 'W',分别表示向北、向南、向东、向西移动一个单位。
机器人从二维平面上的原点 (0, 0) 处开始出发,按 path 所指示的路径行走。
如果路径在任何位置上出现相交的情况,也就是走到之前已经走过的位置,请返回 True ;否则,返回 False 。
示例 1:
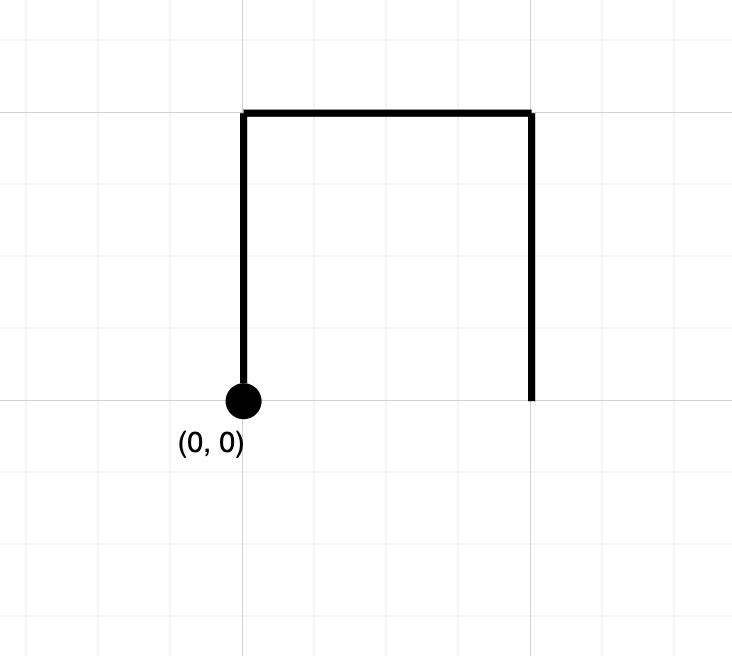
输入:path = "NES" 输出:false 解释:该路径没有在任何位置相交。
示例 2:
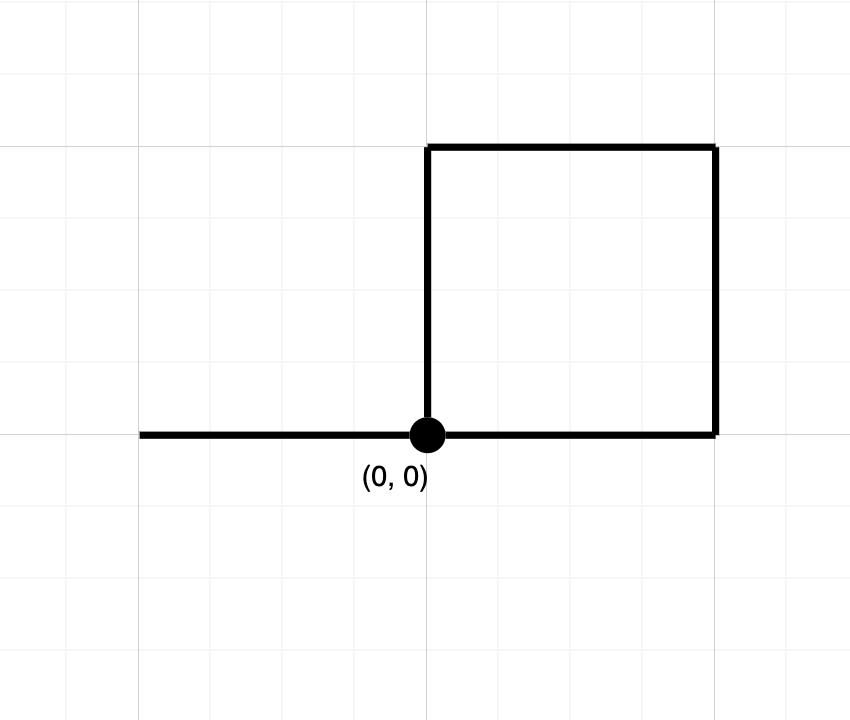
输入:path = "NESWW" 输出:true 解释:该路径经过原点两次。
提示:
1 <= path.length <= 10^4path仅由{'N', 'S', 'E', 'W}中的字符组成
给你一个字符串 path,其中 path[i] 的值可以是 'N'、'S'、'E' 或者 'W',分别表示向北、向南、向东、向西移动一个单位。
机器人从二维平面上的原点 (0, 0) 处开始出发,按 path 所指示的路径行走。
如果路径在任何位置上出现相交的情况,也就是走到之前已经走过的位置,请返回 True ;否则,返回 False 。
示例 1:

输入:path = "NES" 输出:false 解释:该路径没有在任何位置相交。
示例 2:

输入:path = "NESWW" 输出:true 解释:该路径经过原点两次。
提示:
1 <= path.length <= 10^4path仅由{'N', 'S', 'E', 'W}中的字符组成判断路径是否相交
力扣官方题解发布于 2020-07-012.8k官方C++JavaPython哈希表方法一:哈希表
思路
我们可以模拟机器人行走的过程,机器人行走的本质是它的坐标发生了变化,要解决这个问题,就要保存机器人走过的所有坐标——所以这道题的关键在于如何判断「走到之前已经走过的位置」。
由于数组 \it pathpath 的长度最大是 10^4104,我们并不能开一个二维数组来表示这个坐标平面:在极端情况下,机器人每次都沿着同一个方向前进,开二维数组需要 (10^4)^2(104)2 个布尔类型变量的空间,它非常大。实际上,这 (10^4)^2(104)2 个位置并不是都能用到,大多数位置是没有访问到的,用这样的方法打访问标记会造成很大的空间浪费。
因此我们可以用哈希表来解决这个问题,即我们可以给「已经走过」的位置打上访问标记,把坐标 (x, y)(x,y) 存入哈希表,每次模拟坐标的变化得到新的坐标,在哈希表中查询这个坐标对应的哈希值有没有出现过,这样既不用花费很大的空间,又能快速查询到一个坐标是否访问过。
在
C++语言中,如果使用pair<int, int>存储坐标,那么我们需要自己实现哈希映射函数。我们可以令哈希函数 f(x, y) = x \times 20001 + yf(x,y)=x×20001+y,这是因为 yy 的取值范围在 [-10^4, 10^4][−104,104] 内,共有 2000120001 种可能性,上述的哈希函数就不会造成冲突。在Python语言中,我们使用元组tuple存储坐标,可以直接放入哈希表set中。代码如下。
代码
![]()




 浙公网安备 33010602011771号
浙公网安备 33010602011771号