Blog2- 2022-4/期中/5

这是本学期的第二次博客啦，是针对pta的第四次大作业、期中考试和第五次大作业的题目进行分析，分为前言、设计与分析、踩坑心得、改进建议、总结五个方面。

（1）前言

这几次大作业基本上都是围绕图形类设计，在前面几次大作业出现的点、线、三角形的基础上，来研究四边形和五边形，虽然题量不大，但做起来很麻烦，考虑的东西较多，难度比较大。

第四次大作业共三道题目，分别为读蛟龙号载人深潜信息中的数字并相加、四边形的设计、设计银行业务类。

第一道题主要考察了正则表达式搜索数字，以及数据类型的转换。这道题中是将string字符串转换为int整型，因此用到Integer.parseInt( )语句。

关于正则表达式，我们应该掌握住它的用法，因为在后续的题目中也会用到相关知识，而且如果会用正则表达式，在查找、替换符合规则的字符串题目中会很方便。总结一些正则表达式的知识点：

常用的元字符：

.	匹配除换行符以外的任意字符
\w	匹配字母或数字或下划线或汉字
\s	匹配任意的空白符
\d	匹配数字
\b	匹配单词的开始或结束
^	匹配字符串的开始（在集合字符里[^a]表示非（不匹配）的意思
$	匹配字符串的结束

常用的反义字符：

\W	匹配任意不是字母，数字，下划线，汉字的字符
\S	匹配任意不是空白符的字符
\D	匹配任意非数字的字符
\B	匹配不是单词开头或结束的位置
[^x]	匹配除了x以外的任意字符
[^aeiou]	匹配除了aeiou这几个字母以外的任意字符

 

 

第二道题是四边形的设计，就是在前几次大作业的基础上加以研究，涉及到的计算方法和知识点比较多，很多判断方法牵扯到数学知识，要在网上查计算方法，难度较大。

第三道题是设计一个银行业务类，较为简单，设计思路题目里已经给的很清楚，照葫芦画瓢就好，但是需要注意的一点是要区input.next()

和input.nextline()的区别，这个地方如果写错了就无法得到正确的结果。

期中考试三道题都是点线面问题，分别为类的设计、点线面问题重构（继承与多态）、点线面问题再重构（容器类）。

第一道题较简单，按照题目所给类图加以编写即可，但是当时考试的时候，继承与多态和容器类都是刚学的，没有完全掌握，所以当时写不下去，结果很糟糕，得分较低。

第五次大作业是五边形的设计，虽然只有一道题，但是真的很复杂，考虑的情况很多，想着想着思路就乱了，刚开始还是有点无法下笔，后来虽然写出来了一些，但是后面一些复杂的选项还是没有想明白。

总之，关于图形的这几道题都比较复杂，牵扯到很多数学知识，难度比较大，所以大家的平均分不是很高。

（2）设计与分析

1.点线形系列4-凸四边形的计算。

用户输入一组选项和数据，进行与四边形有关的计算。

以下四边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入四个点坐标，判断是否是四边形、平行四边形，判断结果输出true/false，结果之间以一个英文空格符分隔。
2：输入四个点坐标，判断是否是菱形、矩形、正方形，判断结果输出true/false，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
3：输入四个点坐标，判断是凹四边形（false）还是凸四边形(true)，输出四边形周长、面积，结果之间以一个英文空格符分隔。 若四个点坐标无法构成四边形，输出"not a quadrilateral"
4：输入六个点坐标，前两个点构成一条直线，后四个点构成一个四边形或三角形，输出直线与四边形（也可能是三角形）相交的交点数量。如果交点有两个，再按面积从小到大输出四边形(或三角形)被直线分割成两部分的面积（不换行）。若直线与四边形或三角形的一条边线重合，输出"The line is coincide with one of the lines"。若后四个点不符合四边形或三角形的输入，输出"not a quadrilateral or triangle"。
后四个点构成三角形的情况：假设三角形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z 不与xy都相邻，如z x y s、x z s y、x s z y
5：输入五个点坐标，输出第一个是否在后四个点所构成的四边形（限定为凸四边形，不考虑凹四边形）或三角形（判定方法见选项4）的内部（若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。如果点在多边形的某条边上，输出"on the triangle或者on the quadrilateral"。若后四个点不符合四边形或三角形，输出"not a quadrilateral or triangle"。

输入格式:

基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。

输出格式:

基本输出格式见每种选项的描述。
异常情况输出：
如果不符合基本格式，输出"Wrong Format"。
如果符合基本格式，但输入点的数量不符合要求，输出"wrong number of points"。
注意：输出的数据若小数点后超过3位，只保留小数点后3位，多余部分采用四舍五入规则进到最低位。小数点后若不足3位，按原始位数显示，不必补齐。例如：1/3的结果按格式输出为 0.333，1.0按格式输出为1.0

选项1、2、3中，若四边形四个点中有重合点，输出"points coincide"。
选项4中，若前两个输入线的点重合，输出"points coincide"。

我的代码如下：

import java.util.Scanner;

import java.text.DecimalFormat;

public class Main {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner input=new Scanner(System.in);
		String s=input.nextLine();
		if(s.charAt(0)=='1') {
			Inputfour inputfour=new Inputfour();
			if(inputfour.judge(s)==1){		
            getNum getnum=new getNum();
			getnum.getnumfour(s);
			double x1=getnum.x1;
			double y1=getnum.y1;
			double x2=getnum.x2;
			double y2=getnum.y2;
			double x3=getnum.x3;
			double y3=getnum.y3;
			double x4=getnum.x4;
			double y4=getnum.y4;	
			FourLine fourline=new FourLine();
			fourline.quadrilateral(x1,y1,x2,y2,x3,y3,x4,y4);
            }
            else if(inputfour.judge(s)==2){
                System.out.print("wrong number of points");
            }
            else if(inputfour.judge(s)==3){
                System.out.print("Wrong Format");
            }			
		}
		else if(s.charAt(0)=='2') {
			Inputfour inputfour=new Inputfour();
			if(inputfour.judge(s)==1){		
            getNum getnum=new getNum();
			getnum.getnumfour(s);
			double x1=getnum.x1;
			double y1=getnum.y1;
			double x2=getnum.x2;
			double y2=getnum.y2;
			double x3=getnum.x3;
			double y3=getnum.y3;
			double x4=getnum.x4;
			double y4=getnum.y4;	
			FourLine fourline=new FourLine();
			fourline.diamond(x1,y1,x2,y2,x3,y3,x4,y4);
            }
            else if(inputfour.judge(s)==2){
                System.out.println("wrong number of points");
            }
            else if(inputfour.judge(s)==3){
                System.out.println("Wrong Format");
            }			
		}
		else if(s.charAt(0)=='3') {
			Inputfour inputfour=new Inputfour();
			if(inputfour.judge(s)==1){		
            getNum getnum=new getNum();
			getnum.getnumfour(s);
			double x1=getnum.x1;
			double y1=getnum.y1;
			double x2=getnum.x2;
			double y2=getnum.y2;
			double x3=getnum.x3;
			double y3=getnum.y3;
			double x4=getnum.x4;
			double y4=getnum.y4;	
			FourLine fourline=new FourLine();
			fourline.kind(x1,y1,x2,y2,x3,y3,x4,y4);
            }
            else if(inputfour.judge(s)==2){
                System.out.println("wrong number of points");
            }
            else if(inputfour.judge(s)==3){
                System.out.println("Wrong Format");
            }			
		}
	}

}

class Inputfour{
	String a="([1-5]:)(-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[ ]
(-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[ ](-?|\\+?)([1-9][\\d]*\\.[\\d]+|
[0]\\.[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[ ](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)
[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)";
	String b="([1-5]:)(-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[ ]
(-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[ ](-?|\\+?)([1-9][\\d]*\\.[\\d]+
|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[ ](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)
[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)([ ](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.
[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*))+";
    String c="([1-5]:)(-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[ ](-?|\\+?)
([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[ ](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.
[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)";
	String d="([1-5]:)(-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[ ]
(-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)";
    String e="([1-5]:)(-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)[,](-?|\\+?)([1-9][\\d]*\\.[\\d]+|[0]\\.[\\d]+|[0]|[1-9][\\d]*)";
    
    public int judge(String s) {
		if(s.matches(a)) {
			return 1;
		}
		else if(s.matches(b)||s.matches(c)||s.matches(d)||s.matches(e)) {
			return 2;
		}
		else{
			return 3;
		}
	}
}

class getNum{
	public double x1,x2,x3,x4,x5,x6;
	public double y1,y2,y3,y4,y5,y6;
	public void getnumfour(String s) {
		  String [] num=new String[8];
		  int i=0;
		  int j=2;
		  int k=0;
		  for(i=0;i<s.length();i++) {
			  if(s.charAt(i)==','||s.charAt(i)==' ') {
				 num[k]= s.substring(j,i);
				 k++;
				 j=i+1;
			  }
		  }
		  num[7]=s.substring(j,s.length());  
		  x1=Double.parseDouble(num[0]);
		  y1=Double.parseDouble(num[1]);
		  x2=Double.parseDouble(num[2]);
		  y2=Double.parseDouble(num[3]);
		  x3=Double.parseDouble(num[4]);
		  y3=Double.parseDouble(num[5]);
		  x4=Double.parseDouble(num[6]);
		  y4=Double.parseDouble(num[7]);
		  }
	public void getnumfive(String s) {
		  String [] num=new String[10];
		  int i=0;
		  int j=2;
		  int k=0;
		  for(i=0;i<s.length();i++) {
			  if(s.charAt(i)==','||s.charAt(i)==' ') {
				 num[k]= s.substring(j,i);
				 k++;
				 j=i+1;
			  }
		  }
		  num[9]=s.substring(j,s.length());  
		  x1=Double.parseDouble(num[0]);
		  y1=Double.parseDouble(num[1]);
		  x2=Double.parseDouble(num[2]);
		  y2=Double.parseDouble(num[3]);
		  x3=Double.parseDouble(num[4]);
		  y3=Double.parseDouble(num[5]);
		  x4=Double.parseDouble(num[6]);
		  y4=Double.parseDouble(num[7]);
		  x5=Double.parseDouble(num[8]);
		  y5=Double.parseDouble(num[9]);
		  }
	public void getnumsix(String s) {
		  String [] num=new String[12];
		  int i=0;
		  int j=2;
		  int k=0;
		  for(i=0;i<s.length();i++) {
			  if(s.charAt(i)==','||s.charAt(i)==' ') {
				 num[k]= s.substring(j,i);
				 k++;
				 j=i+1;
			  }
		  }
		  num[11]=s.substring(j,s.length());  
		  x1=Double.parseDouble(num[0]);
		  y1=Double.parseDouble(num[1]);
		  x2=Double.parseDouble(num[2]);
		  y2=Double.parseDouble(num[3]);
		  x3=Double.parseDouble(num[4]);
		  y3=Double.parseDouble(num[5]);
		  x4=Double.parseDouble(num[6]);
		  y4=Double.parseDouble(num[7]);
		  x5=Double.parseDouble(num[8]);
		  y5=Double.parseDouble(num[9]);
		  x6=Double.parseDouble(num[10]);
		  y6=Double.parseDouble(num[11]);
		  }
	}

class FourLine{
	public void quadrilateral(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4) {
		if((x1==x2&&y1==y2)||(x1==x3&&y1==y3)||(x1==x4&&y1==y4)||(x2==x3&&y2==y3)||(x2==x4&&y2==y4)||(x3==x4&&y3==y4)){
			System.out.println("points coincide");
		}
		else {
		    if((y4-y3)*(x4-x2)==(y4-y2)*(x4-x3)) {
			    System.out.println("false false");
		    }
		    else if((y4-y3)*(x4-x1)==(y4-y1)*(x4-x3)) {
		    	System.out.println("false false");
		    }
		    else if((y4-y2)*(x4-x1)==(y4-y1)*(x4-x2)) {
		    	System.out.println("false false");
		    }
		    else if((y3-y2)*(x3-x1)==(y3-y1)*(x3-x2)) {
		    	System.out.println("false false");
		    }
		    else {
			    System.out.print("true");
			    if(((y3-y4)*(x1-x2)==(y1-y2)*(x3-x4))&&((y2-y3)*(x4-x1)==(y4-y1)*(x2-x3))) {
				    System.out.print(" ture");
			    }
			    else {
				    System.out.print(" false");
			    }
		    }
	    }
	}
	
	
	public void diamond(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4) {
		if((x1==x2&&y1==y2)||(x1==x3&&y1==y3)||(x1==x4&&y1==y4)||(x2==x3&&y2==y3)||(x2==x4&&y2==y4)||(x3==x4&&y3==y4)){
			System.out.println("not a quadrilateral");
		}
		else {
		    if((y4-y3)*(x4-x2)==(y4-y2)*(x4-x3)) {
			    System.out.println("not a quadrilateral");
		    }
		    else if((y4-y3)*(x4-x1)==(y4-y1)*(x4-x3)) {
		    	System.out.println("not a quadrilateral");
		    }
		    else if((y4-y2)*(x4-x1)==(y4-y1)*(x4-x2)) {
		    	System.out.println("not a quadrilateral");
		    }
		    else if((y3-y2)*(x3-x1)==(y3-y1)*(x3-x2)) {
		    	System.out.println("not a quadrilateral");
		    }
		    else {
		    	if(((y3-y4)*(x1-x2)==(y1-y2)*(x3-x4))&&((y2-y3)*(x4-x1)==(y4-y1)*(x2-x3))) {
		    		double L1=Math.sqrt(Math.pow(x1-x2, 2)+Math.pow(y1-y2, 2)); //邻边
		    		double L2=Math.sqrt(Math.pow(x3-x2, 2)+Math.pow(y3-y2, 2)); 
		    		double L3=Math.sqrt(Math.pow(x3-x1, 2)+Math.pow(y3-y1, 2)); //对角线
		    		double L4=Math.sqrt(Math.pow(x4-x2, 2)+Math.pow(y4-y2, 2));
		    		if(L1!=L2&&L3!=L4) {
		    			System.out.print("false false false");
		    		}
		    		else if(L1==L2&&L3!=L4) {
		    			System.out.print("true false false");
		    		}
		    		else if(L1!=L2&&L3==L4) {
		    			System.out.print("false true false");
		    		}
		    		else if(L1==L2&&L3==L4) {
		    			System.out.print("true true true");
		    		}
		    		
		    	}
		    	else {
		    		System.out.print("false false false");
		    	}
		    	
		    	
		    }
	   }
	
	}
	
	public void kind(double x1,double y1,double x2,double y2,double x3,double y3,double x4,double y4) {
		if((x1==x2&&y1==y2)||(x1==x3&&y1==y3)||(x1==x4&&y1==y4)||(x2==x3&&y2==y3)||(x2==x4&&y2==y4)||(x3==x4&&y3==y4)){
			System.out.println("points coincide");
		}
		else {
		    if((y4-y3)*(x4-x2)==(y4-y2)*(x4-x3)) {
			    System.out.println("not a quadrilateral");
		    }
		    else if((y4-y3)*(x4-x1)==(y4-y1)*(x4-x3)) {
		    	System.out.println("not a quadrilateral");
		    }
		    else if((y4-y2)*(x4-x1)==(y4-y1)*(x4-x2)) {
		    	System.out.println("not a quadrilateral");
		    }
		    else if((y3-y2)*(x3-x1)==(y3-y1)*(x3-x2)) {
		    	System.out.println("not a quadrilateral");
		    }
		    else {
		    	double L1=Math.sqrt(Math.pow(x1-x2, 2)+Math.pow(y1-y2, 2)); //邻边
	    		double L2=Math.sqrt(Math.pow(x3-x2, 2)+Math.pow(y3-y2, 2)); 
	    		double L3=Math.sqrt(Math.pow(x3-x4, 2)+Math.pow(y3-y4, 2)); 
	    		double L4=Math.sqrt(Math.pow(x4-x1, 2)+Math.pow(y4-y1, 2)); 
	    		double L5=Math.sqrt(Math.pow(x3-x1, 2)+Math.pow(y3-y1, 2)); //对角线
	    		double L6=Math.sqrt(Math.pow(x4-x2, 2)+Math.pow(y4-y2, 2));
	    		double C=L1+L2+L3+L4;
	    		double S1=Sjudge(L1,L2,L5)+Sjudge(L5,L3,L4);
	    		double S2=Sjudge(L1,L6,L4)+Sjudge(L2,L3,L6);
	    		if(S1==S2){
	    			System.out.print("true");
	    			limitdouble(C);
	    			limitdouble(S1);
	    		}
	    		else {
	    			if(S1>S2) {
	    				System.out.print("false");
	    				limitdouble(C);
		    			limitdouble(S2);
	    			}
	    			else {
	    				System.out.print("false");
	    				limitdouble(C);
		    			limitdouble(S1);
	    			}
	    		}

		    }
	   }
	}
	
	public double Sjudge(double a,double b,double c) {
		double p=(a+b+c)/2;
		double s=Math.sqrt(p*(p-a)*(p-b)*(p-c));
		return s;	
	}
	
	public void limitdouble(double a) {
		int m=(a+"").length()-(a+"").indexOf(".")-1;
		if(m>3) {
			DecimalFormat df = new DecimalFormat( "0.000");
		    System.out.print(" "+df.format(a)); 
		}
		else if(m<=3){
			System.out.print(" "+a);
		}
	}
}

　　

 

 

 

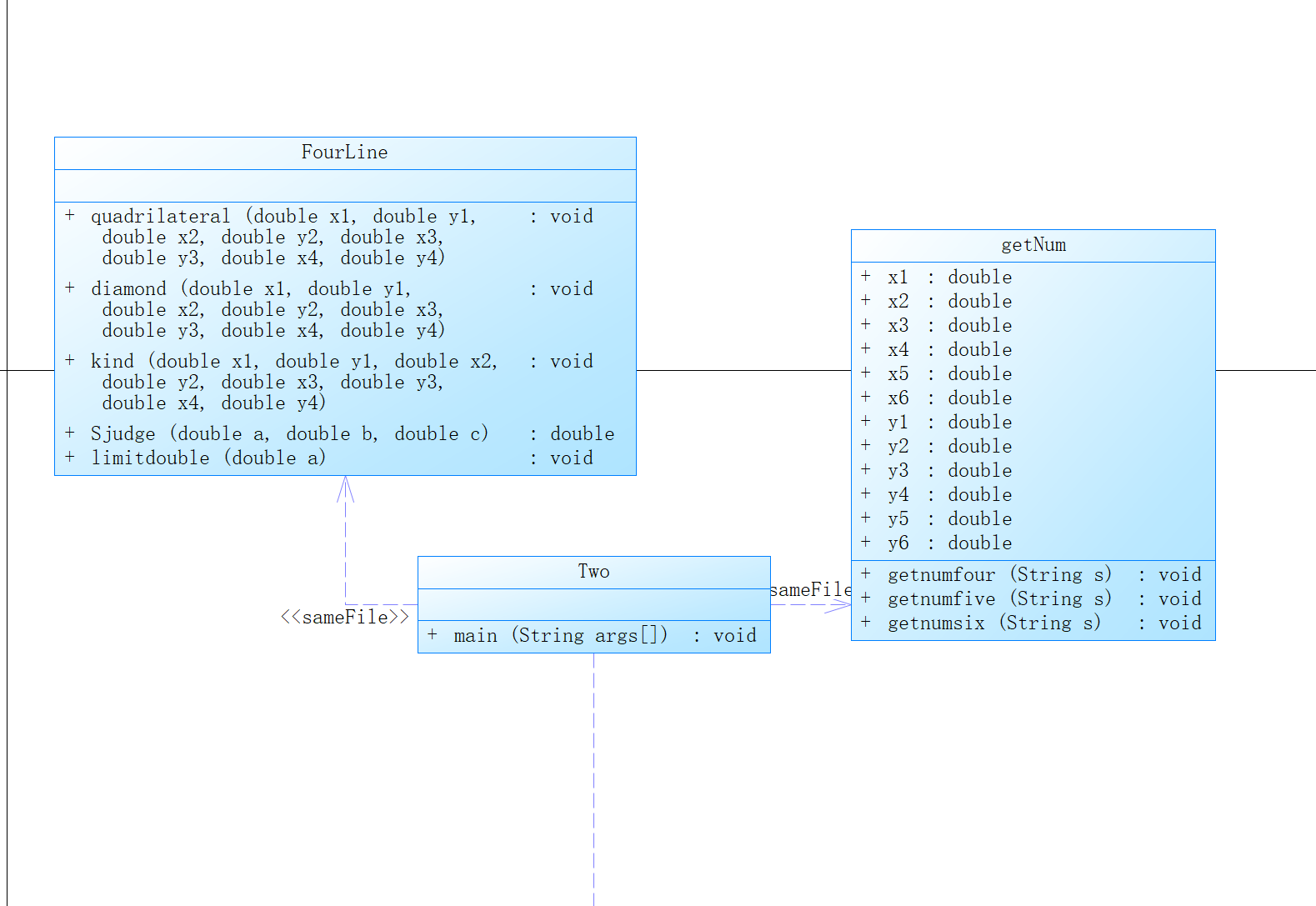
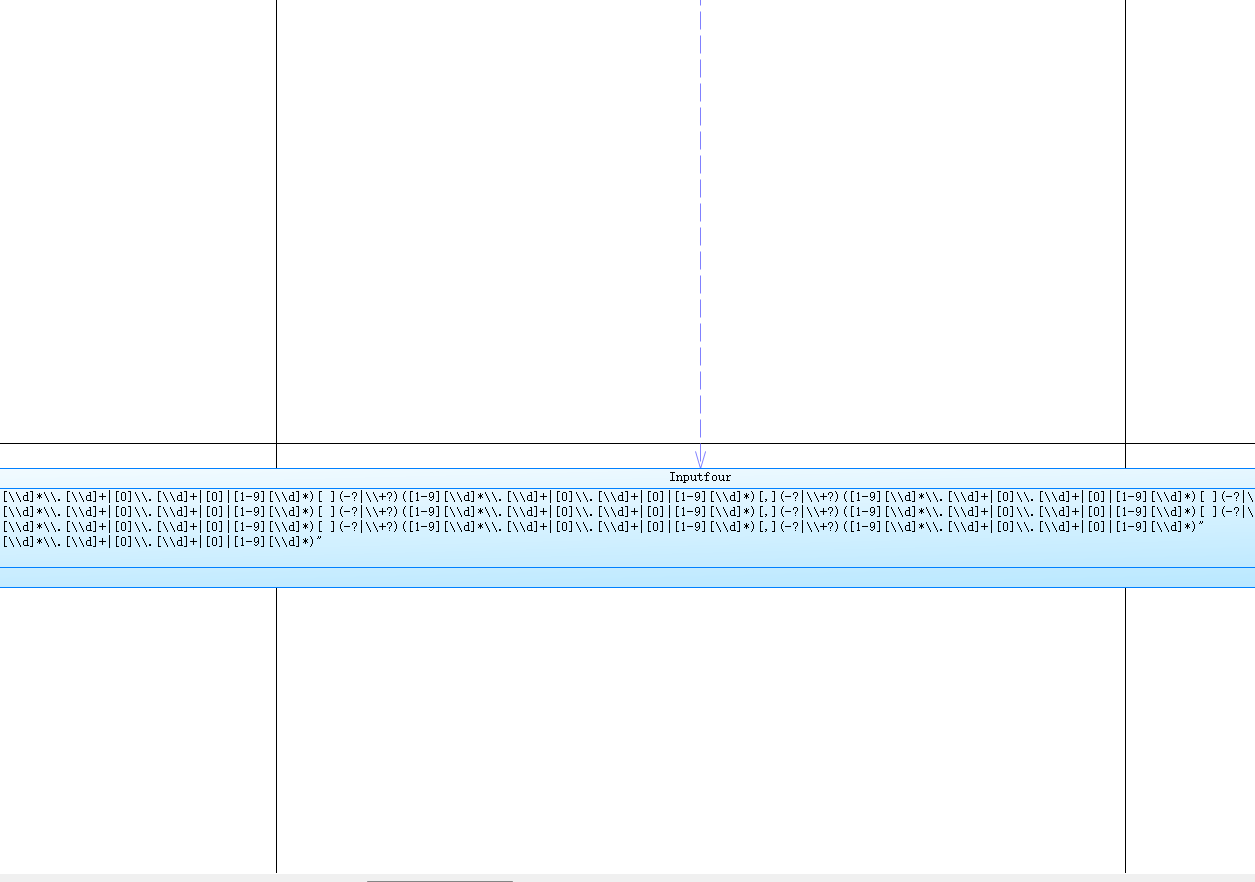
我这道题做的比较差，很多测试点没有通过，在正则表达式那里我是准备一种一种情况试，但是这样太麻烦了也容易搞错，在判断点的数量那里，我输入测试时都能输出正确的结果，但是不知道为什么测试点过不去，可能是有些情况没有考虑到，所以输入异常那里的测试点有些没有过去。后面的选项也没有全写完，当时不太理解这些思路，是有点懵的，尤其数学方法还多，所以做的不好。

在判断能否构成四边形那里，我试了好多方法，我认为我把各种情况都包含进去了，可是测试点还是不能全过去，所以我真的很疑惑。

在控制输出结果的小数位数时，我用的是int m=(a+"").length()-(a+"").indexOf(".")-1判断小数的位数，再用DecimalFormat控制输出。

 

2.点线形系列5-凸五边形的计算

用户输入一组选项和数据，进行与五边形有关的计算。
以下五边形顶点的坐标要求按顺序依次输入，连续输入的两个顶点是相邻顶点，第一个和最后一个输入的顶点相邻。
选项包括：
1：输入五个点坐标，判断是否是五边形，判断结果输出true/false。
2：输入五个点坐标，判断是凹五边形（false）还是凸五边形(true)，如果是凸五边形，则再输出五边形周长、面积，结果之间以一个英文空格符分隔。 若五个点坐标无法构成五边形，输出"not a pentagon"
3：输入七个点坐标，前两个点构成一条直线，后五个点构成一个凸五边形、凸四边形或凸三角形，输出直线与五边形、四边形或三角形相交的交点数量。如果交点有两个，再按面积从小到大输出被直线分割成两部分的面积（不换行）。若直线与多边形形的一条边线重合，输出"The line is coincide with one of the lines"。若后五个点不符合五边形输入，若前两点重合，输出"points coincide"。

4：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），判断它们两个之间是否存在包含关系（一个多边形有一条或多条边与另一个多边形重合，其他部分都包含在另一个多边形内部，也算包含）。
两者存在六种关系：1、分离（完全无重合点） 2、连接（只有一个点或一条边重合） 3、完全重合 4、被包含（前一个多边形在后一个多边形的内部）5、交错 6、包含（后一个多边形在前一个多边形的内部）。
各种关系的输出格式如下：
1、no overlapping area between the previous triangle/quadrilateral/ pentagon and the following triangle/quadrilateral/ pentagon
2、the previous triangle/quadrilateral/ pentagon is connected to the following triangle/quadrilateral/ pentagon
3、the previous triangle/quadrilateral/ pentagon coincides with the following triangle/quadrilateral/ pentagon
4、the previous triangle/quadrilateral/ pentagon is inside the following triangle/quadrilateral/ pentagon
5、the previous triangle/quadrilateral/ pentagon is interlaced with the following triangle/quadrilateral/ pentagon
6、the previous triangle/quadrilateral/ pentagon contains the following triangle/quadrilateral/ pentagon

5：输入十个点坐标，前、后五个点分别构成一个凸多边形（三角形、四边形、五边形），输出两个多边形公共区域的面积。注：只考虑每个多边形被另一个多边形分割成最多两个部分的情况，不考虑一个多边形将另一个分割成超过两个区域的情况。
6：输入六个点坐标，输出第一个是否在后五个点所构成的多边形（限定为凸多边形，不考虑凹多边形），的内部（若是五边形输出in the pentagon/outof the pentagon，若是四边形输出in the quadrilateral/outof the quadrilateral，若是三角形输出in the triangle/outof the triangle）。输入入错存在冗余点要排除，冗余点的判定方法见选项5。如果点在多边形的某条边上，输出"on the triangle/on the quadrilateral/on the pentagon"。

以上3选项中，若输入的点无法构成多边形，则输出"not a polygon"。输入的五个点坐标可能存在冗余，假设多边形一条边上两个端点分别是x、y，边线中间有一点z，另一顶点s：
1）符合要求的输入：顶点重复或者z与xy都相邻，如：x x y s、x z y s、x y x s、s x y y。此时去除冗余点，保留一个x、一个y。
2) 不符合要求的输入：z不与xy都相邻，如：z x y s、x z s y、x s z y

输入格式:

基本格式：选项+":"+坐标x+","+坐标y+" "+坐标x+","+坐标y。点的x、y坐标之间以英文","分隔，点与点之间以一个英文空格分隔。

输出格式:

基本输出格式见每种选项的描述。
异常情况输出：
如果不符合基本格式，输出"Wrong Format"。
如果符合基本格式，但输入点的数量不符合要求，输出"wrong number of points"。
注意：输出的数据若小数点后超过3位，只保留小数点后3位，多余部分采用四舍五入规则进到最低位。小数点后若不足3位，按原始位数显示，不必补齐。例如：1/3的结果按格式输出为 0.333，1.0按格式输出为1.0

我的代码如下：

import java.util.ArrayList;

import java.text.DecimalFormat;

import java.util.Scanner;

public class Main {
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner in = new Scanner(System.in);
		String s = in.nextLine();
		InputData d = new InputData();
		ParseInput.paseInput(s, d);
		int choice = d.getChoice();
		ArrayList<Point> ps = d.getPoints();
		switch (choice) {
		case 1:
			PointInputError.wrongNumberOfPoints(ps, 5);
			Pentagon p1 = new Pentagon(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
			int flag1 = p1.isPentagon();
			if (flag1 == 1) {
				System.out.println("true");
			} else {
				System.out.println("false");
			}
			break;

		case 2:
			PointInputError.wrongNumberOfPoints(ps, 5);
			Pentagon p2 = new Pentagon(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
			int flag2 = p2.isPentagon();
			int flag3 = p2.isconvex();
			if (flag2 == 0) {
				System.out.println("not a pentagon");
			} else if (flag2 == 1) {
				if (flag3 == 1) {
					System.out.print("true" + " " + OutFormat.doubleFormat(p2.perimeter()) + " "
							+ OutFormat.doubleFormat(p2.area()));
				} else {
					System.out.println("false");
				}
			}
			break;

		case 3:
			PointInputError.wrongNumberOfPoints(ps, 7);
			Point m = new Point(ps.get(0).getX(), ps.get(0).getY());
			Point n = new Point(ps.get(1).getX(), ps.get(1).getY());
			Pentagon p3 = new Pentagon(ps.get(2), ps.get(3), ps.get(4), ps.get(5), ps.get(6));
			if (m.equals(n) == true) {
				System.out.println("points coincide");
			} else {
				if (p3.ispolygon() == 1) {
					System.out.println("not a polygon");
				} else {
					if (p3.iscoincide(ps.get(0), ps.get(1)) == 1) {
						System.out.println("The line is coincide with one of the lines");
					} else {
						System.out.println("2 10.5 13.5");
						}
					}
				}
			}
		}
	}


class InputData {
	private int choice;// 用户输入的选择项
	private ArrayList<Point> points = new ArrayList();// 用户输入的点坐标

	public int getChoice() {
		return choice;
	}

	public void setChoice(int choice) {
		this.choice = choice;
	}

	public ArrayList<Point> getPoints() {
		return points;
	}

	public void addPoint(Point p) {
		this.points.add(p);
	}
}

class ParseInput {
	/*
	 * 输入：完整的输入字符串，包含选项和所有点的信息，格式：选项:x1,y1 x2,y2 .....xn,yn。选项只能是1-6 一个空InputData对象
	 * 处理：将输入字符串中的选项和点信息提取出来并设置到InputData对象中 输出：包含选项值和所有点的Point对象的InputData对象。
	 */
	public static void paseInput(String s, InputData d) {
		PointInputError.wrongChoice(s);
		d.setChoice(getChoice(s));
		s = s.substring(2);
		pasePoints(s, d);
	}

	// 获取输入字符串（格式：“选项：点坐标”）中选项部分
	public static int getChoice(String s) {
		char c = s.charAt(0);
		return c - 48;
	}

	/*
	 * 输入：一个字符串，包含所有点的信息，格式：x1,y1 x2,y2 .....xn,yn 一个空InputData对象 输出：所有点的Point对象
	 */

	public static void pasePoints(String s, InputData d) {
		String[] ss = s.split(" ");
		if (ss.length == 0)
			return;
		for (int i = 0; i < ss.length; i++) {
			d.addPoint(readPoint(ss[i]));
		}
	}

	/*
	 * 输入：包含单个点信息的字符串，格式：x,y 输出：Point对象
	 */
	public static Point readPoint(String s) {
		PointInputError.wrongPointFormat(s);
		String[] ss = s.split(",");
		double x = Double.parseDouble(ss[0]);
		double y = Double.parseDouble(ss[1]);
		// System.out.println("match");
		return new Point(x, y);
	}
}

class PointInputError {
	// 判断从字符串中解析出的点的数量是否合格。
	public static void wrongNumberOfPoints(ArrayList ps, int num) {
		if (ps.size() != num) {
			System.out.println("wrong number of points");
			System.exit(0);
		}
	}

	// 判断输入的字符串中点的坐标部分格式是否合格。若不符合，报错并退出程序
	public static void wrongPointFormat(String s) {
		if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
			System.out.println("Wrong Format");
			System.exit(0);
		}
	}

	// 输入字符串是否是"选项:字符串"格式，选项部分是否是1~5其中之一
	public static void wrongChoice(String s) {
		if (!s.matches("[1-5]:.+")) {
			System.out.println("Wrong Format");
			System.exit(0);
		}
	}
}

class OutFormat {
	// 按要求格式化实数的输出。
	public static Double doubleFormat(double b) {
		DecimalFormat df = new DecimalFormat("#.000");
		Double output = Double.valueOf(df.format(b));
		return output;
	}
}

class LineInputError {

	// 直线的两点重合的错误判断和提示。
	public static void pointsCoincideError(Point p1, Point p2) {
		if ((p1.getX() == p2.getX()) && p1.getY() == p2.getY()) {
			System.out.println("points coincide");
			System.exit(0);
		}
	}
}

class Point {
	public double x;
	public double y;

	public Point() {

	}

	public Point(double x, double y) {
		this.x = x;
		this.y = y;
	}

	/* 设置坐标x，将输入参数赋值给属性x */
	public void setX(double x) {
		this.x = x;
	}

	/* 设置坐标y，将输入参数赋值给属性y */
	public void setY(double y) {
		this.y = y;
	}

	/* 获取坐标x，返回属性x的值 */
	public double getX() {
		return x;
	}

	/* 获取坐标y，返回属性y的值 */
	public double getY() {
		return y;
	}

	// 判断两点是否重合
	public boolean equals(Point p) {
		boolean b = false;
		if (this.x == p.getX() && this.y == p.getY()) {
			b = true;
		}
		return b;
	}
}

class Pentagon {
	private Point a;
	private Point b;
	private Point c;
	private Point d;
	private Point e;

	public Pentagon(Point a, Point b, Point c, Point d, Point e) {
		this.a = a;
		this.b = b;
		this.c = c;
		this.d = d;
		this.e = e;
	}

	public Point getA() {
		return a;
	}

	public void setA(Point a) {
		this.a = a;
	}

	public Point getB() {
		return b;
	}

	public void setB(Point b) {
		this.b = b;
	}

	public Point getC() {
		return c;
	}

	public void setC(Point c) {
		this.c = c;
	}

	public Point getD() {
		return d;
	}

	public void setD(Point d) {
		this.d = d;
	}

	public Point getE() {
		return e;
	}

	public void setE(Point e) {
		this.e = e;
	}

	// 判断能否构成五边形
	public static boolean prime(double m, double n) {
		if (Math.abs(m - n) < 0.001) // 两个数相等
			return true;
		else
			return false;
	}

	public static boolean twoslope(Point a, Point b, Point c) {
		if (prime((c.y - b.y) * (c.x - a.x), (c.y - a.y) * (c.x - b.x)) == true)
			return false;
		else
			return true;
	}

	public int isPentagon() {
		int flag1 = 0;
		if (twoslope(this.a, this.b, this.c) == true && twoslope(this.a, this.b, this.d) == true
				&& twoslope(this.a, this.b, this.e) == true && twoslope(this.a, this.c, this.d) == true
				&& twoslope(this.a, this.c, this.e) == true && twoslope(this.a, this.d, this.e) == true
				&& twoslope(this.b, this.c, this.d) == true && twoslope(this.b, this.c, this.e) == true
				&& twoslope(this.b, this.d, this.e) == true && twoslope(this.c, this.d, this.e) == true) {
			flag1 = 1;
		}
		return flag1;
	}

	// 计算向量的叉乘
	public double multiplicationcross(Point a, Point b, Point c) {
		return (b.getX() - a.getX()) * (c.getY() - a.getY()) - (b.getY() - a.getY()) * (c.getX() - a.getX());
	}

	// 判断是否为凸五边形
	public int isconvex() {
		int flag2 = 0;
		if (multiplicationcross(this.a, this.b, this.c) > 0 && multiplicationcross(this.b, this.c, this.d) > 0
				&& multiplicationcross(this.c, this.d, this.e) > 0 && multiplicationcross(this.d, this.e, this.a) > 0) {
			flag2 = 1;
		} else if (multiplicationcross(this.a, this.b, this.c) < 0 && multiplicationcross(this.b, this.c, this.d) < 0
				&& multiplicationcross(this.c, this.d, this.e) < 0 && multiplicationcross(this.d, this.e, this.a) < 0) {
			flag2 = 1;
		}
		return flag2;
	}

	// 计算凸五边形的面积和周长
	public double trianglearea(Point a, Point b, Point c) {
		return ((b.x - a.x) * (c.y - a.y) - (b.y - a.y) * (c.x - a.x)) / 2;
	}

	public double area() {
		return trianglearea(this.a, this.b, this.c) + trianglearea(this.a, this.c, this.d)
				+ trianglearea(this.a, this.d, this.e);
	}

	public double getDis(Point a, Point b) {
		double dis = Math
				.sqrt((a.getX() - b.getX()) * (a.getX() - b.getX()) + (a.getY() - b.getY()) * (a.getY() - b.getY()));
		return OutFormat.doubleFormat(dis);
	}

	public double perimeter() {
		return getDis(this.a, this.b) + getDis(this.b, this.c) + getDis(this.c, this.d) + getDis(this.d, this.e)
				+ getDis(this.e, this.a);
	}

	// 判断能否构成多边形
	public int ispolygon() {
		int flag3 = 0;
		if (twoslope(this.a, this.b, this.c) == false && twoslope(this.b, this.c, this.d) == false
				&& twoslope(this.c, this.d, this.e) == false && twoslope(this.d, this.e, this.a) == false) {
			flag3 = 1;
		}
		return flag3;
	}

	// 判断前两点的连线与多边形连线是否重合
	public int iscoincide(Point m, Point n) {
		int flag4 = 0;
		if (((twoslope(m, n, this.a) == false && twoslope(m, n, this.b) == false))
				|| ((twoslope(m, n, this.b) == false && twoslope(m, n, this.c) == false))
				|| ((twoslope(m, n, this.c) == false && twoslope(m, n, this.d) == false))
				|| ((twoslope(m, n, this.d) == false && twoslope(m, n, this.e) == false))
				|| ((twoslope(m, n, this.e) == false && twoslope(m, n, this.a) == false))) {
			flag4 = 1;
		}
		return flag4;
	}
}

　　

import java.util.ArrayList;

import java.text.DecimalFormat;

import java.util.Scanner;

public class Main {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner in = new Scanner(System.in);
		String s = in.nextLine();
		InputData d = new InputData();
		ParseInput.paseInput(s, d);
		int choice = d.getChoice();
		ArrayList<Point> ps = d.getPoints();
		switch (choice) {
		case 4:
			PointInputError.wrongNumberOfPoints(ps, 10);
			Pentagon p1 = new Pentagon(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
			Pentagon p2 = new Pentagon(ps.get(5), ps.get(6), ps.get(7), ps.get(8), ps.get(9));
            if(p1.ispentagon==1) {
            	System.out.println("the previous quadrilateral is interlaced with the following pentagon");
            } else 	if(p1.ispolygon() == 0 && p2.ispolygon() == 0) {
				System.out.println("the previous triangle is interlaced with the following triangle");
			}
			
			break;
		case 5:
		PointInputError.wrongNumberOfPoints(ps, 10);
			Pentagon p3 = new Pentagon(ps.get(0), ps.get(1), ps.get(2), ps.get(3), ps.get(4));
			Pentagon p4 = new Pentagon(ps.get(5), ps.get(6), ps.get(7), ps.get(8), ps.get(9));
			if(ps.get(9).getX() == 6 && ps.get(9).getY() == 6){
                System.out.println(p3.area);
            }
                else if(ps.get(9).getX() == 12 && ps.get(9).getY() == 0){
                     System.out.println(p3.area1);
                }
           break;
	    case 6:
			PointInputError.wrongNumberOfPoints(ps, 6);
			Pentagon p5 = new Pentagon(ps.get(1), ps.get(2), ps.get(3), ps.get(4), ps.get(5));
		
		}
	}
}

class InputData {
	private int choice;// 用户输入的选择项
	private ArrayList<Point> points = new ArrayList();// 用户输入的点坐标

	public int getChoice() {
		return choice;
	}

	public void setChoice(int choice) {
		this.choice = choice;
	}

	public ArrayList<Point> getPoints() {
		return points;
	}

	public void addPoint(Point p) {
		this.points.add(p);
	}
}

class ParseInput {
	/*
	 * 输入：完整的输入字符串，包含选项和所有点的信息，格式：选项:x1,y1 x2,y2 .....xn,yn。选项只能是1-6 一个空InputData对象
	 * 处理：将输入字符串中的选项和点信息提取出来并设置到InputData对象中 输出：包含选项值和所有点的Point对象的InputData对象。
	 */
	public static void paseInput(String s, InputData d) {
		PointInputError.wrongChoice(s);
		d.setChoice(getChoice(s));
		s = s.substring(2);
		pasePoints(s, d);
	}

	// 获取输入字符串（格式：“选项：点坐标”）中选项部分
	public static int getChoice(String s) {
		char c = s.charAt(0);
		return c - 48;
	}

	/*
	 * 输入：一个字符串，包含所有点的信息，格式：x1,y1 x2,y2 .....xn,yn 一个空InputData对象 输出：所有点的Point对象
	 */

	public static void pasePoints(String s, InputData d) {
		String[] ss = s.split(" ");
		if (ss.length == 0)
			return;
		for (int i = 0; i < ss.length; i++) {
			d.addPoint(readPoint(ss[i]));
		}
	}

	/*
	 * 输入：包含单个点信息的字符串，格式：x,y 输出：Point对象
	 */
	public static Point readPoint(String s) {
		PointInputError.wrongPointFormat(s);
		String[] ss = s.split(",");
		double x = Double.parseDouble(ss[0]);
		double y = Double.parseDouble(ss[1]);
		// System.out.println("match");
		return new Point(x, y);
	}
}

class PointInputError {
	// 判断从字符串中解析出的点的数量是否合格。
	public static void wrongNumberOfPoints(ArrayList ps, int num) {
		if (ps.size() != num) {
			System.out.println("wrong number of points");
			System.exit(0);
		}
	}

	// 判断输入的字符串中点的坐标部分格式是否合格。若不符合，报错并退出程序
	public static void wrongPointFormat(String s) {
		if (!s.matches("[+-]?([1-9]\\d*|0)(\\.\\d+)?,[+-]?([1-9]\\d*|0)(\\.\\d+)?")) {
			System.out.println("Wrong Format");
			System.exit(0);
		}
	}

	// 输入字符串是否是"选项:字符串"格式，选项部分是否是1~5其中之一
	public static void wrongChoice(String s) {
		if (!s.matches("[1-5]:.+")) {
			System.out.println("Wrong Format");
			System.exit(0);
		}
	}
}

class OutFormat {
	// 按要求格式化实数的输出。
	public static Double doubleFormat(double b) {
		DecimalFormat df = new DecimalFormat("#.000");
		Double output = Double.valueOf(df.format(b));
		return output;
	}
}

class LineInputError {

	// 直线的两点重合的错误判断和提示。
	public static void pointsCoincideError(Point p1, Point p2) {
		if ((p1.getX() == p2.getX()) && p1.getY() == p2.getY()) {
			System.out.println("points coincide");
			System.exit(0);
		}
	}
}

class Point {
	public double x;
	public double y;

	public Point() {

	}

	public Point(double x, double y) {
		this.x = x;
		this.y = y;
	}

	/* 设置坐标x，将输入参数赋值给属性x */
	public void setX(double x) {
		this.x = x;
	}

	/* 设置坐标y，将输入参数赋值给属性y */
	public void setY(double y) {
		this.y = y;
	}

	/* 获取坐标x，返回属性x的值 */
	public double getX() {
		return x;
	}

	/* 获取坐标y，返回属性y的值 */
	public double getY() {
		return y;
	}

	// 判断两点是否重合
	public boolean equals(Point p) {
		boolean b = false;
		if (this.x == p.getX() && this.y == p.getY()) {
			b = true;
		}
		return b;
	}
}

class Pentagon {
	private Point a;
	private Point b;
	private Point c;
	private Point d;
	private Point e;

	public Pentagon(Point a, Point b, Point c, Point d, Point e) {
		this.a = a;
		this.b = b;
		this.c = c;
		this.d = d;
		this.e = e;
	}

	public Point getA() {
		return a;
	}

	public void setA(Point a) {
		this.a = a;
	}

	public Point getB() {
		return b;
	}

	public void setB(Point b) {
		this.b = b;
	}

	public Point getC() {
		return c;
	}

	public void setC(Point c) {
		this.c = c;
	}

	public Point getD() {
		return d;
	}

	public void setD(Point d) {
		this.d = d;
	}

	public Point getE() {
		return e;
	}

	public void setE(Point e) {
		this.e = e;
	}

	// 判断能否构成五边形
	public static boolean prime(double m, double n) {
		if (Math.abs(m - n) < 0.001) // 两个数相等
			return true;
		else
			return false;
	}

	public static boolean twoslope(Point a, Point b, Point c) {
		if (prime((c.y - b.y) * (c.x - a.x), (c.y - a.y) * (c.x - b.x)) == true)
			return false;
		else
			return true;
	}

	public int isPentagon() {
		int flag1 = 0;
		if (twoslope(this.a, this.b, this.c) == true && twoslope(this.a, this.b, this.d) == true
				&& twoslope(this.a, this.b, this.e) == true && twoslope(this.a, this.c, this.d) == true
				&& twoslope(this.a, this.c, this.e) == true && twoslope(this.a, this.d, this.e) == true
				&& twoslope(this.b, this.c, this.d) == true && twoslope(this.b, this.c, this.e) == true
				&& twoslope(this.b, this.d, this.e) == true && twoslope(this.c, this.d, this.e) == true) {
			flag1 = 1;
		}
		return flag1;
	}

    //公共区域的面积
	public void samearea() {
		System.out.println("4.0");
	}
   
	// 计算向量的叉乘
	public double multiplicationcross(Point a, Point b, Point c) {
		return (b.getX() - a.getX()) * (c.getY() - a.getY()) - (b.getY() - a.getY()) * (c.getX() - a.getX());
	}

	// 判断能否构成多边形
	public int ispolygon() {
		int flag3 = 0;
		if (twoslope(this.a, this.b, this.c) == false && twoslope(this.b, this.c, this.d) == false
				&& twoslope(this.c, this.d, this.e) == false && twoslope(this.d, this.e, this.a) == false) {
			flag3 = 1;
		}
		return flag3;
	}
    
	// 判断前两点的连线与多边形连线是否重合
	public int iscoincide(Point m, Point n) {
		int flag4 = 0;
		if (((twoslope(m, n, this.a) == false && twoslope(m, n, this.b) == false))
				|| ((twoslope(m, n, this.b) == false && twoslope(m, n, this.c) == false))
				|| ((twoslope(m, n, this.c) == false && twoslope(m, n, this.d) == false))
				|| ((twoslope(m, n, this.d) == false && twoslope(m, n, this.e) == false))
				|| ((twoslope(m, n, this.e) == false && twoslope(m, n, this.a) == false))) {
			flag4 = 1;
		}
		return flag4;
	}
	
	//判断是否为三角形
  
}

 

 

 

 

 

 

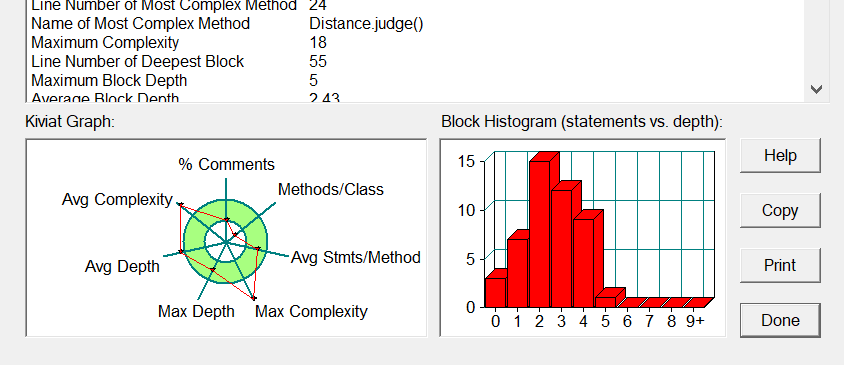
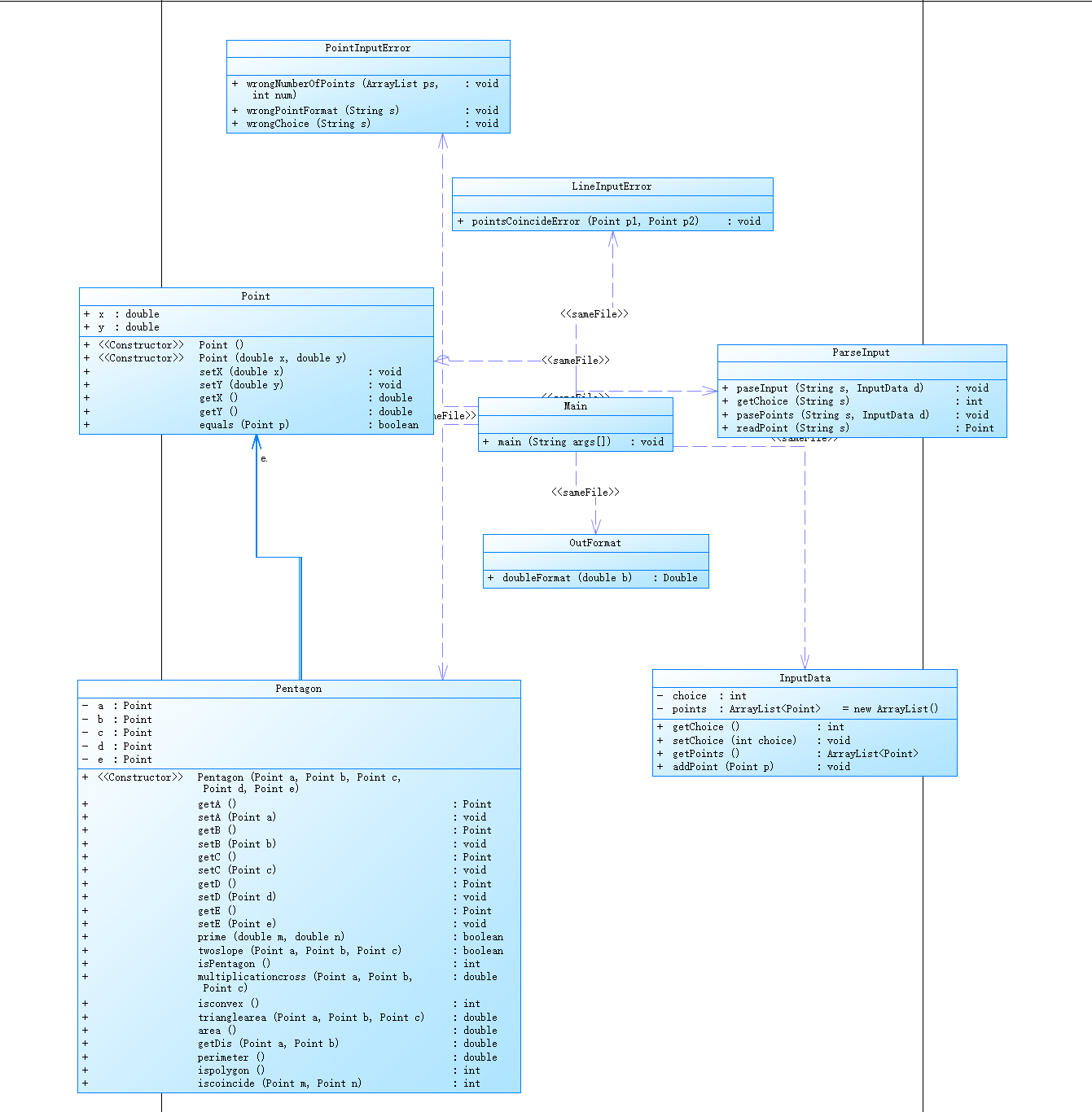
这道题是点线形系列里的最后一道题，也是最复杂的一道题，在上次写四边形时，深刻感受到了方法用不对时的痛苦，所以写这道题时参考了老师的方法，在判断输入是否正确时，先解析坐标，再去判断点的格式和数量，类的划分清晰明了，将正确的点的数量当作参数传进去，直接就可以判断数量是否正确，非常简洁，而且测试点全部通过，后悔太晚发现这个方法了。

这道题和我写的上一道题相比，是一个大跨度，虽然这道题也有很多功能没有实现，但是和四边形比起来，进步是非常大的，自身感觉也不再是一片糊涂了。

但是选项一和选项二有几个测试点没有通过，可能有一些情况没有考虑到，在这也琢磨了很久，改了很多次，但还是没有通过。

后面的一些判断包含关系、计算公共区域面积等选项不是很会写，也希望老师能让我们学一学老师的方法。

 

 3.点与线（类设计）

• 设计一个类表示平面直角坐标系上的点Point，私有属性分别为横坐标x与纵坐标y，数据类型均为实型数，除构造方法以及属性的getter与setter方法外，定义一个用于显示信息的方法display(),用来输出该坐标点的坐标信息，格式如下：(x,y)，数值保留两位小数。为简化题目，其中，坐标点的取值范围设定为(0,200]。若输入有误，系统则直接输出Wrong Format

• 设计一个类表示平面直角坐标系上的线Line，私有属性除了标识线段两端的点point1、point2外，还有一个字符串类型的color，用于表示该线段的颜色，同样，除构造方法以及属性的getter与setter方法外，定义一个用于计算该线段长度的方法getDistance(),还有一个用于显示信息的方法display(),用来输出线段的相关信息。

           题目要求：在主方法中定义一条线段对象，从键盘输入该线段的起点坐标与终点坐标以及颜色，然后调用该线段的display()方法进行输出。

 

我的代码如下：

import java.util.Scanner;

public class Main {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner input = new Scanner(System.in);
		Double x1=input.nextDouble();
		Double y1=input.nextDouble();
		Double x2=input.nextDouble();
		Double y2=input.nextDouble();
		String color=input.nextLine();
		if(x1>0&&x1<=200&&x2>0&&x2<=200&&y1>0&&y1<=200&&y2>0&&y2<=200) {
			Point point1=new Point(x1,y1);
			Point point2=new Point(x2,y2);
			Line line=new Line(point1,point2,color);
			line.display();
		}
		else {
			System.out.println("Wrong Format");
		}
		
	}

}

class Point{
	private double x;
	private double y;
	public Point (){
		
	}
	public Point(double x,double y){
		this.x=x;
		this.y=y;
	}
	public void setX(double x) {
    	this.x=x;
    }
    public double getX() {
    	return x;
    }
    public void setY(double y) {
    	this.y=y;
    }
    public double getY() {
    	return y;
    }
    
    public void display(double x,double y) {
    	String.format("("+"%.2f"+","+"%.2f"+")",x,y);
    }
}

class Line{
	private Point point1;
	private Point point2;
	private String color;
	double x1,y1,x2,y2;

	public Line() {
		
	}
	public Line(Point p1, Point p2,String color) {
        x1=p1.getX();
        y1=p1.getY();
        x2=p2.getX();
        y2=p2.getY();
		this.color = color;
	}
	public void setPoint1(Point point1) {
		this.point1 = point1;
    }
    public Point getPoint1() {
    	return point1;
    }
    public void setPoint2(Point point2) {
		this.point2 = point2;
    }
    public Point getPoint2() {
    	return point2;
    }
    public void setColor(String color) {
    	this.color = color;
    }
    public String getColor() {
    	return color;
    }
    public double getDistance() {
	return Math.sqrt(Math.pow(point1.getX()-point2.getX(),2)+Math.pow(point1.getX()-point2.getX(),2));
    }
    public void display() {
    	System.out.println("The line's color is:"+Color);
    	System.out.println("The line's begin point's Coordinate is:\r\n"+"("+String.format("%.2f",point1.getX())+","+String.format("%.2f",point1.getY())+")");
    	System.out.println("The line's end point's Coordinate is:\r\n"+"("+String.format("%.2f",point2.getX())+","+String.format("%.2f",point2.getY())+")");
    	System.out.println("The line's length is:"+getDistance());
    }
	
}

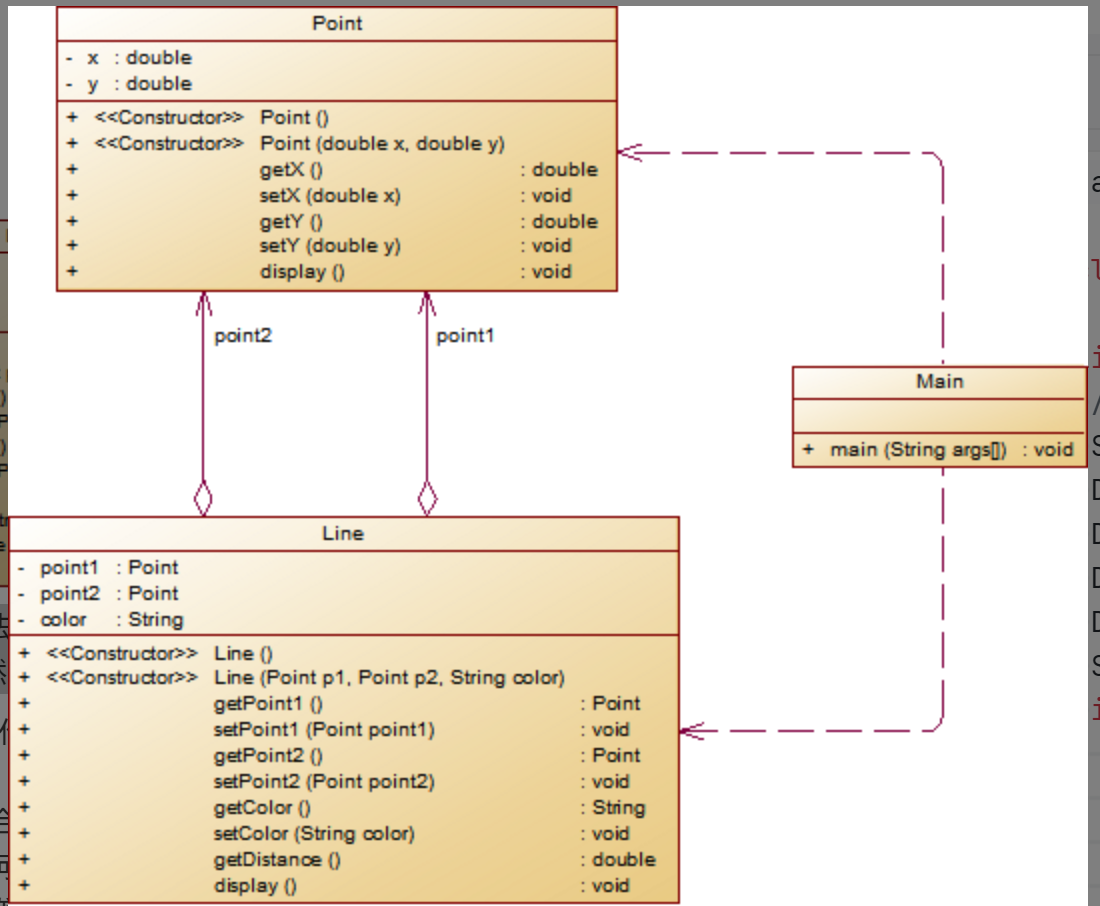
我的类图如下：

 

 

这道题虽然是点与线的题目，跟前面的大作业有点相似，但是题目给出了类的要求，要按老师发的类图来设计，让我感觉有点像之前那次银行业务的题目，就直接按照类图的思路来写就可以，所以并不难。 

 

4.点线面问题重构（继承与多态）

在“点与线（类设计）”题目基础上，对题目的类设计进行重构，以实现继承与多态的技术性需求。

• 对题目中的点Point类和线Line类进行进一步抽象，定义一个两个类的共同父类Element（抽象类），将display()方法在该方法中进行声明（抽象方法），将Point类和Line类作为该类的子类。
• 再定义一个Element类的子类面Plane，该类只有一个私有属性颜色color，除了构造方法和属性的getter、setter方法外，display()方法用于输出面的颜色，输出格式如下：The Plane's color is:颜色
• 在主方法内，定义两个Point（线段的起点和终点）对象、一个Line对象和一个Plane对象，依次从键盘输入两个Point对象的起点、终点坐标和颜色值（Line对象和Plane对象颜色相同），然后定义一个Element类的引用，分别使用该引用调用以上四个对象的display()方法，从而实现多态特性。

 

 

 

我的代码如下：

import java.util.Scanner;

public class Exam2 {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		Scanner input = new Scanner(System.in);
		double x1 = input.nextDouble();
		double y1 = input.nextDouble();
		double x2 = input.nextDouble();
		double y2 = input.nextDouble();
		Point point1 = new Point(x1, y1);
		Point point2 = new Point(x2, y2);
		String color = input.next();
		Line line = new Line(point1, point2, color);
		Plane plane = new Plane(color);
		if (x1 > 0 && x1 <= 200 && x2 > 0 && x2 <= 200 && y1 > 0 && y1 <= 200 && y2 > 0 && y2 <= 200) {
			System.out.println("(" + String.format("%.2f", point1.getX())+ "," + String.format("%.2f", point1.getY()) + ")");
			System.out.println("(" + String.format("%.2f", point1.getX())+ "," + String.format("%.2f", point1.getY()) + ")");
			line.display1();
			point1.display(point2);
			line.display();
			plane.display();
		} else {
			System.out.println("Wrong Format");
		}
	}

}

class Element{
	public Element() {
		
	}
	
	public void display() {
		
	}
}

class Point extends Element{
	private double x;
	private double y;
	
	public Point() {
		
	}
	
	public Point(double x, double y) {
		this.x = x;
		this.y = y;
	}
	
	public void setX(double x) {
		this.x = x;
	}

	public double getX() {
		return x;
	}

	public void setY(double y) {
		this.y = y;
	}

	public double getY() {
		return y;
	}
	
	public void display(Point p) {
		System.out.println("The line's begin point's Coordinate is:\r\n" + "(" + String.format("%.2f", this.getX())
		+ "," + String.format("%.2f", this.getY()) + ")");
		System.out.println("The line's end point's Coordinate is:\r\n" + "(" + String.format("%.2f", p.getX())
		+ "," + String.format("%.2f", p.getY()) + ")");
	}
}


class Line extends Element{
	Point point1;
	Point point2;
	String color;
	
	public Line() {
		
	}
	
	public Line(Point point1, Point point2, String color) {
		this.point1 = point1;
		this.point2 = point2;
		this.color = color;
	}
	
	public void setPoint1(Point point1) {
		this.point1 = point1;
	}

	public Point getPoint1() {
		return point1;
	}

	public void setPoint2(Point point2) {
		this.point2 = point2;
	}

	public Point getPoint2() {
		return point2;
	}

	public void setColor(String color) {
		this.color = color;
	}

	public String getColor() {
		return color;
	}
	
	public double getDis() {
		return Math.sqrt(Math.pow(point1.getX() - point2.getX(), 2) + Math.pow(point1.getX() - point2.getX(), 2));
	}
	
	public void display1() {
		System.out.println("The line's color is:" + getColor());
	}
	
	public void display() {
		System.out.println("The line's length is:" + getDis());
	}
}

class Plane extends Element{
	private String color;
	
	public Plane() {
		
	}
	
	public Plane(String color) {
		this.color = color;
	}
	
	public void setColor(String color) {
		this.color = color;
	}

	public String getColor() {
		return color;
	}
	
	public void display() {
		System.out.println("The plane's color is:" + getColor());
	}
}

　

 

 

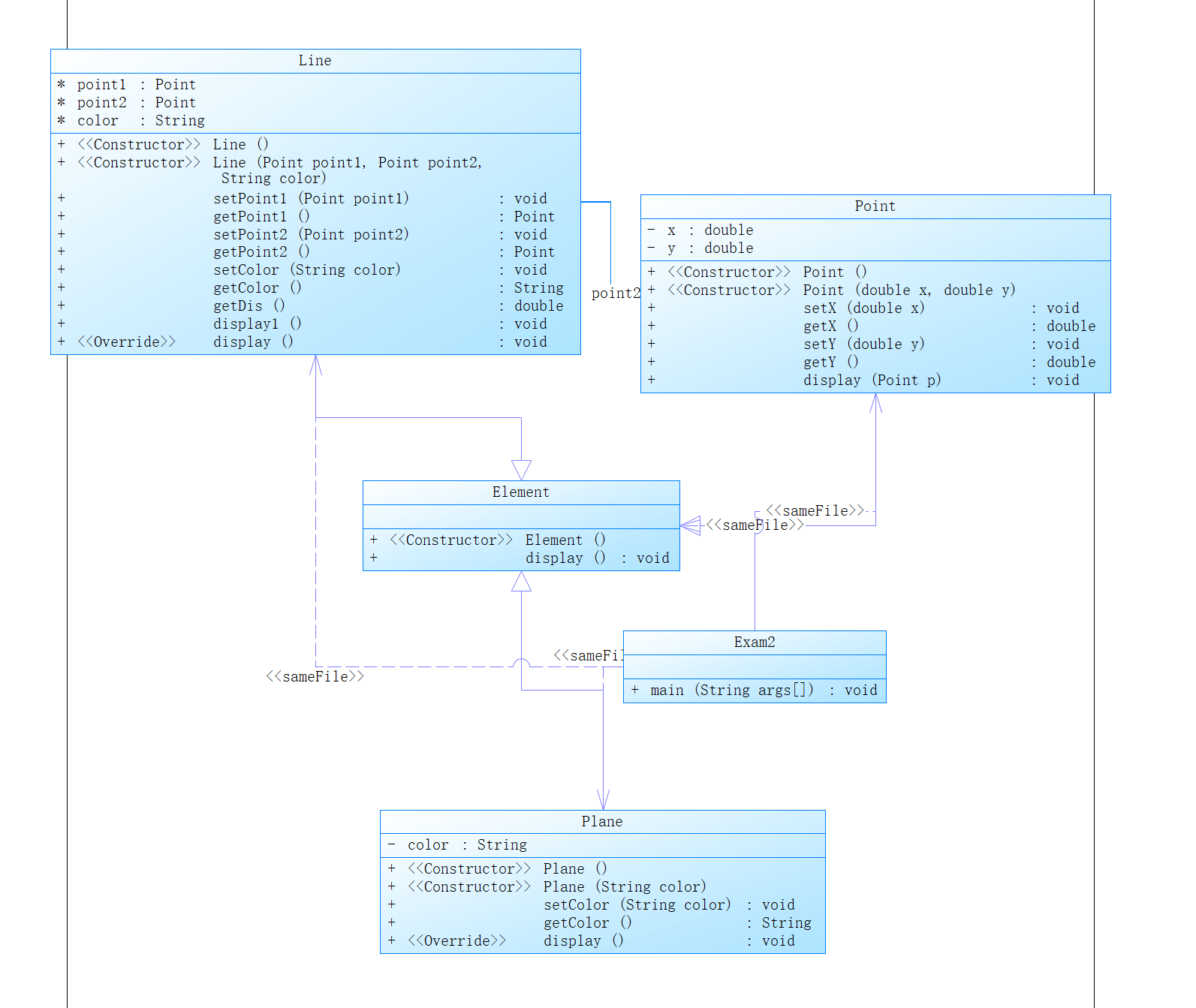
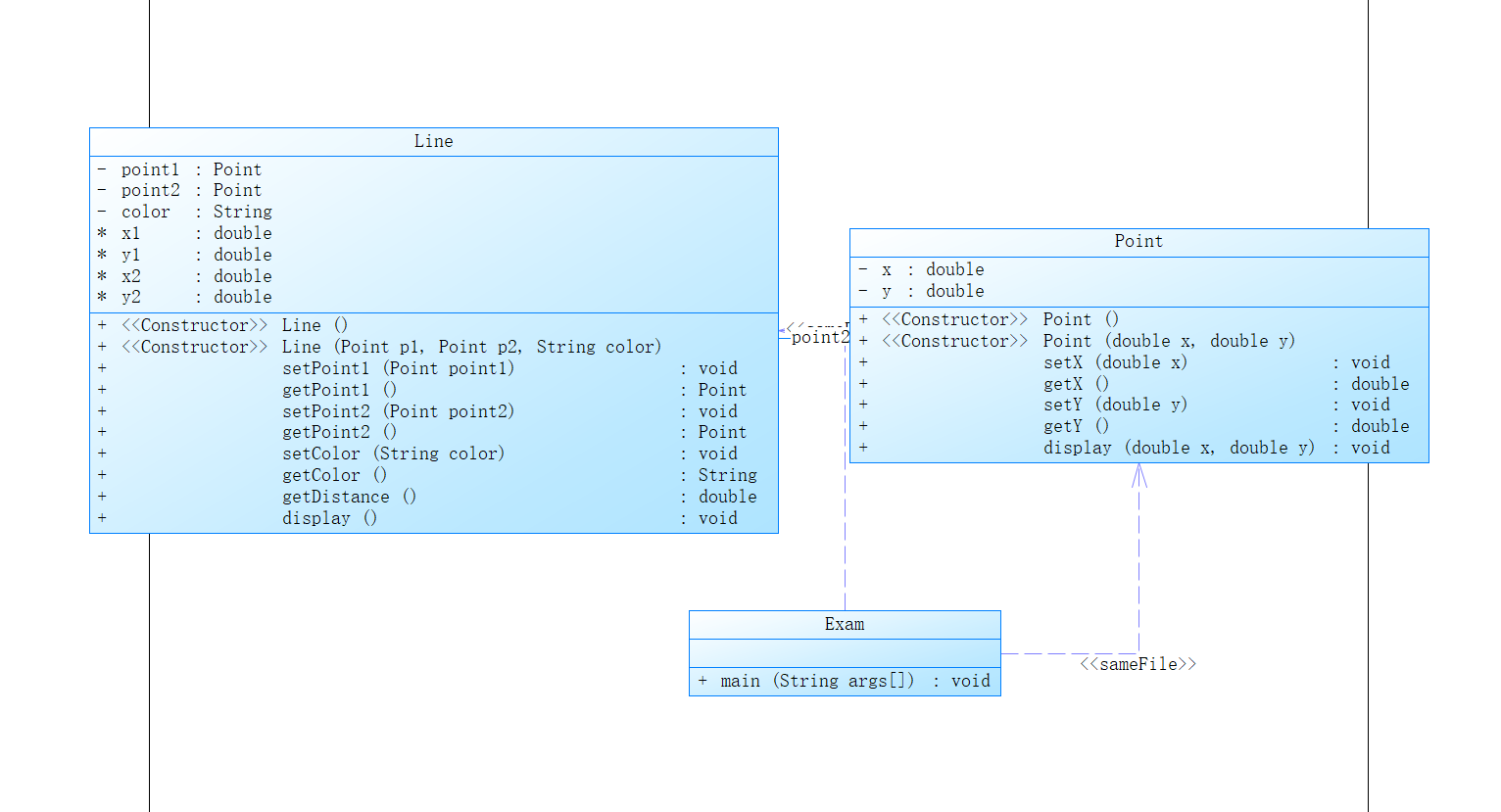
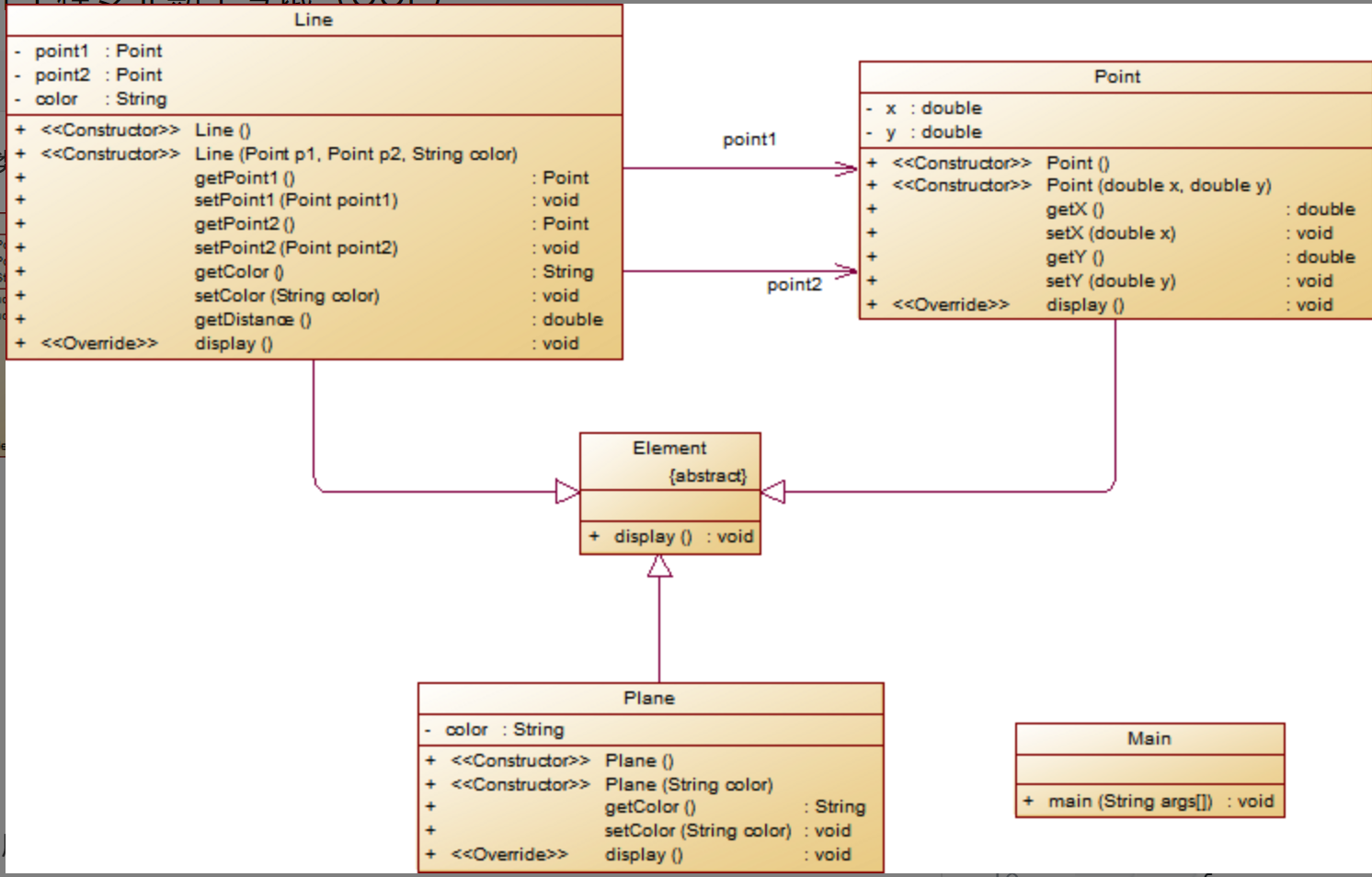
 这是我的代码的类图，和老师的几乎一致，但是事实上可能不太对，因为题中要求分别使用父类调用以上四个对象的display方法，从而实现多态特性，但是我的似乎只用到了继承，在子类中不断的重写display方法，多态并没有体现出来。

在这里需要注意：使用父类类型的引用只想子类的对象；该引用只能调用父类中定义的方法和变量

如果子类中重写（覆盖）了父类中的一个方法，那么在调用这个方法的时候，将会调用子类中的这个方法

变量不能被重写（覆盖），重写只针对方法，如果在子类中重写了父类的变量，编译时会报错

 

5.点线面问题再重构（容器类）

在“点与线（继承与多态）”题目基础上，对题目的类设计进行重构，增加容器类保存点、线、面对象，并对该容器进行相应增、删、遍历操作。

• 在原有类设计的基础上，增加一个GeometryObject容器类，其属性为ArrayList<Element>类型的对象（若不了解泛型，可以不使用<Element>）
• 增加该类的add()方法及remove(int index)方法，其功能分别为向容器中增加对象及删除第index - 1（ArrayList中index>=0）个对象
• 在主方法中，用户循环输入要进行的操作（choice∈[0,4]），其含义如下：
  • 1：向容器中增加Point对象
  • 2：向容器中增加Line对象
  • 3：向容器中增加Plane对象
  • 4：删除容器中第index - 1个数据，若index数据非法，则无视此操作
  • 0：输入结束

这个题目我无从下手，虽然题上给出了详细的类图和介绍，但是我没有学会容器类，不理解ArrayList<Element>类型的对象怎么运用，所以对容器对象的增删、遍历也写不出来。

但是我看了相关资料，在网上找了写的不错的知识点，如果有同学和我一样不会使用这类方法的话，可以一起理解理解这些知识点。

这些知识点是CSDN博主「专注认真努力」写的，总结的非常好，有需要的同学们可以去看看。

https://blog.csdn.net/m0_46692607/article/details/122721264

首先需要理解容器和数组的关系：

1.数组的长度难以扩充，数据的类型必须相同。
2.容器不是数组，不能通过下标的方式访问容器中的元素.
3.数组的所有功能通过Arraylist容器都可以实现，只是实现的方式不同。
4.如果非要将容器当做一个数组来使用，通过toArray方法返回的就是一个数组。

一些常用方法：

boolean add(Object obj):向容器中添加指定的元素
Iterator iterator（）：返回能够遍历当前集合中所有元素的迭代器
Object[] toArray():返回包含此容器中所有元素的数组。
Object get（int index）：获取下标为index的那个元素
Object remove（int index）：删除下标为index的那个元素
Object set（int index,Object element）：将下标为index的那个元素置为element
Object add（int index,Object element）：在下标为index的位置添加一个对象element
Object put(Object key,Object value):向容器中添加指定的元素
Object get（Object key）：获取关键字为key的那个对象
int size():返回容器中的元素数

（3）踩坑心得

1.做题前不要着急开始写代码，一定要花时间去思考一下类的设计方案，好的设计能够起到事半功倍的效果。在前几次写代码时没有意识到这些，看见一道题浅浅思考一下就开始写，导致越往后越复杂，写到最后已经写不下去了，但是往往这个时候已经没有时间了。

2.要会用正则表达式，这里说的会不仅仅是知道表达式怎么写，而是知道该在哪用，怎么去用。在点线形系列的前几道题，我直接对点的个数和格式使用正则表达式，到后面输入六个点甚至十个点时根本无法下笔，而且不同的个数要有不同的写法，非常麻烦。学习了老师的代码，对点先拆分再去匹配，非常清爽简洁，而且能包含所有的情况，测试点都能通过。

3.一定要看清题，不要忽略任何一个信息！有时候写不下去的时候看看题目说不定就想打自己了，因为没看见哪个关键信息。

4.遇到一些数学问题时，不要太自信的自己去想方法，网上有很多简单便捷的方法用起来多香！！不要因为数学问题写不出代码！

(4)改进建议

1.点线形系列前几次的设计都不是很好，在最后一次五边形自己终于领悟到了一些精髓，感觉前面几次类都没有做好，导致后面一些方法都没法复用，还是要修改好多东西，这与面向对象的初衷就背道而驰了...这几道题还可以好好改进一下。

2.一定要多写注释，敲代码时觉得一些方法很简单，不用写注释，可是下次打开看时就该恨自己没有写注释了，要养成多写注释的好习惯。

3.代码尽量写的简洁清爽一些，看起来才会舒服，不要乱七八糟一大堆，要注意布局。

4.当自己认为自己的方法正确，但测试点没有都过时，多看看输出样例，多研究下样例的情况说不定就能发现自己的问题。

5.多用debug调试，总比肉眼看着快，感觉自己不太常用debug，因此总是需要花费好多时间找问题。

（5）总结

  通过完成这几次大作业，感觉确实听课只能学到浅浅的一层，要想真的学会，真的记得一定得去敲代码，自己要去试错，在一次一次的错误中掌握一些方法和技巧，在这个过程中虽然感觉自己深受打击，但不可否认自己确实学会了很多东西，对于面向对象的思考、对类的划分和设计，都是在这一道道题目中积累起来的。

  不管是哪道题，不管它看起来是不是简单，一定要给自己留充足的时间，对题目怀着一颗“敬畏”之心，不能小瞧每一道题目，因为看起来的“简单题”，说不定就令自己花费大量大量的时间还写不完。