CSP2024-S-3-染色

借用了这篇题解的伟大思路。

一个浅显易懂的好思路。

我们可以发现，如果位置 \(i\) 的 \(C_i\) 想要有值，那么他的左边必然存在一个与 \(a_i\) 相等的数，且颜色与 \(a_i\) 的颜色相同。设上一个与 \(a_i\) 相等的数未知为 \(last\)，即 \([last+1,i-1]\) 的颜色与 \(a_i\) 相同。

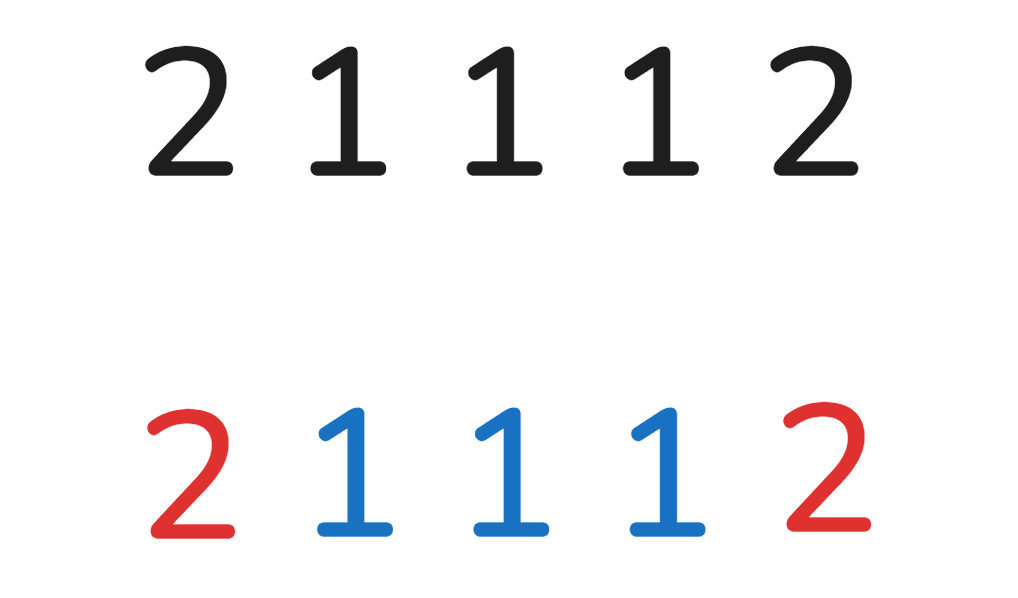
显而易见，对于上述样例最优解如下图所示。那我们可以将 \(i+1\) 位置与 \(j−1\) 位置连接一条边权为 \(a_i\)。

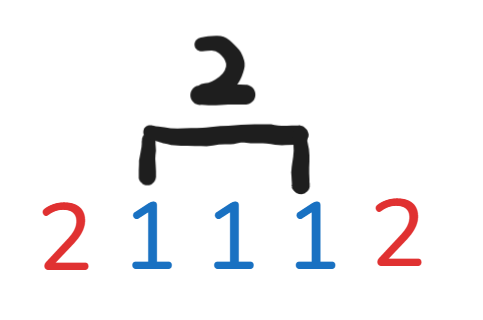
当不相交的边的权值和最大时，即为最优情况。

上图中，三条边都不相交，显然最后输出 \(3\)。

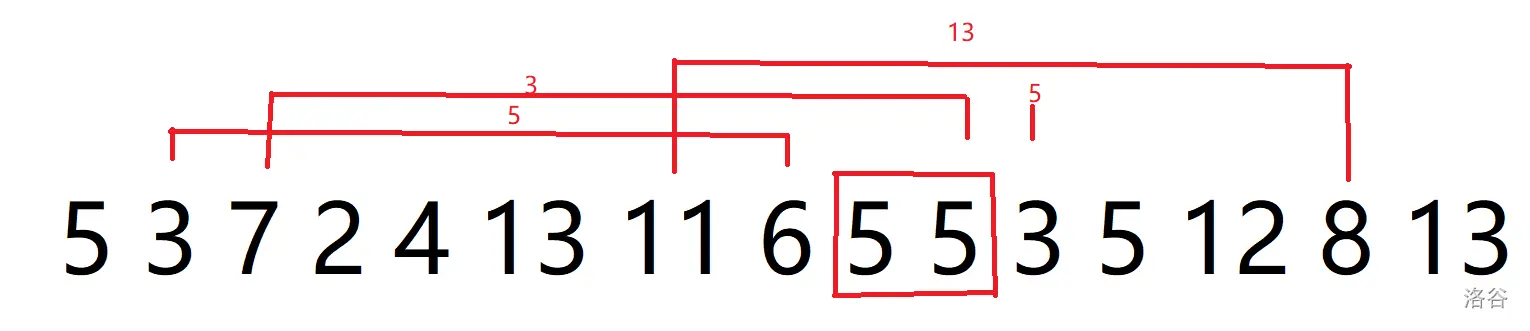
注意这种情况，如果按照我们之前分析的“不相交的边的权值和最大时为最优情况”的话，会输出 \(13\)，这条边最大，但是实际上我们已将第一个 \([6,15]\) 的位置都染成了一种颜色，其中我框起来的第二个 \(5\) 的 \(C_i\) 与之前的 \(5\) 是同一种颜色，所以应输 \(13+5=18\)。

---

如何实现？

我们需要以下数组：

• \(last_i\)：\(i\) 上一个次出现的位置。
• \(e_i\)：以 \(i\) 为终点的连边的起点。
• \(w_i\)：以 \(i\) 为终点的连边的边权。

要么选择这条边，那么就从 \(last_{i−1}\) 位置转移方程。因为这一段都不能选择，线不可以交叉。要么不选择，答案就是上一个点的值。

状态转移方程即为：

\[dp_i=\max(dp_{i-1},dp_{e_i}-1+w_i) \]