搜索
搜索,也就是对状态空间进行枚举,通过穷尽所有的可能来找到最优解,或者统计合法解的个数。
Part 1: dfs
这是不撞南墙不回头的 dfs 喵。
- 全排列
来想一下样例:
输入 3,不难想到,第一次肯定先按 1 2 3 的顺序,那第二次呢?是不是重新在乱排一遍?答案是否定的,不然就没有顺序了。
这个问题像是把 \(n\) 个球放进 \(n\) 个盒子里,有多少种排列方法。
第一轮:第一次 \(1\) 号球放在 \(1\) 号盒里,第二次 \(2\) 号球放在 \(2\) 号盒里,第三次 \(3\) 号球放在 \(3\) 号盒里。
第二轮:把所有球都取出来?不不不,太麻烦。于是先取 \(3\) 号,但是手中只剩 \(3\) 了,遂继续拿一个,将 2 3 交换顺序,变成 3 2。
……
于是得到:
1 2 3
1 3 2
2 1 3
2 3 1
3 1 2
3 2 1
理解了样例,现在来想代码。
如何给小球编号?for 遍历即可。
如果小球已经被使用过了怎么判断?很简单,新建一个 vis 数组标记。
那么我们就能完成一部分了:
for (int i = 1; i <= n; ++i) {
if (!vis[i]) { // 没有使用过
a[x] = i;
vis[i] = 1;
}
}
其中 \(x\) 表示当前处于第 \(x\) 个盒子面前。
AC code
#include <bits/stdc++.h>
#define qwq(i,a,b) for(int i=(a);i<=(b);++i)
#define qaq(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
typedef long long ll;
const int N = 10;
int a[N], vis[N];
int n;
inline void dfs(int x) {
if (x == n + 1) { // 判断边界
qwq (i, 1, n) {
printf("%5d", a[i]);
}
printf("\n");
return ;
}
// 尝试每一种可能
qwq (i, 1, n) {
if (!vis[i]) {
a[x] = i;
vis[i] = 1;
dfs(x + 1); // 继续下一步
vis[i] = 0;
}
}
return ; // 返回
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n;
dfs(1);
}
好的,全排列搞明白了 qwq。
- 迷宫类 dfs
所谓迷宫类 dfs,就是个迷宫……里面有空地、障碍等等。

有的写一个二维数组也可以,顺序也可以交换。
先在我们来模拟一下按 dfs 的思想,该如何摸到终点。

这就是第一条线路,那么第二条自然就是从终点前回溯了,return 即可。
这样有可能不是最优解,怎么办?在每次到终点时都记录一下步数,取最小值即可。
板子题:
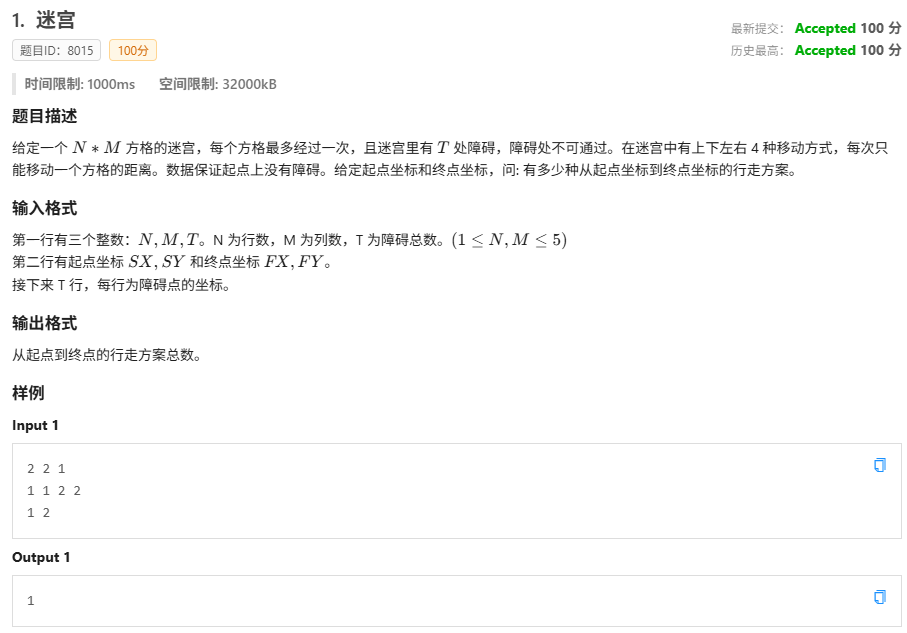
Code
#include <bits/stdc++.h>
#define qwq(i,a,b) for(int i=(a);i<=(b);++i)
#define qaq(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
typedef long long ll;
const int N = 10;
int dx[] = {0, 0, -1, 1};
int dy[] = {-1, 1, 0, 0};
int mapn[N][N], vis[N][N];
int n, m, t;
int sx, sy, fx, fy;
int cnt;
inline void dfs(int x, int y) {
if (x == fx && y == fy) {
cnt++;
return ;
}
qwq (i, 0, 3) {
int now_x = x + dx[i];
int now_y = y + dy[i];
if (now_x < 1 || now_x > n || // 地图边界外
now_y < 1 || now_y > m || // 地图边界外
vis[now_x][now_y] == 1 || // 访问过
mapn[now_x][now_y] == 1) // 障碍
{
continue;
}
vis[now_x][now_y] = 1;
dfs(now_x, now_y);
vis[now_x][now_y] = 0;
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m >> t;
cin >> sx >> sy >> fx >> fy;
vis[sx][sy] = 1;
while (t--) {
int x, y;
cin >> x >> y;
mapn[x][y] = 1;
}
dfs(sx, sy);
cout << cnt;
}

太简单了,直接给代码,思路在注释里。
#include <bits/stdc++.h>
#define qwq(i,a,b) for(int i=(a);i<=(b);++i)
#define qaq(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
typedef long long ll;
const int N = 105;
int dx[] = {0, 0, -1, 1};
int dy[] = {-1, 1, 0, 0};
char mapn[N][N];
int vis[N][N];
int n, m, t;
int sx, sy, fx, fy;
int ans = INT_MAX;
inline void dfs(int x, int y, int sum) {
if (sum >= ans) return ; // 小剪枝:如果当前步数已经 >= 答案,那么不需要继续走到终点,直接回溯即可
if (x == fx && y == fy) {
ans = min(ans, sum);
return ;
}
qwq (i, 0, 3) {
int now_x = x + dx[i];
int now_y = y + dy[i];
if (now_x < 1 || now_x > n || // 地图边界外
now_y < 1 || now_y > m || // 地图边界外
vis[now_x][now_y] == 1 || // 访问过
mapn[now_x][now_y] == '#') // 障碍
{
continue;
}
vis[now_x][now_y] = 1;
dfs(now_x, now_y, sum + 1);
vis[now_x][now_y] = 0;
}
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
qwq (i, 1, n) {
qwq (j, 1, m) {
cin >> mapn[i][j];
}
}
cin >> sx >> sy >> fx >> fy;
vis[sx][sy] = 1;
dfs(sx, sy, 0);
if (ans == INT_MAX) cout << -1;
else cout << ans;
}
Part 2: bfs
这哥们没那么憨,不会像 dfs 一样不撞南墙不回头。
他会在每一个岔路口都向前走一个,所以也叫宽度优先搜索。
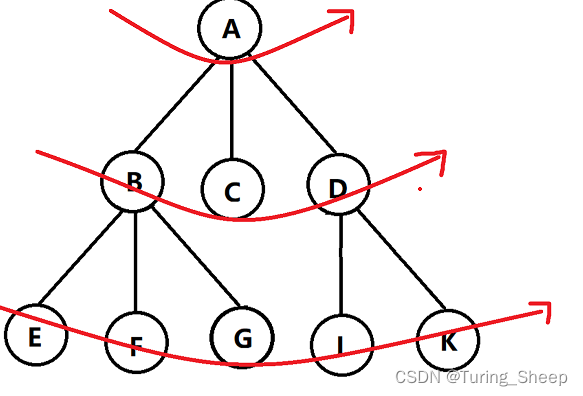
既然他每次都向前走一个,说明 bfs 它是具有最短路的性质的。
Why?
因为每次搜索的位置都是距离当前节点最近的点。每次选择路线都是在之前基础上的最优解,由此积累,就可以由局部最优推出整体最优。
有点像贪心的思想。
所以再走迷宫时,每次出发的时候,走到离自己最近的点,由此我们每次都保证走最近的,那从局部最近推整体最近,必有一条路是整体最近的,所以我们可以利用 bfs 做最短路问题。
- 迷宫最小步数
怎么实现 bfs 的思想?由于 bfs 的第一件事就是我们需要先走最近的,可以用队列这个数据结构。
那么《迷宫最小步数-弱化版》就可以这么写:
#include <bits/stdc++.h>
#define qwq(i,a,b) for(int i=(a);i<=(b);++i)
#define qaq(i,a,b) for(int i=(a);i>=(b);--i)
using namespace std;
typedef long long ll;
const int N = 100;
int dx[] = {0, 0, -1, 1};
int dy[] = {-1, 1, 0, 0};
char mapn[N][N];
int vis[N][N];
int n, m, t;
int sx, sy, fx, fy;
int ans = INT_MAX;
struct node {
int x, y;
int cnt;
};
inline void bfs() {
memset(vis, 0, sizeof vis); // 初始化,表示没来过
queue<node> qu;
qu.push({sx, sy, 0}); // 起点入队
while (!qu.empty()) {
node now = qu.front(); // 队头元素
qu.pop();
if (now.x == fx && now.y == fy) {
cout << now.cnt;
exit(0);
}
qwq (i, 0, 3) {
int now_x = now.x + dx[i];
int now_y = now.y + dy[i];
int now_cnt = now.cnt + 1;
if (now_x < 1 || now_x > n || // 地图边界外
now_y < 1 || now_y > m || // 地图边界外
vis[now_x][now_y] == 1 || // 访问过
mapn[now_x][now_y] == '#') // 障碍
{
continue;
}
qu.push({now_x, now_y, now_cnt});
vis[now_x][now_y] = 1;
}
}
cout << -1;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0), cout.tie(0);
cin >> n >> m;
qwq (i, 1, n) {
qwq (j, 1, m) {
cin >> mapn[i][j];
}
}
cin >> sx >> sy >> fx >> fy;
bfs();
}
- 联通块问题
什么是联通块问题?像P1331 海战。
这里一艘艘船是联通的,组成了一个大图形。我们可以尝试搜索每一个 #,把与它联通的船都标记为 .,这样就不会再重复搜索同一个联通块了。
Some Code
inline void bfs(int x, int y) {
mapn[x][y] = '.'; // 标记为水
queue<node> qu;
qu.push({x, y}); // 起点入队
while (!qu.empty()) {
node now = qu.front(); // 队头元素
qu.pop();
qwq (i, 0, 3) {
int now_x = now.x + dx[i];
int now_y = now.y + dy[i];
if (now_x < 1 || now_x > n || // 地图边界外
now_y < 1 || now_y > m || // 地图边界外
mapn[now_x][now_y] == '.') // 水
{
continue;
}
mapn[now_x][now_y] = '.';
qu.push({now_x, now_y});
}
}
}
Part 3: 搜索剪枝
可行性剪枝: 当前状态根本不可能达到目标状态,提前回溯或不加入队列。
最优性剪枝 (主要针对 dfs 求最优解): 当前状态不可能达到比已知最优解更好的解,提前回溯。
还可以用记忆化搜索,会在 Part 4 里讲。
可以多做练习,比如P1120 小木棍。
我的题解:link
还没讲完讲完了 qaq,点个赞喵。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号