00八大数学思维方法

分析、综合、抽象、概括、归纳、演绎、化归、类比

抽象是最难的

基于中学数学的认知能力，展示数学的哲学方法，从数学文化的高度来看中学数学。
从何体会数学的美。

归纳

从一般到特殊，从部分到整体。
归纳证明法的步骤：
1.计算n=1，是否成立
2.假设n=k ，成立
3.计算 n = K+1 ，是否成立
n=1 成立 如果 n=k 成立时 n=k+1 成立，则可以得出结论，n在任意情况下都成立。 证毕。

抽象

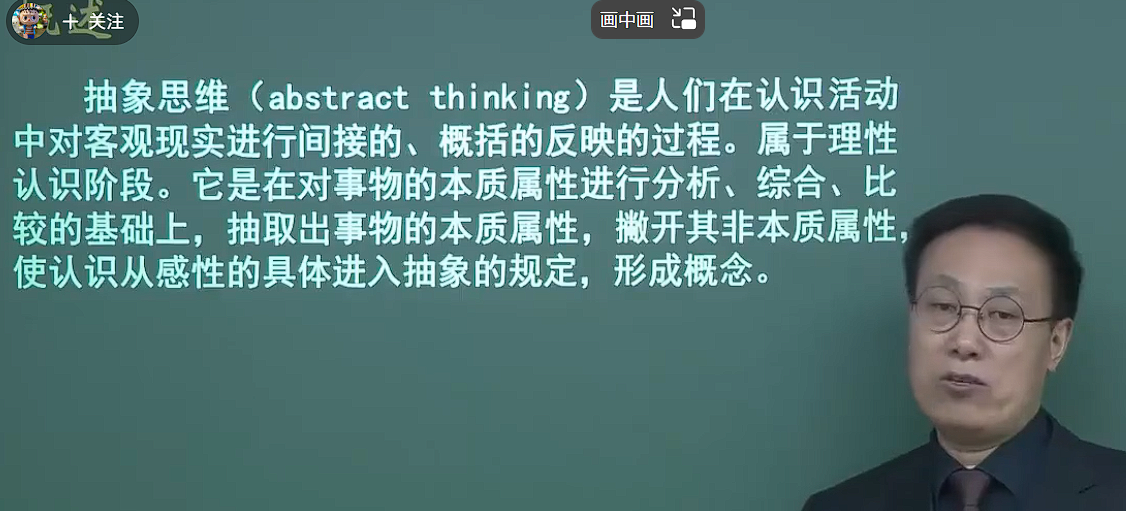
也即是把现实生活中的问题，用数学模型进行匹配，从来来解决现实生活中的问题。
比如知道速度，回答从家到机场的时间。
抽象这个真有点难，抽象思维不简单。

演绎法

数学的演绎法是一种推理方法，它从一般性的前提或公理出发，通过逻辑推导得出特定的结论。演绎法是建立在形式逻辑基础之上的，其核心思想是从已知的一般性原理中推出具体的特殊结果。

在数学证明中，演绎法是非常重要的工具。一个典型的数学证明通常包括以下步骤：

前提陈述：列出需要使用的公理、定理或先前已经证明过的命题作为推理的基础。
推理过程：使用逻辑连接词（如“因此”、“所以”等）和符号表示（如蕴含箭头⇒）来展示如何从前提一步步地推导出新的命题。
结论陈述：最后得出的命题就是所要证明的结果。
演绎法与归纳法相对，归纳法是从个别例子出发，试图概括出一般规律。而演绎法则相反，它是从一般规律出发去验证特殊情况。演绎推理具有确定性和必然性，即如果前提是正确的，则结论也一定是正确的。

在离散数学中，演绎法被广泛应用于各种概念和定理的证明，比如集合论、图论、数理逻辑等领域。通过演绎法，我们可以确保数学理论的严谨性和一致性。
演绎证明是从一般到特殊的方法。
其证明过程是 如果 A --> B,那么 A 的子集a 一定可以 --> B 。
比如 人 会 死 。苏格拉底是人，所以苏格拉底 会死。
A 是 一般性原理，B 结论，a 是特殊性原理。
演绎证明法的步骤：
1 找到成立的大前提，即一般性原理
2 证明 特殊性原理是 大前提的子集
3 所以结论成立。

化归

化归是数学中的一种基本思想和方法，它是指在解决问题的过程中，不是直接解决原问题，而是通过一系列变换或转化，将原问题转化为一个或多个已知的、更容易处理的问题。这种转化的过程通常涉及对问题的重新表述或者对问题结构的深入理解，以便将其转换为另一种形式。

化归的核心要素包括：

化归对象：确定需要进行转化的具体内容，即要从哪个问题开始进行化归。
化归手段：选择合适的转化方法，这可能包括使用定义、定理、性质、公式等数学工具。
化归目标：明确转化后的结果应该是什么样的问题，通常是已经解决或易于解决的问题。
化归法的应用广泛，例如在代数中，四次方程可以通过转化变为双二次方程来求解；在几何中，复杂形状的面积计算可以转化为简单图形的面积之和等等。此外，化归思想也常常用于教学中，帮助学生理解和掌握新概念，以及如何用已知的知识去解决新的问题。

类比

类比是一种推理方法，并不是一种严格的证明方法
数学的类比是一种推理方法，它通过比较两个或多个不同但相似的对象、过程或概念来获得新的理解和发现。类比法可以帮助人们从已知的知识领域扩展到未知的领域，或者从简单的例子中提取出更一般性的原理。

在数学中，类比常常用于启发思考和提出猜想。例如，当研究一个新的数学对象时，我们可以寻找与之类似但已经充分理解的对象，并尝试将对后者的一些性质和结论应用到新对象上。这种思想有时能够引导我们找到解决问题的新方法，甚至发现一些重要的定理或规律。

需要注意的是，虽然类比可以提供有用的线索和启示，但它并不是一种严格的证明方法。基于类比提出的猜想需要进一步用演绎法进行证明才能成为可靠的数学结果。

举个例子，欧拉在研究多面体的顶点数（V）、边数（E）和面数（F）之间的关系时，他观察到了凸多面体中的简单情况（如正四面体、正方体等），并注意到这些情况下都满足公式 V - E + F = 2。然后他通过类比，猜测这个公式对于所有凸多面体都成立，这就是著名的欧拉公式。然而，要使这个猜想成为定理，还需要对其进行严谨的证明。