红黑树（未完待续）

前言：

从一开始的二叉树：最多有两个子节点

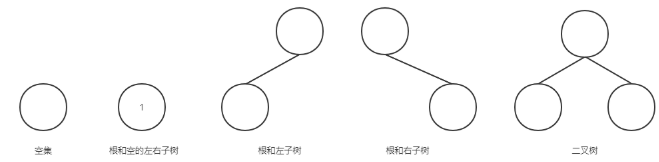
二叉树有五种形态：

+排序-----二叉（排序、查找）树（BST）

采用中序方式排序，通过类似于二分查找的方式，减少时间复杂度
缺点：出现斜树时，无用

++平衡-----平衡二叉（排序）树（AVL）

平衡：指插入、删除元素后可以自平衡的二叉查找树。我们平衡的手段-----旋转。
AVL树：任意节点的两个子树的高度差不超过1的平衡树
缺点：
1.当数据量大时，不够直观，比如：

2.插入删除的时候自平衡 太复杂

于是延伸出很多其他的树，比如2-3树，2-3-4树（磁盘读取的便利，减少时间复杂度），B树（2-3-4-...树），红黑树

红黑树

1.定义/性质

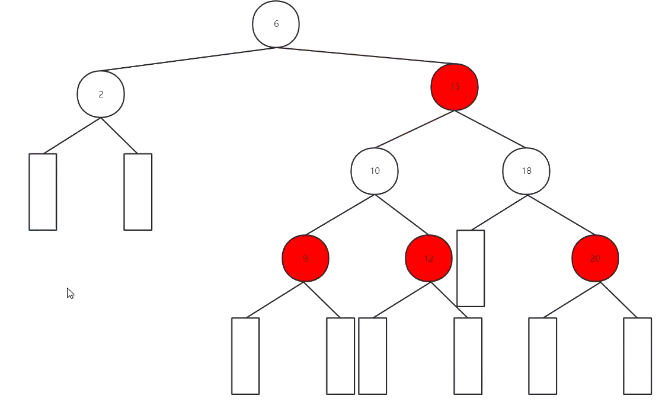
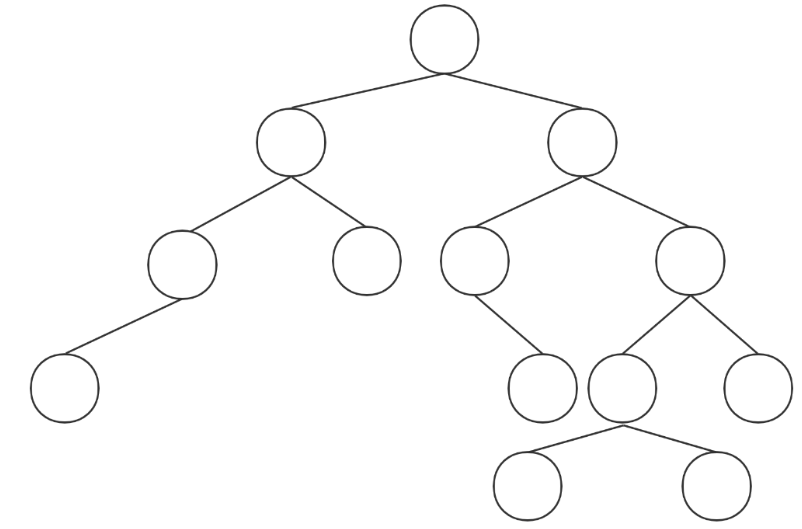
这是一颗红黑树,

结点是红或黑色
根节点是黑色
叶子结点是黑色，NULL
根节点到叶子结点的路径中无连续的红色结点
从任何结点到叶子结点的所有路径，包含相同数目的黑色结点

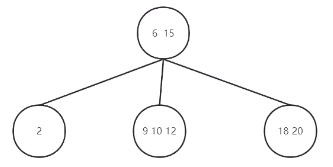
红黑树是一种特殊的平衡树，如上图可以转变成2-3-4树，高度降低，大大降低了查找删除等的时间复杂度.
相较于AVL树，在大量的增删操作下，红黑树有明显的优势

符合局部不平衡。why？？

概念

• 黑高
  任意结点上的黑高，该节点到叶子（黑）结点路径上的黑色结点数量，不包括该节点本身。

这个不包括：只是一种统一规定而已，类似于平衡树的高度从0开始

特点
分类

二. 插入

1. 旋转
2. 着色

着色不成功再旋转，要关注父亲结点的亲戚们

x是新插入的结点

1. 先标准BST（二叉排序树）插入
2. 若x是根节点，转换为黑色（默认是红色）

那根节点不是黑色NULL吗

3. 当x的父亲结点p为红色
   （x不是根节点）

x:插入结点
p：父亲结点
u：父亲结点的兄弟结点---叔叔结点

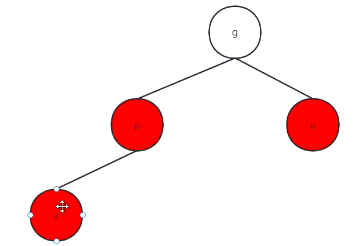
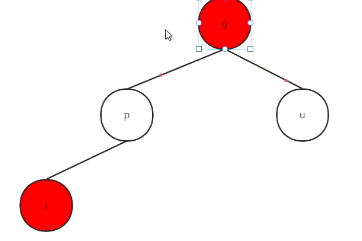
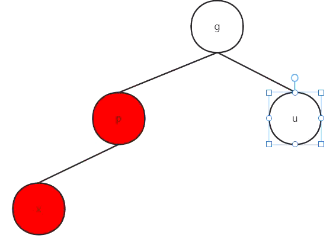
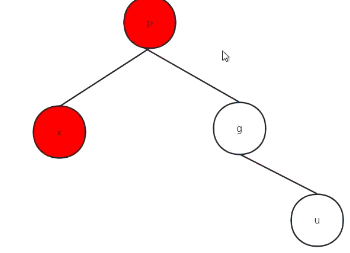
• 叔叔结点u为红色：
  把p和u结点全变黑色，爷爷节点变红。
  接着把爷爷节点（红）看做x结点，向上接着检查，直至根节点。（根节点一直为黑）
  
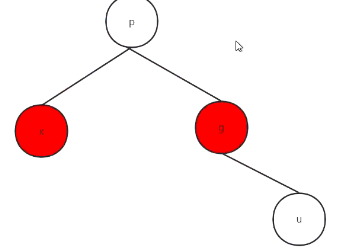
  转变后：
  

类型2：

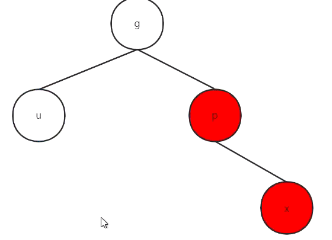
左旋

再交换颜色

• 叔叔结点u是黑色结点
  
  右旋：
  
  交换颜色：
  

下面演示 当局部不平衡时，立马能平衡回来：

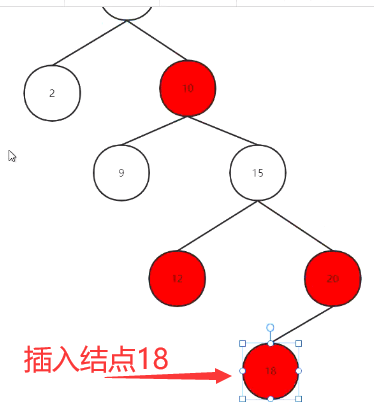
先给12（u结点），20（p结点），15（g结点）着色，

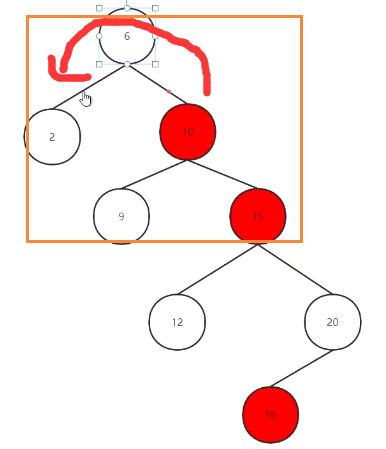
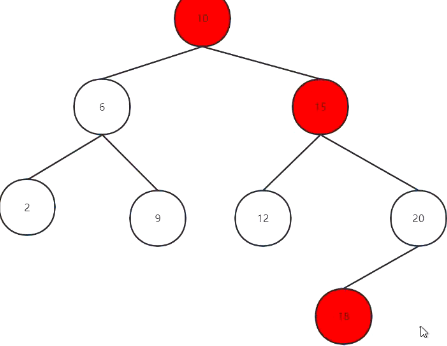
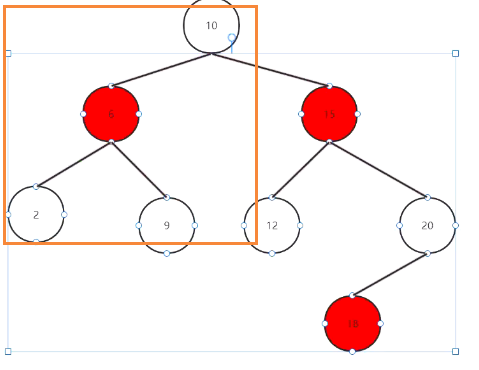
删除有空再写...