二叉排序树的查找、插入、删除操作

二叉树的一些操作

二.二叉排序树

1.查找

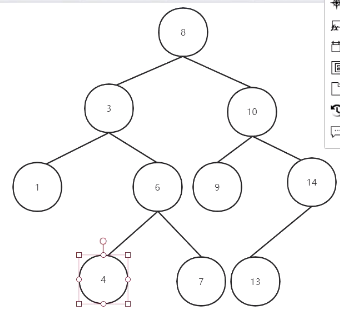
分析：
比如要查找6，
root先指向根节点8，
因为（6<8），所以root指向8的左边子节点 3
又（6>3），所以root指向3的右子节点 6
查找完成。

代码如下：

点击查看代码

/**
     * 二叉排序树的查找操作
     * @param root 根节点
     * @param data 待查找的元素
     * @return
     */
    public Boolean search(Node_cp root ,int data){
        while(root != null){
            if(data == root.data){
                return true;
            }
            if(data < root.data){
                root = root.child;
            }else{
                root = root.sibling;
            }
        }
        return false;
    }

#### 2.插入

插入和查找很像，再加上一个prev——记录待待插入结点的父节点（上个结点）

点击查看代码

/**
     * 二叉排序树的插入操作
     * @param root
     * @param data
     */
    public void insert(Node_cp root,int data){
        Node_cp prev = null;//
        while(root != null){
            prev = root;
            if(data < root.data){
                root = root.child;
            }
            else if(data > root.data){
                root = root.sibling;
            }else{
                return;
            }
        }
        //此时root指向null，prev指向要插入结点的父节点，即root的上一个结点
        if(prev.data > data){
            prev.child = new Node_cp(data);
        }else{
            prev.sibling = new Node_cp(data);
        }
    }

#### 3.删除操作

分析：

1. 待删结点只有一个左或右子节点
   将子节点重新连入被删除处即可

2. 待删结点是叶子结点，就直接删

3. 待删除结点有左右两个结点
   比如删除上图中的8（根节点）
   按中序排序的话该图是： 134678 9 10 13 14
   所以，可以将7或者9填充到8这个位置上。

因此
先找到待删结点的左子树的最大值（7）,将其替换上去
或者（...）
找右子树的最小值（9）替换上去。
这么操作，将不会破坏二叉排序树的规则。