前端 数学计算 big.js 使用
解决0.1 + 0.2 不等于 0.3的问题
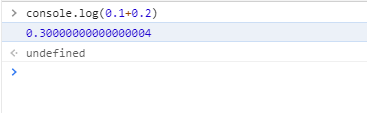
解决方法
方法一,同时扩大倍数再除以相同的倍数
0.1 +0.2 // 0.30000000000000004 (0.1 *10 + 0.2 *10) / 10 // 0.3
方法二,第三方库
bignumber.js
math.js
big.js
big.js 基础用法
运算
// 运算 // const plus = Big(0.1).plus(0.2); // 加 // const minus = Big(0.3).minus(0.1); // 减 // const mul = Big(10.22).times(100); // 乘 // const div = Big(2.4).div(0.8); // 除
toFixed
function toFixed(val, len) {
return new Big(val).toFixed(len);
}
自己的tofixed
// toFixed 修复 function toFixed(number, precision) { // var precision = precision; if (typeof precision == 'undefined') { precision = 2; } if (precision == 0) { return parseInt(+number); } number = Math.round(+number + 'e' + precision) / Math.pow(10, precision) + ''; let s = number.split('.'); if ((s[1] || '').length < precision) { s[1] = s[1] || ''; s[1] += new Array(precision - s[1].length).fill('0').join(''); } return s.join('.'); }
tofixed 测试
console.log('1 -- 默认', toFixed(1)); //1.00
// console.log('1 -- 2位', toFixed(1, 2)); //1.00
// console.log('1 -- 0位', toFixed(1, 0)); //1
// console.log('1.005 --2位', toFixed(1.005, 2)); //1.01
// console.log('1.009 --2位', toFixed(1.009, 2)); //1.01
// console.log('1.050 --2位', toFixed(1.05, 2)); //1.05
// console.log('1.15 --2位', toFixed(1.15, 2)); //1.15
// console.log('1.215 --2位', toFixed(1.215, 2)); //1.22
// console.log('1.245 --2位', toFixed(1.245, 2)); //1.25
// console.log('1.255 --2位', toFixed(1.255, 2)); //1.26
// console.log('---------2 位数------------- ');
// console.log('12.205--', toFixed(12.205, 2)); // 预期 '12.21'
// console.log('12.215--', toFixed(12.215, 2)); // 预期 '12.22'
// console.log('12.225--', toFixed(12.225, 2)); // 预期 '12.23'
// console.log('12.235--', toFixed(12.235, 2)); // 预期 '12.24'
// console.log('12.245--', toFixed(12.245, 2)); // 预期 '12.25'
// console.log('12.255--', toFixed(12.255, 2)); // 预期 '12.26'
// console.log('12.265--', toFixed(12.265, 2)); // 预期 '12.27'
// console.log('12.275--', toFixed(12.275, 2)); // 预期 '12.28'
// console.log('12.285--', toFixed(12.285, 2)); // 预期 '12.29'
// console.log('12.295--', toFixed(12.295, 2)); // 预期 '12.30'
~~ 位运算 转成 整数,去掉小数部分
var a = '123';
console.log(~~a); //输出123
var b = 'asd';
console.log(~~b); //输出0
// ~~-1.1 == -1
// ~~true == 1
// ~~false == 0
// ~~"" == 0
// ~~[] == 0
// ~~{} == 0
// ~~undefined ==0
// ~~!undefined == 1
// ~~null == 0
// ~~!null == 1
// ~~NaN == 0
~是取反两次。 ~~的作用是去掉小数部分,因为位运算的操作值要求是整数,其结果也是整数,所以经过位运算的都会自动变成整数。
注意事项 Big 数字不会被它的方法改变。
// Big 数字不会被它的方法改变。 // 0.3 - 0.1 // 0.19999999999999998 // x = new Big(0.3) // x.minus(0.1) // "0.2" // x // "0.3"
big.js 二次封装 循环数组计算
function calculate(arr, prop) {
var prop = prop || "plus"
var arr = arr
var mm = new Big(arr[0]);
var pre = mm;
for (let i = 1; i < arr.length; i++) {
pre = pre[prop](arr[i])
}
return Number(pre)
}
console.log("for 加多次", calculate([8, 2, 1], "plus")) //11
console.log("for 减多次", calculate([8, 2, 1], "minus")) //5
console.log("for 乘多次", calculate([8, 2, 1], "mul")) //16
console.log("for 除多次", calculate([8, 2, 1], "div")) //4
工具源码
/*
* big.js v6.2.1
* A small, fast, easy-to-use library for arbitrary-precision decimal arithmetic.
* Copyright (c) 2022 Michael Mclaughlin
* https://github.com/MikeMcl/big.js/LICENCE.md
*/
var Big,
/************************************** EDITABLE DEFAULTS *****************************************/
// The default values below must be integers within the stated ranges.
/*
* The maximum number of decimal places (DP) of the results of operations involving division:
* div and sqrt, and pow with negative exponents.
*/
DP = 20, // 0 to MAX_DP
/*
* The rounding mode (RM) used when rounding to the above decimal places.
*
* 0 Towards zero (i.e. truncate, no rounding). (ROUND_DOWN)
* 1 To nearest neighbour. If equidistant, round up. (ROUND_HALF_UP)
* 2 To nearest neighbour. If equidistant, to even. (ROUND_HALF_EVEN)
* 3 Away from zero. (ROUND_UP)
*/
RM = 1, // 0, 1, 2 or 3
// The maximum value of DP and Big.DP.
MAX_DP = 1E6, // 0 to 1000000
// The maximum magnitude of the exponent argument to the pow method.
MAX_POWER = 1E6, // 1 to 1000000
/*
* The negative exponent (NE) at and beneath which toString returns exponential notation.
* (JavaScript numbers: -7)
* -1000000 is the minimum recommended exponent value of a Big.
*/
NE = -7, // 0 to -1000000
/*
* The positive exponent (PE) at and above which toString returns exponential notation.
* (JavaScript numbers: 21)
* 1000000 is the maximum recommended exponent value of a Big, but this limit is not enforced.
*/
PE = 21, // 0 to 1000000
/*
* When true, an error will be thrown if a primitive number is passed to the Big constructor,
* or if valueOf is called, or if toNumber is called on a Big which cannot be converted to a
* primitive number without a loss of precision.
*/
STRICT = false, // true or false
/**************************************************************************************************/
// Error messages.
NAME = '[big.js] ',
INVALID = NAME + 'Invalid ',
INVALID_DP = INVALID + 'decimal places',
INVALID_RM = INVALID + 'rounding mode',
DIV_BY_ZERO = NAME + 'Division by zero',
// The shared prototype object.
P = {},
UNDEFINED = void 0,
NUMERIC = /^-?(\d+(\.\d*)?|\.\d+)(e[+-]?\d+)?$/i;
/*
* Create and return a Big constructor.
*/
function _Big_() {
/*
* The Big constructor and exported function.
* Create and return a new instance of a Big number object.
*
* n {number|string|Big} A numeric value.
*/
function Big(n) {
var x = this;
// Enable constructor usage without new.
if (!(x instanceof Big)) return n === UNDEFINED ? _Big_() : new Big(n);
// Duplicate.
if (n instanceof Big) {
x.s = n.s;
x.e = n.e;
x.c = n.c.slice();
} else {
if (typeof n !== 'string') {
if (Big.strict === true && typeof n !== 'bigint') {
throw TypeError(INVALID + 'value');
}
// Minus zero?
n = n === 0 && 1 / n < 0 ? '-0' : String(n);
}
parse(x, n);
}
// Retain a reference to this Big constructor.
// Shadow Big.prototype.constructor which points to Object.
x.constructor = Big;
}
Big.prototype = P;
Big.DP = DP;
Big.RM = RM;
Big.NE = NE;
Big.PE = PE;
Big.strict = STRICT;
Big.roundDown = 0;
Big.roundHalfUp = 1;
Big.roundHalfEven = 2;
Big.roundUp = 3;
return Big;
}
/*
* Parse the number or string value passed to a Big constructor.
*
* x {Big} A Big number instance.
* n {number|string} A numeric value.
*/
function parse(x, n) {
var e, i, nl;
if (!NUMERIC.test(n)) {
throw Error(INVALID + 'number');
}
// Determine sign.
x.s = n.charAt(0) == '-' ? (n = n.slice(1), -1) : 1;
// Decimal point?
if ((e = n.indexOf('.')) > -1) n = n.replace('.', '');
// Exponential form?
if ((i = n.search(/e/i)) > 0) {
// Determine exponent.
if (e < 0) e = i;
e += +n.slice(i + 1);
n = n.substring(0, i);
} else if (e < 0) {
// Integer.
e = n.length;
}
nl = n.length;
// Determine leading zeros.
for (i = 0; i < nl && n.charAt(i) == '0';) ++i;
if (i == nl) {
// Zero.
x.c = [x.e = 0];
} else {
// Determine trailing zeros.
for (; nl > 0 && n.charAt(--nl) == '0';);
x.e = e - i - 1;
x.c = [];
// Convert string to array of digits without leading/trailing zeros.
for (e = 0; i <= nl;) x.c[e++] = +n.charAt(i++);
}
return x;
}
/*
* Round Big x to a maximum of sd significant digits using rounding mode rm.
*
* x {Big} The Big to round.
* sd {number} Significant digits: integer, 0 to MAX_DP inclusive.
* rm {number} Rounding mode: 0 (down), 1 (half-up), 2 (half-even) or 3 (up).
* [more] {boolean} Whether the result of division was truncated.
*/
function round(x, sd, rm, more) {
var xc = x.c;
if (rm === UNDEFINED) rm = x.constructor.RM;
if (rm !== 0 && rm !== 1 && rm !== 2 && rm !== 3) {
throw Error(INVALID_RM);
}
if (sd < 1) {
more =
rm === 3 && (more || !!xc[0]) || sd === 0 && (
rm === 1 && xc[0] >= 5 ||
rm === 2 && (xc[0] > 5 || xc[0] === 5 && (more || xc[1] !== UNDEFINED))
);
xc.length = 1;
if (more) {
// 1, 0.1, 0.01, 0.001, 0.0001 etc.
x.e = x.e - sd + 1;
xc[0] = 1;
} else {
// Zero.
xc[0] = x.e = 0;
}
} else if (sd < xc.length) {
// xc[sd] is the digit after the digit that may be rounded up.
more =
rm === 1 && xc[sd] >= 5 ||
rm === 2 && (xc[sd] > 5 || xc[sd] === 5 &&
(more || xc[sd + 1] !== UNDEFINED || xc[sd - 1] & 1)) ||
rm === 3 && (more || !!xc[0]);
// Remove any digits after the required precision.
xc.length = sd;
// Round up?
if (more) {
// Rounding up may mean the previous digit has to be rounded up.
for (; ++xc[--sd] > 9;) {
xc[sd] = 0;
if (sd === 0) {
++x.e;
xc.unshift(1);
break;
}
}
}
// Remove trailing zeros.
for (sd = xc.length; !xc[--sd];) xc.pop();
}
return x;
}
/*
* Return a string representing the value of Big x in normal or exponential notation.
* Handles P.toExponential, P.toFixed, P.toJSON, P.toPrecision, P.toString and P.valueOf.
*/
function stringify(x, doExponential, isNonzero) {
var e = x.e,
s = x.c.join(''),
n = s.length;
// Exponential notation?
if (doExponential) {
s = s.charAt(0) + (n > 1 ? '.' + s.slice(1) : '') + (e < 0 ? 'e' : 'e+') + e;
// Normal notation.
} else if (e < 0) {
for (; ++e;) s = '0' + s;
s = '0.' + s;
} else if (e > 0) {
if (++e > n) {
for (e -= n; e--;) s += '0';
} else if (e < n) {
s = s.slice(0, e) + '.' + s.slice(e);
}
} else if (n > 1) {
s = s.charAt(0) + '.' + s.slice(1);
}
return x.s < 0 && isNonzero ? '-' + s : s;
}
// Prototype/instance methods
/*
* Return a new Big whose value is the absolute value of this Big.
*/
P.abs = function() {
var x = new this.constructor(this);
x.s = 1;
return x;
};
/*
* Return 1 if the value of this Big is greater than the value of Big y,
* -1 if the value of this Big is less than the value of Big y, or
* 0 if they have the same value.
*/
P.cmp = function(y) {
var isneg,
x = this,
xc = x.c,
yc = (y = new x.constructor(y)).c,
i = x.s,
j = y.s,
k = x.e,
l = y.e;
// Either zero?
if (!xc[0] || !yc[0]) return !xc[0] ? !yc[0] ? 0 : -j : i;
// Signs differ?
if (i != j) return i;
isneg = i < 0;
// Compare exponents.
if (k != l) return k > l ^ isneg ? 1 : -1;
j = (k = xc.length) < (l = yc.length) ? k : l;
// Compare digit by digit.
for (i = -1; ++i < j;) {
if (xc[i] != yc[i]) return xc[i] > yc[i] ^ isneg ? 1 : -1;
}
// Compare lengths.
return k == l ? 0 : k > l ^ isneg ? 1 : -1;
};
/*
* Return a new Big whose value is the value of this Big divided by the value of Big y, rounded,
* if necessary, to a maximum of Big.DP decimal places using rounding mode Big.RM.
*/
P.div = function(y) {
var x = this,
Big = x.constructor,
a = x.c, // dividend
b = (y = new Big(y)).c, // divisor
k = x.s == y.s ? 1 : -1,
dp = Big.DP;
if (dp !== ~~dp || dp < 0 || dp > MAX_DP) {
throw Error(INVALID_DP);
}
// Divisor is zero?
if (!b[0]) {
throw Error(DIV_BY_ZERO);
}
// Dividend is 0? Return +-0.
if (!a[0]) {
y.s = k;
y.c = [y.e = 0];
return y;
}
var bl, bt, n, cmp, ri,
bz = b.slice(),
ai = bl = b.length,
al = a.length,
r = a.slice(0, bl), // remainder
rl = r.length,
q = y, // quotient
qc = q.c = [],
qi = 0,
p = dp + (q.e = x.e - y.e) + 1; // precision of the result
q.s = k;
k = p < 0 ? 0 : p;
// Create version of divisor with leading zero.
bz.unshift(0);
// Add zeros to make remainder as long as divisor.
for (; rl++ < bl;) r.push(0);
do {
// n is how many times the divisor goes into current remainder.
for (n = 0; n < 10; n++) {
// Compare divisor and remainder.
if (bl != (rl = r.length)) {
cmp = bl > rl ? 1 : -1;
} else {
for (ri = -1, cmp = 0; ++ri < bl;) {
if (b[ri] != r[ri]) {
cmp = b[ri] > r[ri] ? 1 : -1;
break;
}
}
}
// If divisor < remainder, subtract divisor from remainder.
if (cmp < 0) {
// Remainder can't be more than 1 digit longer than divisor.
// Equalise lengths using divisor with extra leading zero?
for (bt = rl == bl ? b : bz; rl;) {
if (r[--rl] < bt[rl]) {
ri = rl;
for (; ri && !r[--ri];) r[ri] = 9;
--r[ri];
r[rl] += 10;
}
r[rl] -= bt[rl];
}
for (; !r[0];) r.shift();
} else {
break;
}
}
// Add the digit n to the result array.
qc[qi++] = cmp ? n : ++n;
// Update the remainder.
if (r[0] && cmp) r[rl] = a[ai] || 0;
else r = [a[ai]];
} while ((ai++ < al || r[0] !== UNDEFINED) && k--);
// Leading zero? Do not remove if result is simply zero (qi == 1).
if (!qc[0] && qi != 1) {
// There can't be more than one zero.
qc.shift();
q.e--;
p--;
}
// Round?
if (qi > p) round(q, p, Big.RM, r[0] !== UNDEFINED);
return q;
};
/*
* Return true if the value of this Big is equal to the value of Big y, otherwise return false.
*/
P.eq = function(y) {
return this.cmp(y) === 0;
};
/*
* Return true if the value of this Big is greater than the value of Big y, otherwise return
* false.
*/
P.gt = function(y) {
return this.cmp(y) > 0;
};
/*
* Return true if the value of this Big is greater than or equal to the value of Big y, otherwise
* return false.
*/
P.gte = function(y) {
return this.cmp(y) > -1;
};
/*
* Return true if the value of this Big is less than the value of Big y, otherwise return false.
*/
P.lt = function(y) {
return this.cmp(y) < 0;
};
/*
* Return true if the value of this Big is less than or equal to the value of Big y, otherwise
* return false.
*/
P.lte = function(y) {
return this.cmp(y) < 1;
};
/*
* Return a new Big whose value is the value of this Big minus the value of Big y.
*/
P.minus = P.sub = function(y) {
var i, j, t, xlty,
x = this,
Big = x.constructor,
a = x.s,
b = (y = new Big(y)).s;
// Signs differ?
if (a != b) {
y.s = -b;
return x.plus(y);
}
var xc = x.c.slice(),
xe = x.e,
yc = y.c,
ye = y.e;
// Either zero?
if (!xc[0] || !yc[0]) {
if (yc[0]) {
y.s = -b;
} else if (xc[0]) {
y = new Big(x);
} else {
y.s = 1;
}
return y;
}
// Determine which is the bigger number. Prepend zeros to equalise exponents.
if (a = xe - ye) {
if (xlty = a < 0) {
a = -a;
t = xc;
} else {
ye = xe;
t = yc;
}
t.reverse();
for (b = a; b--;) t.push(0);
t.reverse();
} else {
// Exponents equal. Check digit by digit.
j = ((xlty = xc.length < yc.length) ? xc : yc).length;
for (a = b = 0; b < j; b++) {
if (xc[b] != yc[b]) {
xlty = xc[b] < yc[b];
break;
}
}
}
// x < y? Point xc to the array of the bigger number.
if (xlty) {
t = xc;
xc = yc;
yc = t;
y.s = -y.s;
}
/*
* Append zeros to xc if shorter. No need to add zeros to yc if shorter as subtraction only
* needs to start at yc.length.
*/
if ((b = (j = yc.length) - (i = xc.length)) > 0)
for (; b--;) xc[i++] = 0;
// Subtract yc from xc.
for (b = i; j > a;) {
if (xc[--j] < yc[j]) {
for (i = j; i && !xc[--i];) xc[i] = 9;
--xc[i];
xc[j] += 10;
}
xc[j] -= yc[j];
}
// Remove trailing zeros.
for (; xc[--b] === 0;) xc.pop();
// Remove leading zeros and adjust exponent accordingly.
for (; xc[0] === 0;) {
xc.shift();
--ye;
}
if (!xc[0]) {
// n - n = +0
y.s = 1;
// Result must be zero.
xc = [ye = 0];
}
y.c = xc;
y.e = ye;
return y;
};
/*
* Return a new Big whose value is the value of this Big modulo the value of Big y.
*/
P.mod = function(y) {
var ygtx,
x = this,
Big = x.constructor,
a = x.s,
b = (y = new Big(y)).s;
if (!y.c[0]) {
throw Error(DIV_BY_ZERO);
}
x.s = y.s = 1;
ygtx = y.cmp(x) == 1;
x.s = a;
y.s = b;
if (ygtx) return new Big(x);
a = Big.DP;
b = Big.RM;
Big.DP = Big.RM = 0;
x = x.div(y);
Big.DP = a;
Big.RM = b;
return this.minus(x.times(y));
};
/*
* Return a new Big whose value is the value of this Big negated.
*/
P.neg = function() {
var x = new this.constructor(this);
x.s = -x.s;
return x;
};
/*
* Return a new Big whose value is the value of this Big plus the value of Big y.
*/
P.plus = P.add = function(y) {
var e, k, t,
x = this,
Big = x.constructor;
y = new Big(y);
// Signs differ?
if (x.s != y.s) {
y.s = -y.s;
return x.minus(y);
}
var xe = x.e,
xc = x.c,
ye = y.e,
yc = y.c;
// Either zero?
if (!xc[0] || !yc[0]) {
if (!yc[0]) {
if (xc[0]) {
y = new Big(x);
} else {
y.s = x.s;
}
}
return y;
}
xc = xc.slice();
// Prepend zeros to equalise exponents.
// Note: reverse faster than unshifts.
if (e = xe - ye) {
if (e > 0) {
ye = xe;
t = yc;
} else {
e = -e;
t = xc;
}
t.reverse();
for (; e--;) t.push(0);
t.reverse();
}
// Point xc to the longer array.
if (xc.length - yc.length < 0) {
t = yc;
yc = xc;
xc = t;
}
e = yc.length;
// Only start adding at yc.length - 1 as the further digits of xc can be left as they are.
for (k = 0; e; xc[e] %= 10) k = (xc[--e] = xc[e] + yc[e] + k) / 10 | 0;
// No need to check for zero, as +x + +y != 0 && -x + -y != 0
if (k) {
xc.unshift(k);
++ye;
}
// Remove trailing zeros.
for (e = xc.length; xc[--e] === 0;) xc.pop();
y.c = xc;
y.e = ye;
return y;
};
/*
* Return a Big whose value is the value of this Big raised to the power n.
* If n is negative, round to a maximum of Big.DP decimal places using rounding
* mode Big.RM.
*
* n {number} Integer, -MAX_POWER to MAX_POWER inclusive.
*/
P.pow = function(n) {
var x = this,
one = new x.constructor('1'),
y = one,
isneg = n < 0;
if (n !== ~~n || n < -MAX_POWER || n > MAX_POWER) {
throw Error(INVALID + 'exponent');
}
if (isneg) n = -n;
for (;;) {
if (n & 1) y = y.times(x);
n >>= 1;
if (!n) break;
x = x.times(x);
}
return isneg ? one.div(y) : y;
};
/*
* Return a new Big whose value is the value of this Big rounded to a maximum precision of sd
* significant digits using rounding mode rm, or Big.RM if rm is not specified.
*
* sd {number} Significant digits: integer, 1 to MAX_DP inclusive.
* rm? {number} Rounding mode: 0 (down), 1 (half-up), 2 (half-even) or 3 (up).
*/
P.prec = function(sd, rm) {
if (sd !== ~~sd || sd < 1 || sd > MAX_DP) {
throw Error(INVALID + 'precision');
}
return round(new this.constructor(this), sd, rm);
};
/*
* Return a new Big whose value is the value of this Big rounded to a maximum of dp decimal places
* using rounding mode rm, or Big.RM if rm is not specified.
* If dp is negative, round to an integer which is a multiple of 10**-dp.
* If dp is not specified, round to 0 decimal places.
*
* dp? {number} Integer, -MAX_DP to MAX_DP inclusive.
* rm? {number} Rounding mode: 0 (down), 1 (half-up), 2 (half-even) or 3 (up).
*/
P.round = function(dp, rm) {
if (dp === UNDEFINED) dp = 0;
else if (dp !== ~~dp || dp < -MAX_DP || dp > MAX_DP) {
throw Error(INVALID_DP);
}
return round(new this.constructor(this), dp + this.e + 1, rm);
};
/*
* Return a new Big whose value is the square root of the value of this Big, rounded, if
* necessary, to a maximum of Big.DP decimal places using rounding mode Big.RM.
*/
P.sqrt = function() {
var r, c, t,
x = this,
Big = x.constructor,
s = x.s,
e = x.e,
half = new Big('0.5');
// Zero?
if (!x.c[0]) return new Big(x);
// Negative?
if (s < 0) {
throw Error(NAME + 'No square root');
}
// Estimate.
s = Math.sqrt(x + '');
// Math.sqrt underflow/overflow?
// Re-estimate: pass x coefficient to Math.sqrt as integer, then adjust the result exponent.
if (s === 0 || s === 1 / 0) {
c = x.c.join('');
if (!(c.length + e & 1)) c += '0';
s = Math.sqrt(c);
e = ((e + 1) / 2 | 0) - (e < 0 || e & 1);
r = new Big((s == 1 / 0 ? '5e' : (s = s.toExponential()).slice(0, s.indexOf('e') + 1)) + e);
} else {
r = new Big(s + '');
}
e = r.e + (Big.DP += 4);
// Newton-Raphson iteration.
do {
t = r;
r = half.times(t.plus(x.div(t)));
} while (t.c.slice(0, e).join('') !== r.c.slice(0, e).join(''));
return round(r, (Big.DP -= 4) + r.e + 1, Big.RM);
};
/*
* Return a new Big whose value is the value of this Big times the value of Big y.
*/
P.times = P.mul = function(y) {
var c,
x = this,
Big = x.constructor,
xc = x.c,
yc = (y = new Big(y)).c,
a = xc.length,
b = yc.length,
i = x.e,
j = y.e;
// Determine sign of result.
y.s = x.s == y.s ? 1 : -1;
// Return signed 0 if either 0.
if (!xc[0] || !yc[0]) {
y.c = [y.e = 0];
return y;
}
// Initialise exponent of result as x.e + y.e.
y.e = i + j;
// If array xc has fewer digits than yc, swap xc and yc, and lengths.
if (a < b) {
c = xc;
xc = yc;
yc = c;
j = a;
a = b;
b = j;
}
// Initialise coefficient array of result with zeros.
for (c = new Array(j = a + b); j--;) c[j] = 0;
// Multiply.
// i is initially xc.length.
for (i = b; i--;) {
b = 0;
// a is yc.length.
for (j = a + i; j > i;) {
// Current sum of products at this digit position, plus carry.
b = c[j] + yc[i] * xc[j - i - 1] + b;
c[j--] = b % 10;
// carry
b = b / 10 | 0;
}
c[j] = b;
}
// Increment result exponent if there is a final carry, otherwise remove leading zero.
if (b) ++y.e;
else c.shift();
// Remove trailing zeros.
for (i = c.length; !c[--i];) c.pop();
y.c = c;
return y;
};
/*
* Return a string representing the value of this Big in exponential notation rounded to dp fixed
* decimal places using rounding mode rm, or Big.RM if rm is not specified.
*
* dp? {number} Decimal places: integer, 0 to MAX_DP inclusive.
* rm? {number} Rounding mode: 0 (down), 1 (half-up), 2 (half-even) or 3 (up).
*/
P.toExponential = function(dp, rm) {
var x = this,
n = x.c[0];
if (dp !== UNDEFINED) {
if (dp !== ~~dp || dp < 0 || dp > MAX_DP) {
throw Error(INVALID_DP);
}
x = round(new x.constructor(x), ++dp, rm);
for (; x.c.length < dp;) x.c.push(0);
}
return stringify(x, true, !!n);
};
/*
* Return a string representing the value of this Big in normal notation rounded to dp fixed
* decimal places using rounding mode rm, or Big.RM if rm is not specified.
*
* dp? {number} Decimal places: integer, 0 to MAX_DP inclusive.
* rm? {number} Rounding mode: 0 (down), 1 (half-up), 2 (half-even) or 3 (up).
*
* (-0).toFixed(0) is '0', but (-0.1).toFixed(0) is '-0'.
* (-0).toFixed(1) is '0.0', but (-0.01).toFixed(1) is '-0.0'.
*/
P.toFixed = function(dp, rm) {
var x = this,
n = x.c[0];
if (dp !== UNDEFINED) {
if (dp !== ~~dp || dp < 0 || dp > MAX_DP) {
throw Error(INVALID_DP);
}
x = round(new x.constructor(x), dp + x.e + 1, rm);
// x.e may have changed if the value is rounded up.
for (dp = dp + x.e + 1; x.c.length < dp;) x.c.push(0);
}
return stringify(x, false, !!n);
};
/*
* Return a string representing the value of this Big.
* Return exponential notation if this Big has a positive exponent equal to or greater than
* Big.PE, or a negative exponent equal to or less than Big.NE.
* Omit the sign for negative zero.
*/
P.toJSON = P.toString = function() {
var x = this,
Big = x.constructor;
return stringify(x, x.e <= Big.NE || x.e >= Big.PE, !!x.c[0]);
};
/*
* Return the value of this Big as a primitve number.
*/
P.toNumber = function() {
var n = Number(stringify(this, true, true));
if (this.constructor.strict === true && !this.eq(n.toString())) {
throw Error(NAME + 'Imprecise conversion');
}
return n;
};
/*
* Return a string representing the value of this Big rounded to sd significant digits using
* rounding mode rm, or Big.RM if rm is not specified.
* Use exponential notation if sd is less than the number of digits necessary to represent
* the integer part of the value in normal notation.
*
* sd {number} Significant digits: integer, 1 to MAX_DP inclusive.
* rm? {number} Rounding mode: 0 (down), 1 (half-up), 2 (half-even) or 3 (up).
*/
P.toPrecision = function(sd, rm) {
var x = this,
Big = x.constructor,
n = x.c[0];
if (sd !== UNDEFINED) {
if (sd !== ~~sd || sd < 1 || sd > MAX_DP) {
throw Error(INVALID + 'precision');
}
x = round(new Big(x), sd, rm);
for (; x.c.length < sd;) x.c.push(0);
}
return stringify(x, sd <= x.e || x.e <= Big.NE || x.e >= Big.PE, !!n);
};
/*
* Return a string representing the value of this Big.
* Return exponential notation if this Big has a positive exponent equal to or greater than
* Big.PE, or a negative exponent equal to or less than Big.NE.
* Include the sign for negative zero.
*/
P.valueOf = function() {
var x = this,
Big = x.constructor;
if (Big.strict === true) {
throw Error(NAME + 'valueOf disallowed');
}
return stringify(x, x.e <= Big.NE || x.e >= Big.PE, true);
};
// Export
Big = _Big_();
export default Big;
数字其他
数字补0
/**
* @description 日期的月或日补零操作
* @param {String} value 需要补零的值
*/
function padZero(value) {
if (typeof value == "undefined") {
value = ""
}
return ('00' + value).slice(-2);
}
console.log("空补零", padZero()) //00
console.log("0补零", padZero(0)) //00
console.log("2补零", padZero(1)) //01
阿拉伯数字转汉字
var number = 323413290907;
function convertToChinese(num, last) {
var N = ['零', '一', '二', '三', '四', '五', '六', '七', '八', '九'];
var str = num.toString();
var len = num.toString().length;
var C_Num = [];
for (var i = 0; i < len; i++) {
C_Num.push(N[str.charAt(i)]);
}
//console.log("C_Num.", C_Num)
if (last) {
return C_Num[C_Num.length - 1]
}
return C_Num.join('');
}
console.log("323413290907 =>", convertToChinese(number)) //323413290907 => 三二三四一三二九零九零七


 浙公网安备 33010602011771号
浙公网安备 33010602011771号