密码算法逆向分析思路
MD5
明文分组64字节
4个初始化向量,输出结果16字节
a 0x67452301
b 0xEFCDAB89
c 0x98BADCFE
d 0x10325476
update明文超过一个分组时,进行MD5Transform,直到明文不足一个分组
final结果时,填充80字节和若干00字节,至少填充一个80字节,至多填充80和00共计64个字节,最后8字节填充明文真实位长度(明文以字节为单位)
核心MD5Transform
64轮迭代
首先要对明文分组进行分块,并进行端序转换
由于MD5是小端序的,如果系统是大端序的,明文分块时需要进行段序转换;如果系统是小端序的,明文分块时则不需要进行段序转换
每16轮用一个逻辑函数
如函数 FF(a, b, c, d, x[0], 7, 0xd76aa478); /* 1 */
实现为
#define FF(a,b,c,d,x,s,ac) \
{ \
a += F(b,c,d) + x + ac; \
a = ROTATE_LEFT(a,s); \
a += b; \
}
要进行的操作有,对bcd进行位运算,加上明文分块,加上k,再加上a本身
接着循环移位
最后在加b
上面的过程只修改了a
完毕后
a = d
b = a
c = b
d = c
进行下一轮的同样的操作
每16轮更换一次逻辑函数,共有4个逻辑函数
每一轮用到一个k值,有64个k值
循环移位的位数4轮一个小周期,16轮一个大周期
前16轮用到的明文按序排列
后48轮用变为随机化序列,但每4轮里的分块间隔是一致的
轮函数结束后,context里的向量值+= a,b,c,d
最后输出时,再进行一次端序转换
总结就是int* 到 char*或者反过来,都要进行端序转换
SHA1
同为消息摘要算法
有5个初始化向量,输出为20个字节
a 0x67452301
b 0xEFCDAB89
c 0x98BADCFE
d 0x10325476
e 0xC3D2E1F0
sha1算法进行80轮迭代,每一轮按序用到一个明文分块
sha1算法是大端字节序,明文分块时需要进行端序转换
随后,由于分组长度只有64字节,得到16个分块,需要对明文分块进行拓展,拓展至80个分块
拓展算法
for (t = 16; t < 80; t++) {
W[t] = SHA1CircularShift(1, W[t - 3] ^ W[t - 8] ^ W[t - 14] ^ W[t - 16]);
}
位异或后需要循环左移一位,否则就是sha0算法了
拓展后,进行80轮的迭代,每20轮用到一个k值,总共4个k值
for (t = 0; t < 20; t++) {
temp = SHA1CircularShift(5, A) +
((B & C) | ((~B) & D)) + E + W[t] + K[0];
E = D;
D = C;
C = SHA1CircularShift(30, B);
B = A;
A = temp;
}
同样可以理解为只对A进行运算,最后平移,C较为特殊,先对B做一个循环左移再赋值
A的运算:先对A循环移位,加对BCD做位运算的结果,再加E,再加明文分块,再加k
轮函数结束后,context里的向量值+= a,b,c,d,e
SHA256
64字节的明文分组
8个初始化向量,输出为32字节
A 0x6a09e667
B 0xbb67ae85
C 0x3c6ef372
D 0xa54ff53a
E 0x510e527f
F 0x9b05688c
G 0x1f83d9ab
H 0x5be0cd19
进行64轮迭代,每轮迭代按序用到一个明文分块
明文分块且端序转换后,进行分块拓展,拓展至64个分块
for ( ; i < 64; ++i)
m[i] = SIG1(m[i - 2]) + m[i - 7] + SIG0(m[i - 15]) + m[i - 16];
#define SIG0(x) (ROTRIGHT(x,7) ^ ROTRIGHT(x,18) ^ ((x) >> 3))
#define SIG1(x) (ROTRIGHT(x,17) ^ ROTRIGHT(x,19) ^ ((x) >> 10))
每轮迭代用到一个k值,共有64个k值
for (i = 0; i < 64; ++i) {
t1 = h + EP1(e) + CH(e,f,g) + k[i] + m[i];
t2 = EP0(a) + MAJ(a,b,c);
h = g;
g = f;
f = e;
e = d + t1;
d = c;
c = b;
b = a;
a = t1 + t2;
}
只对a修改,其它平移,e较为特殊
#define CH(x,y,z) (((x) & (y)) ^ (~(x) & (z)))
#define MAJ(x,y,z) (((x) & (y)) ^ ((x) & (z)) ^ ((y) & (z)))
#define EP0(x) (ROTRIGHT(x,2) ^ ROTRIGHT(x,13) ^ ROTRIGHT(x,22))
#define EP1(x) (ROTRIGHT(x,6) ^ ROTRIGHT(x,11) ^ ROTRIGHT(x,25))
轮函数结束后,context里的向量值+= a,b,c,d,e,f,g,h
SHA512
明文分组128字节,分块大小为8字节
有8个初始化向量,输出为64个字节
进行80轮迭代,每轮用到一个明文分块,一个k值
需要进行明文分块拓展,拓展至80块
for (i = 16; i < 80; i++) {
W[i] = Gamma1(W[i - 2]) + W[i - 7] + Gamma0(W[i - 15]) + W[i - 16];
}
#define Sha512Round(a, b, c, d, e, f, g, h, i) \
t0 = h + Sigma1(e) + Ch(e, f, g) + K[i] + W[i]; \
t1 = Sigma0(a) + Maj(a, b, c); \
d += t0; \
h = t0 + t1;
轮函数只修改d和h,下一轮所有向量平移
DES
第1步:子密钥的生成
根据pc1表对密钥进行重排列,重排列后由64位变成56位,每个字节的最后一位被去除(PC1_Table[56])
将密钥分为左右两半,C0和D0
将C0和D0进行循环移位,得到C1和D1
key_shift = [1, 1, 2, 2, 2, 2, 2, 2, 1, 2, 2, 2, 2, 2, 2, 1];
最终得到C1,D1到C16,D16
将C和D合并,根据pc2表进行重排列,得到子密钥K1到K16(PC2_Table[48])
重排列后由56位变成48位
第2步:明文的编排
根据ip表对明文进行初始置换,每个明文分组64位(IP_Table[64])
第3步:明文的运算
将编排后的明文分成左右两半,L0和R0
16轮迭代的基本套路
Ln = Rn-1
Rn = Ln-1 ^ f(Rn-1, Kn)
在f(Rn-1, Kn)中
首先将Rn-1与Kn异或
由于Rn-1为32位,Kn为48位,需要先对Rn-1进行位拓展,使用到E表(E_Table[48])
DES算法核心
接着,将异或的结果分成8块,每块6bit
查S盒进行代换(int S_Box[8][4][16])
最后8个6比特的值在S盒作用下变成8个4比特的值
最后,得到的结果进行P表的重排(int P_Table[32])
f结束后,再与Ln-1异或,得到Rn
进行16轮,完毕后交换L16和R16,拼接(为了方便做逆运算,把整个16轮倒着看就理解了)
最后根据FP表进行末置换(FP_Table[64])
若只有初始置换和末置换是逆过程
AES
AES标准实现
ase的整体流程可分为明文的处理和密钥的编排
AES要进行一轮的密钥加和10轮的运算,每一轮用到一个密钥
密钥加用到主密钥,即原密钥。需要主密钥扩展出10个轮密钥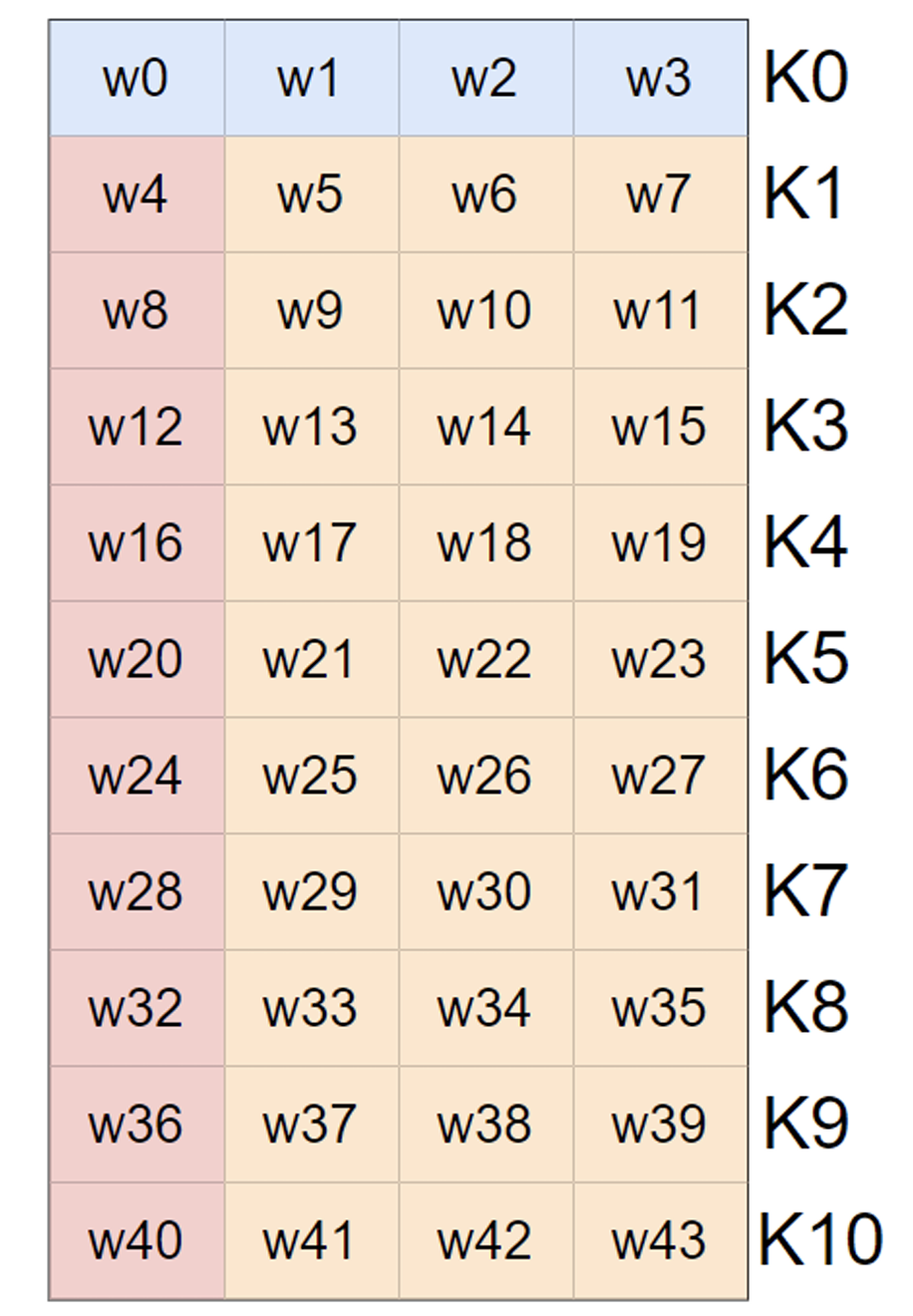
一个密钥分成4块
其中左侧红色部分的计算![]()
g函数一共三个步骤——循环左移、S盒替换、字节异或
1.循环左移
循环左移一个字节即可
2.S盒替换
将数值本身作为索引取出S数组中对用的值
3.字节异或
将上一步结果中的最高字节和一个固定常量异或
rcon = [0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36],共10个,每次计算按序用一个
其它部分的计算更为简单![]()
直接取前一个和头顶上的一个异或即可
已知任意一个轮密钥,可以推出其它轮密钥包括主密钥
例如,已知k10,即已知W40,W41,W42,W43
有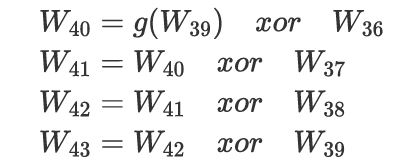
W40已知,g已知,W39可以通过W43与W42异或得到,W36也就得到了
据此可以依次推导出全部的轮密钥包括主密钥
密钥的编排结束,接着进行明文的处理
首先要调整明文的格式,对于aes-128,16字节的明文分组,调整为一个4x4的矩阵,从低字节开始,按列挨个填充。对kn进行同样的处理
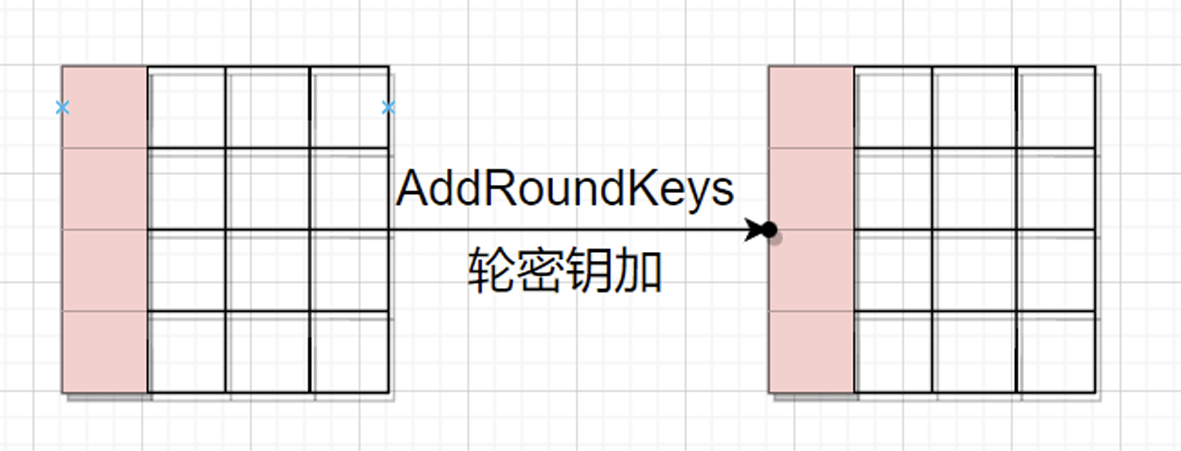
接着,初始轮密钥加,明文矩阵和K0异或(为什么不叫轮密钥异或而叫轮密钥加),得到state
接着是10轮主运算,有如下伪代码
前9轮与第10轮稍有不同
前九轮运算中,包含四个步骤:字节替换,行移位,列混淆,轮密钥加。
第十轮中,包含三个步骤:字节替换,行移位,轮密钥加。相比前九轮缺一个列混淆,其余相同。
1.字节替换
即S盒替换
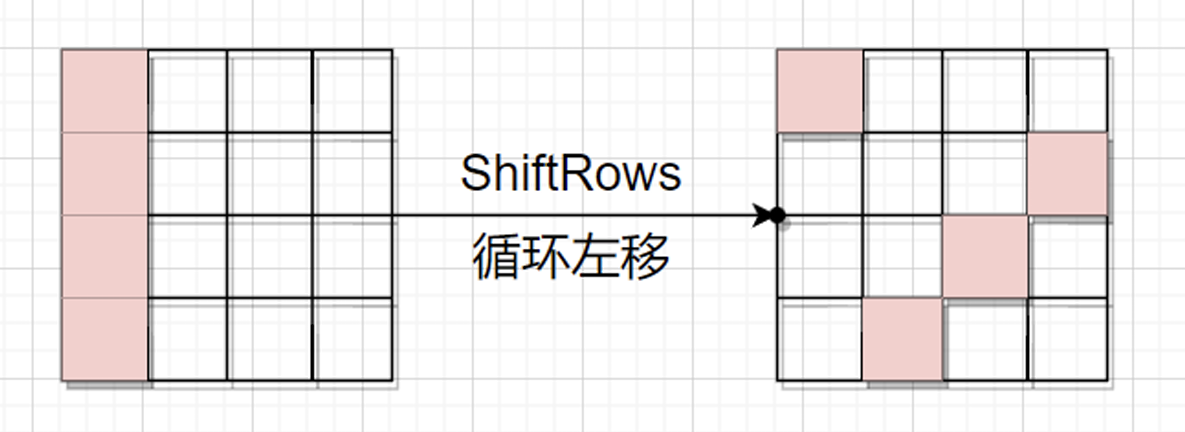
2.行移位
第一行不循环左移,第二行循环左移1字节,第三行循环左移2字节,第四行循环左移3字节。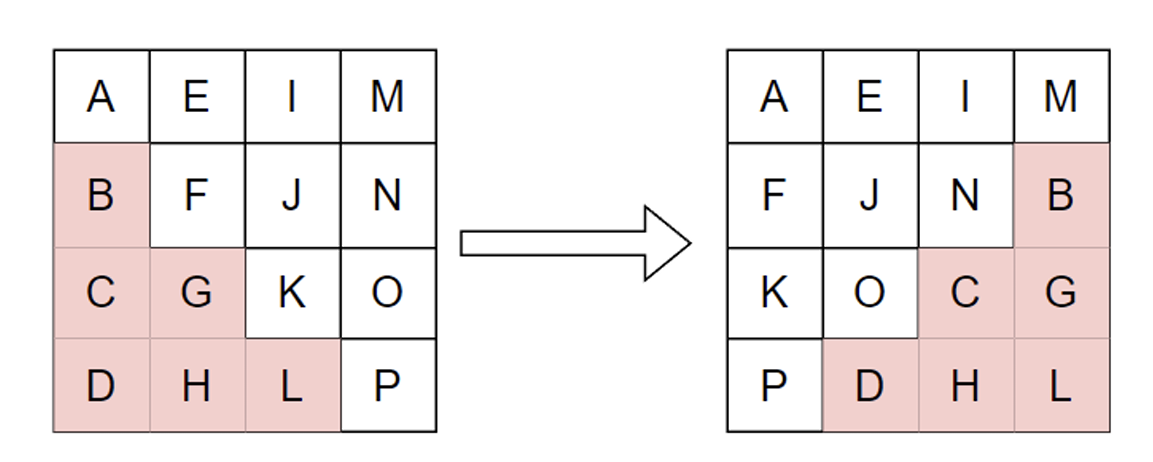
3.列混淆
state,左边乘如下所示固定矩阵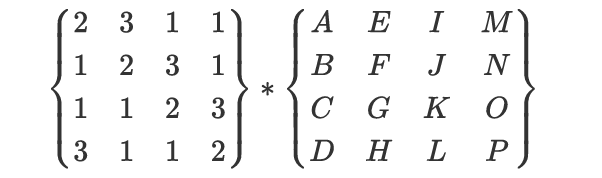

4.轮密钥加
同上,state矩阵异或上轮密钥矩阵
将state铺开就得到结果了
AES查表实现
为了加快加密速度,常使用查表法的aes,将1至9轮的字节替换,行移位,列混淆三个步骤合为一个查T表的步骤
一般的一轮加密过程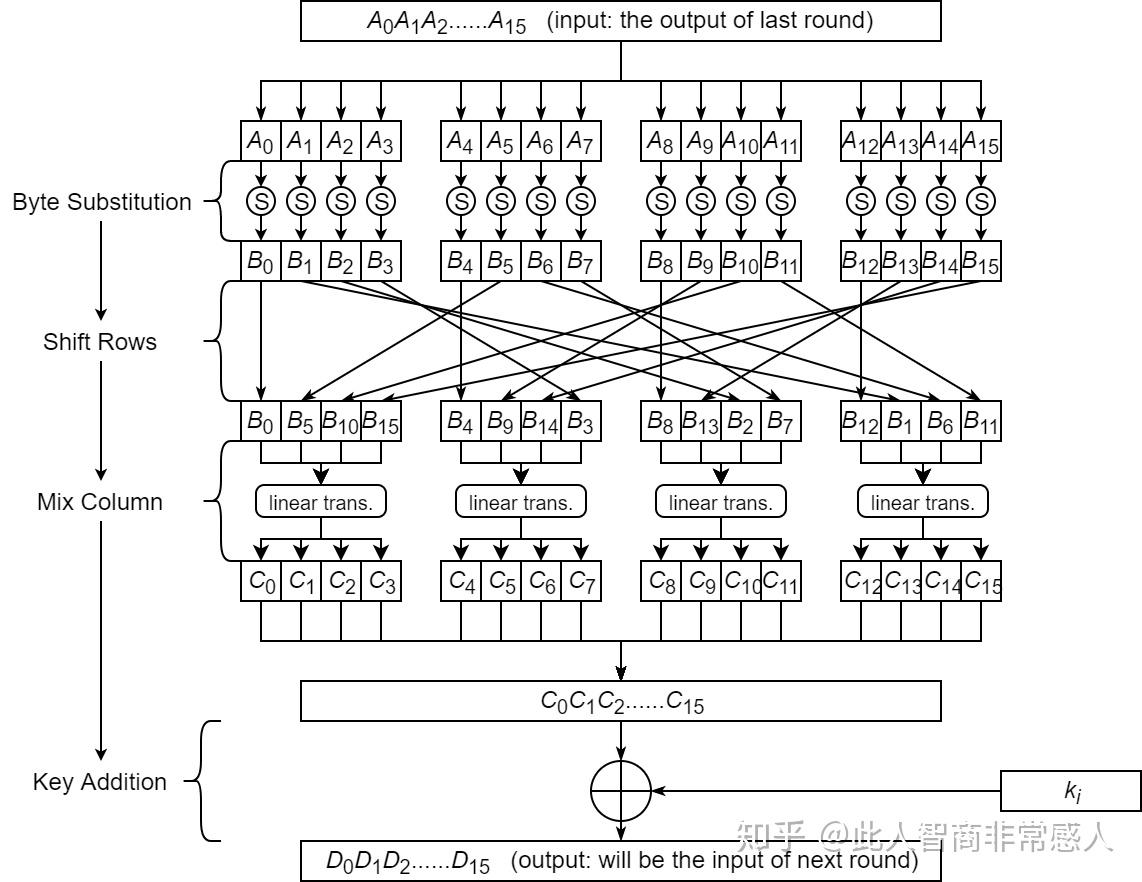
字节替换和行移位两个过程交换并不影响加密的结果,便有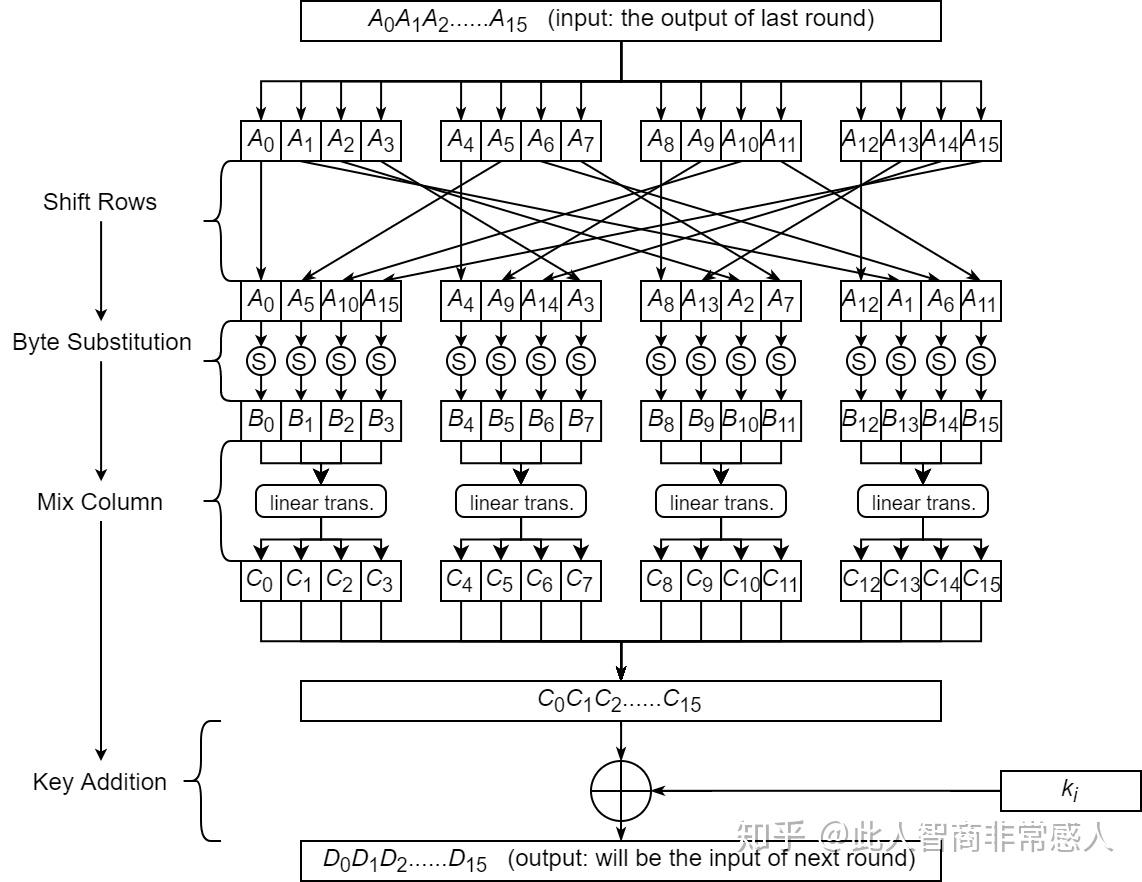
列混淆
只计算低4字节,即第一列,有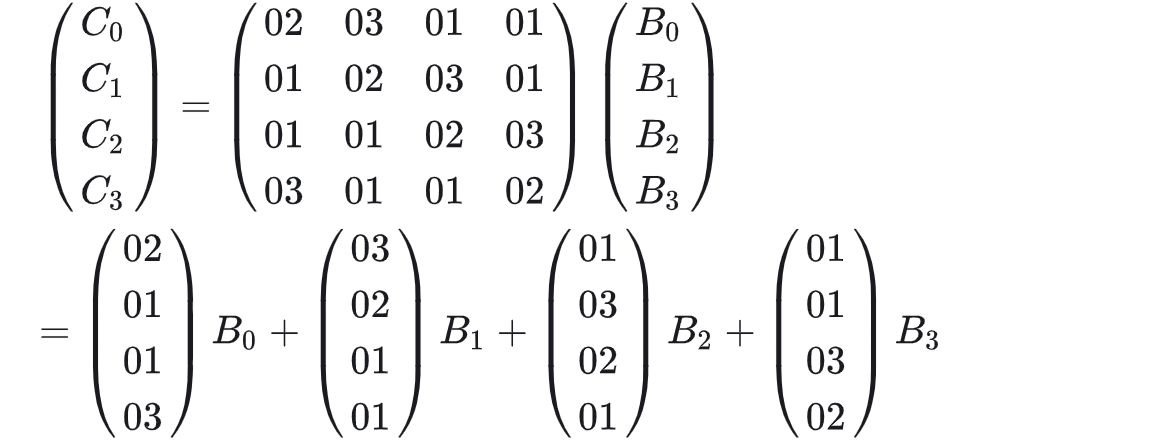
B是经过行移位后查S表得到的,有
对T盒做如下定义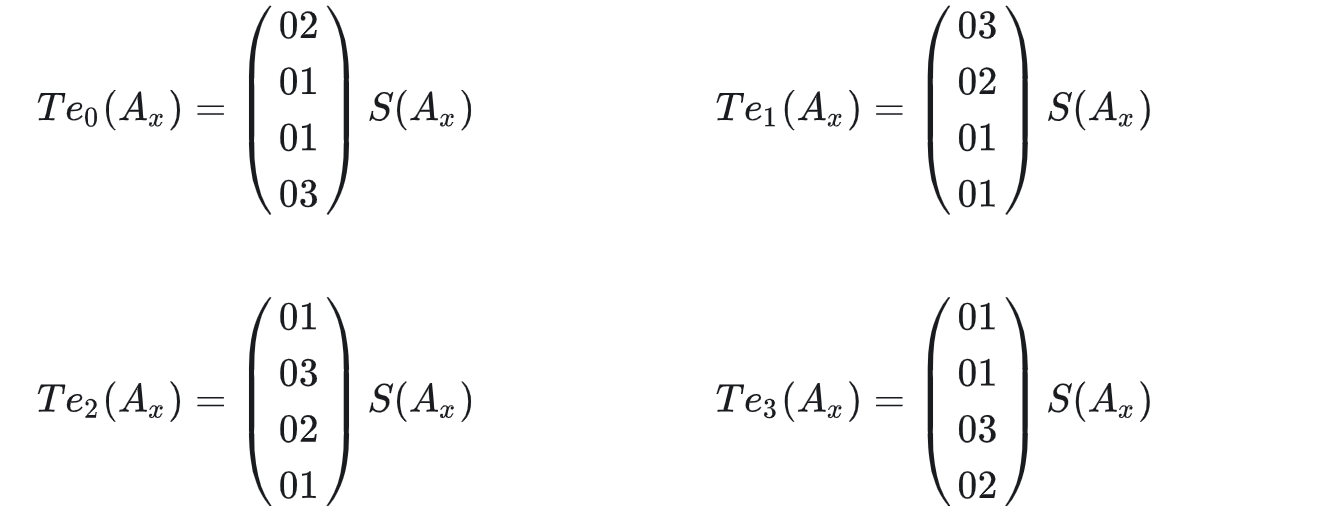
T盒元素数量对应S盒元素数量为256个,每个元素为4字节,这样间接的查S盒操作就变成了直接的查T表操作
轮操作就可以化为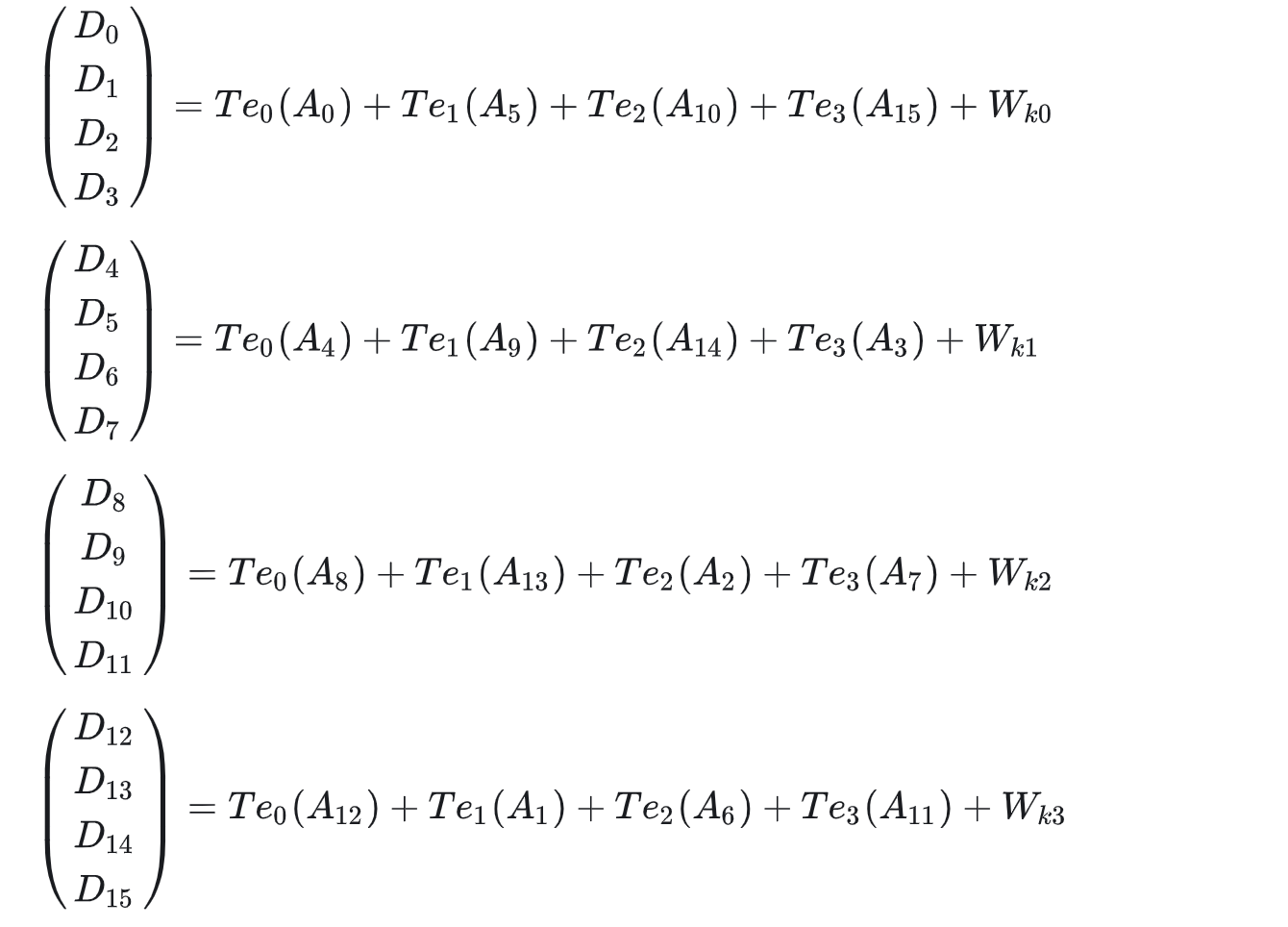
白盒AES
查表法将轮运算的前三步结合为一个查表步骤
白盒加密相当于在查表法的基础上进一步升级,将轮密钥加也和前三步合并,查一个新的,更大的表
密钥不需要进行拓展了,也根本不许要传入密钥,密钥已经融入到表里面去了,此时就很难拿到原始的密钥了
轮密钥可以推导出主密钥,如何获取轮密钥?
差分故障攻击
在对称加密算法中,扩散(Diffusion)和混淆(Confusion)是两个非常重要的安全原则。它们确保密文与明文或密钥之间的关系变得难以发现,从而增强安全性。
AES中实现混淆的主要步骤:
SubBytes(字节替换):
使用一个非线性的S-box,将每个字节进行非线性变换。这个步骤是AES中的核心混淆元素,因为它引入了复杂的非线性关系。
作用:提高非线性,使密文与密钥之间关系复杂化。
AES中实现扩散的主要步骤:
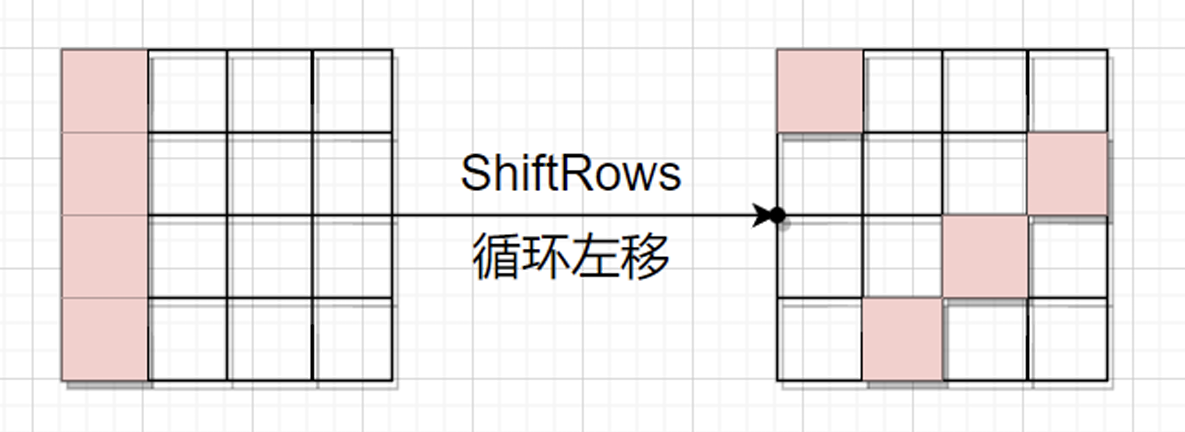
ShiftRows(行移位):
将状态矩阵中的字节进行循环移位,打乱字节的位置,增加不同字节之间的相互依赖。
作用:改变字节位置,扩散影响范围。
MixColumns(列混淆):
利用有限域上的线性变换,将每一列的字节混合,使得每个输出字节都受到一列中所有输入字节的影响。
作用:实现彻底的扩散,把每个字节的影响扩展到整列。
若只改变state的一个字节,
在经历下一次的列混淆之前,错误不会被扩散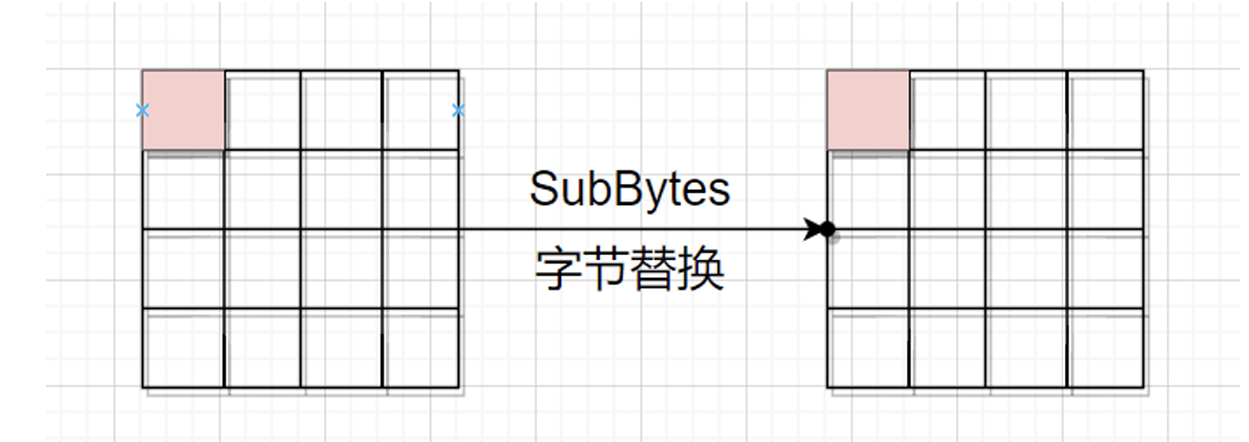
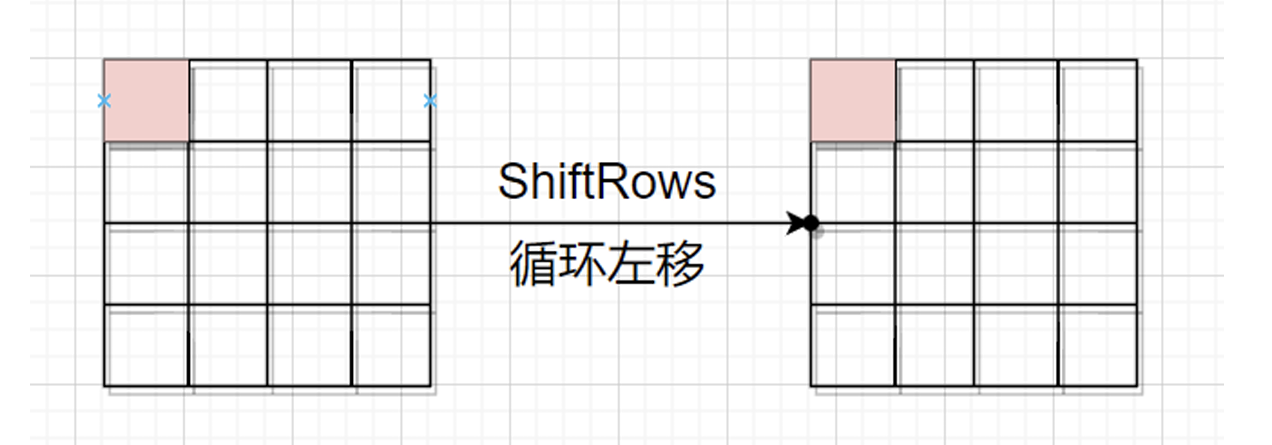
在经历一轮的列混淆之后,两轮的列混淆之前,错误会扩散到4个字节(因为进行了矩阵相乘)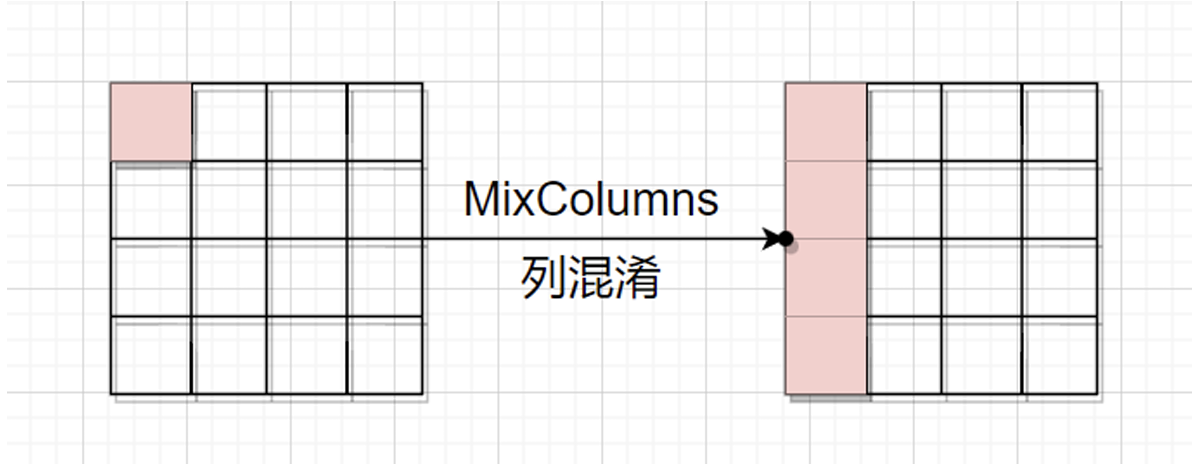
next 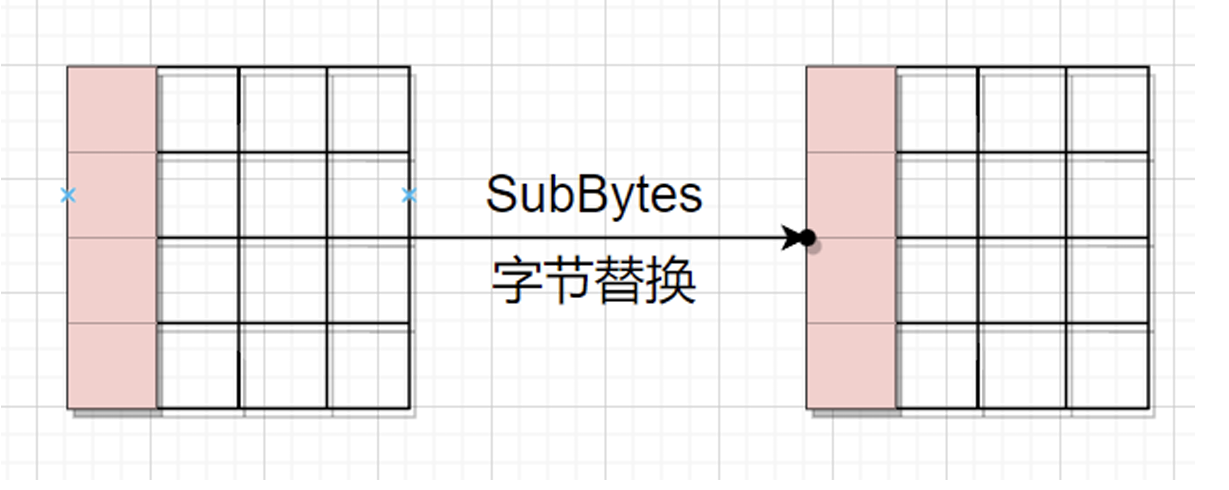
在进行第二轮的列混淆之后,错误扩散到所有字节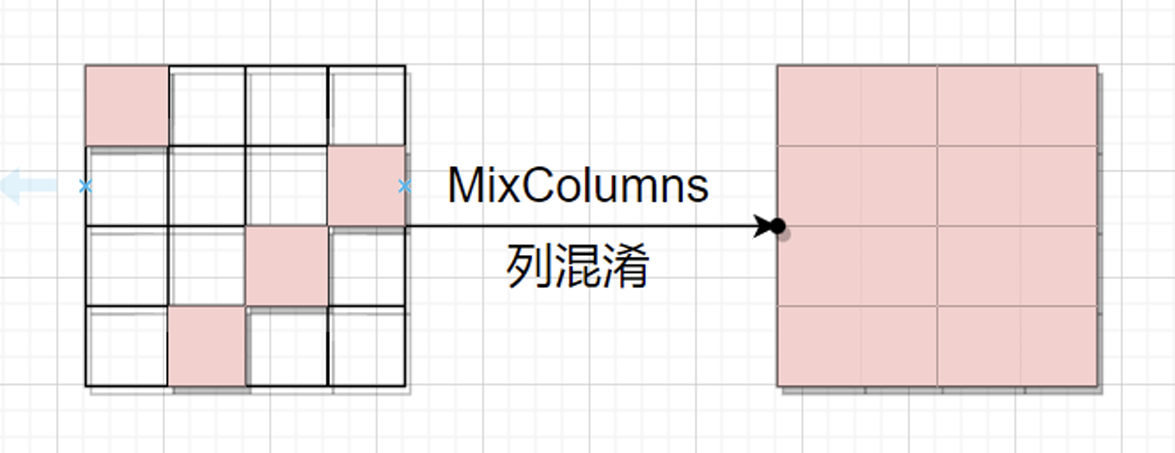
错误的一个字节出现在其它位同理,对应4种扩散情况
基于上述情况的分析,根据密文的状况,可以反推故障发生的地点
而推出故障发生的地点是为了进行差分攻击
差分攻击需要在以下时机实现
对于灰盒AES,我们能观测加密的结果,但观察不到state的中间量或故障导致的变化。因此正确密文和故障密文都可知,正确输入和故障输入都未知。
进而,输入差分未知,输出差分已知。式子左边已知,而右边的 以及输出差分 未知。
推导可得一个二元方程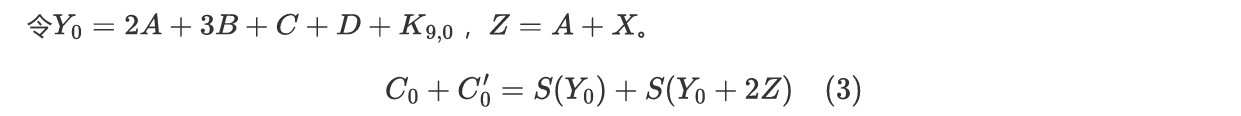
先不着急求Y0的解
对于任意的Y0,能够求出若干个Z的解
利用剩余的三个差分进一步约束Z的解集(4个差分的Z是相同的,解集取交集)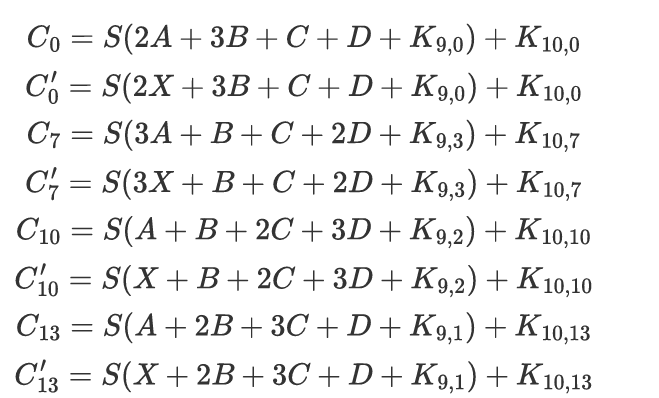
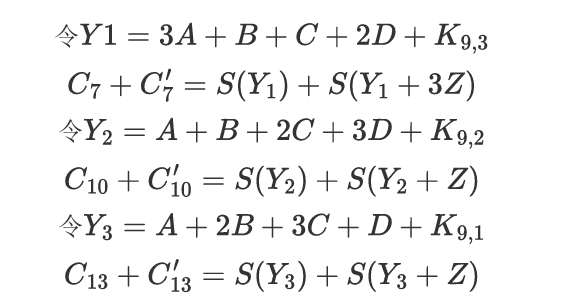
这样,得到的Z的解集,反过来可以求Y的解集,
又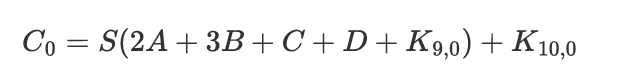
可以得到与Y解集数量相同的K10,0的解集
为了再进一步约束,只需重复实验,利用不同的差分得到不同的解集,最后取到只有一个元素的交集就算完成了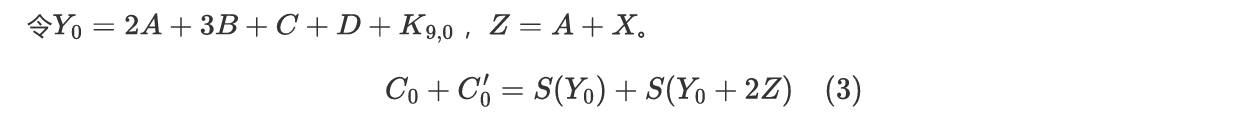
对于白盒AES而言,Z已知,便可推导出Y0,再结合![]()
可推导出K10,0 以及其它密钥字节
上面的计算有现成的算法,现在逆向的难点就来到了如何找到能够进行差分攻击的时机



 浙公网安备 33010602011771号
浙公网安备 33010602011771号