P9119 [春季测试 2023] 圣诞树

参考博客： 春季测试 2023] 圣诞树 题解 - 洛谷专栏 (luogu.com.cn)

题意：给定二维平面上一个凸多边形的 \(n\) 个顶点, 求一种方案，使得从最高点开始，不重复地经过所有点后距离的最小值。只要求输出这种方案。

经典的 TSP 问题。

\(n<=18\) 可以直接状压dp.

\(n<=1000\):

就是要大胆发现一些结论。

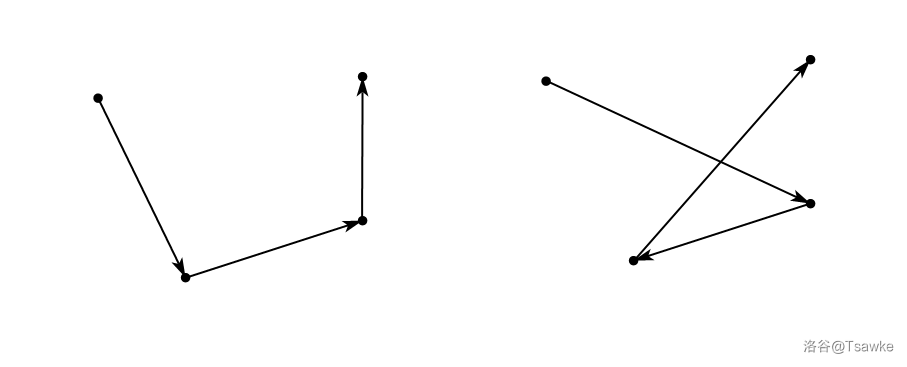
根据三角形法则，

对比图1和图2，发现如果电线交叉肯定不优。

所以对于逆时针给定的若干个点，当处于 \(𝑖\) 时，最优决策一定只能是下一步到 \(𝑖−1\) 或 \(i+1\)，否则将会存在一个点被隔离，导致最终去往该点时一定形成交叉路径。并且 \(i\) 之前的决策并不影响当前这一步的决策。

此时无后效性和子问题的雏形已经出现了，考虑动态规划。

• 定义：\(f[i][j][0/1]\), 区间\([i,j]\), 停在左边界/右边界， 最短距离
• 转移：

\[f[i][j][0] = \min(dis(i,i+1) + f[i+1][j][0] , dis(i,j) + f[i+1][j][1]) \]

\[f[i][j][1] = \min(dis(j-1,j) + f[i][j-1][1] , dis(i,j) + f[i][j-1][0]) \]

• 初始化：\(f[s][s][0/1] = 0\), 其他的初始化为 \(inf\)
• 扩展顺序：先从小到大枚举长度，再从左到右依次枚举所有区间
• 答案：由\(f[1][n][1]\) 往回倒推（最后一步仍然要遵循三角形法则，所以只考虑 \(f[1][n][1].\)）

#include<bits/stdc++.h>
#define F(i,l,r) for(int i(l);i<=(r);++i)
#define G(i,r,l) for(int i(r);i>=(l);--i)
#define int ll
using namespace std;
using ll = long long;
using ull = unsigned long long;
const int N=1e3+5;
const double inf = 1e18;
struct node{
	double x,y;
	int id;
}a[N],tmp[N];
double f[N][N][2];
int pre[N][N][2];
inline double dis(int i,int j){
	return sqrt((a[i].x-a[j].x) * (a[i].x-a[j].x) + (a[i].y-a[j].y) * (a[i].y-a[j].y));
}
int n,k=1;
inline void dfs(int i,int j,int op){
	if(i==j) return cout<<a[i].id,void();
	if(!op) cout<<a[i].id<<" ",dfs(i+1,j,pre[i][j][0]);
	else cout<<a[j].id<<" ", dfs(i,j-1,pre[i][j][1]);
	return  ;
}
signed main(){
//	freopen("tree.in","r",stdin); 
//	freopen("tree.out","w",stdout);
	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
	cin>>n; F(i,1,n) cin>>a[i].x>>a[i].y,a[i].id=i,tmp[i]=a[i];
	F(i,2,n) if(a[i].y>a[k].y) k=i;
	F(i,1,k) a[i+n-k]=tmp[i];
	F(i,k+1,n) a[i-k]=tmp[i];
	F(len,2,n-1){
		for(int i=1,j=len;j<=n;++i,++j){
			f[i][j][0] = f[i][j][1] = inf;
			if(dis(i,i+1) + f[i+1][j][0] < dis(i,j) + f[i+1][j][1]) 
				f[i][j][0] = dis(i,i+1) + f[i+1][j][0], pre[i][j][0] = 0;
			else 
				f[i][j][0] = dis(i,j) + f[i+1][j][1], pre[i][j][0] = 1;
			if(dis(j-1,j) + f[i][j-1][1] < dis(i,j) + f[i][j-1][0]) f[i][j][1] = dis(j-1,j) + f[i][j-1][1], pre[i][j][1] = 1;
			else  f[i][j][1] = dis(i,j) + f[i][j-1][0], pre[i][j][1] = 0; 
		}	
	}
	cout<<a[n].id<<" ";
	if(dis(n-1,n) + f[1][n-1][1] > dis(1,n) + f[1][n-1][0]) dfs(1,n-1,0);
	else dfs(1,n-1,1);
	return fflush(0),0;
}

总结一下，感觉拿到这道题还是没有冷静去分析条件，比如起点固定能不能利用？逆时针给定的这张图的顺序可能长什么样？不是从最高点开始给的图，我怎么通过一些简单的设计去调整？有哪些情况是显然不优的？敢不敢大胆排除？