06.数据结构与算法

这个上下午都考

大纲

0.数据结构的定义

就是计算机组织和存储数据的方式

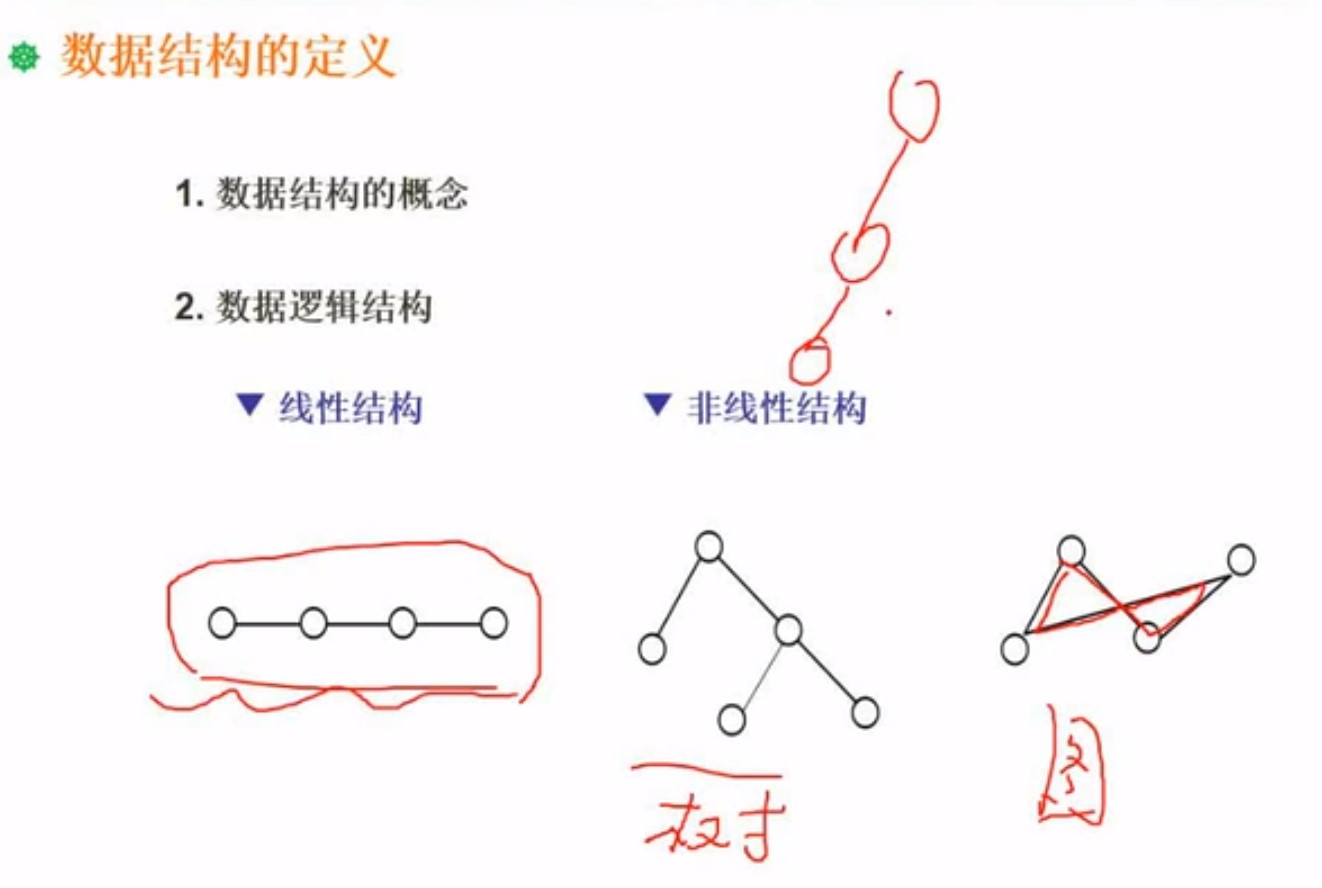
树没有环路，图可能存在环路

广义的图包括树和线性结构

广义的树包括线性结构

线性结构就是线

非线性结果普分为树和图

1.数组和矩阵

1.1.数组（重点）

数组要掌握的是存储地址的计算      计算偏移量

我们要看一个元素是多少个字节来判断，例如数组0个存储地址就是  a[0] = a

a[1] = a + 1*1(占用多少字节)，来计算存储地址  

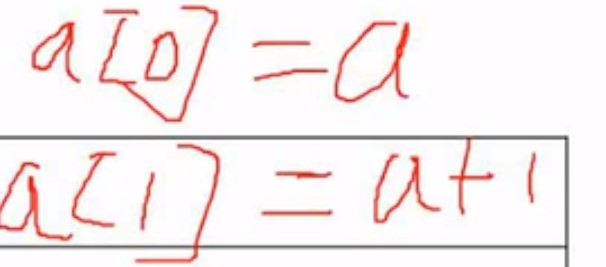
行是从0开始，列也是从0开始

二维数组的存储地址计算也一样，无论从行，还是按列存，第一个都是a[0][0] = a

接着除了第一个看到

例如55二位数组，按照行的a[2][3]

就是按照行列都是从0开始，除了a,一共还有13个格子

就是说地址是 a+字节长度*13 = 结果

这个a[i][j]   i是行，j是列

a[m][n]   m是有多少行(一列多少个格子)，n是有多少列(一行多少个格子)

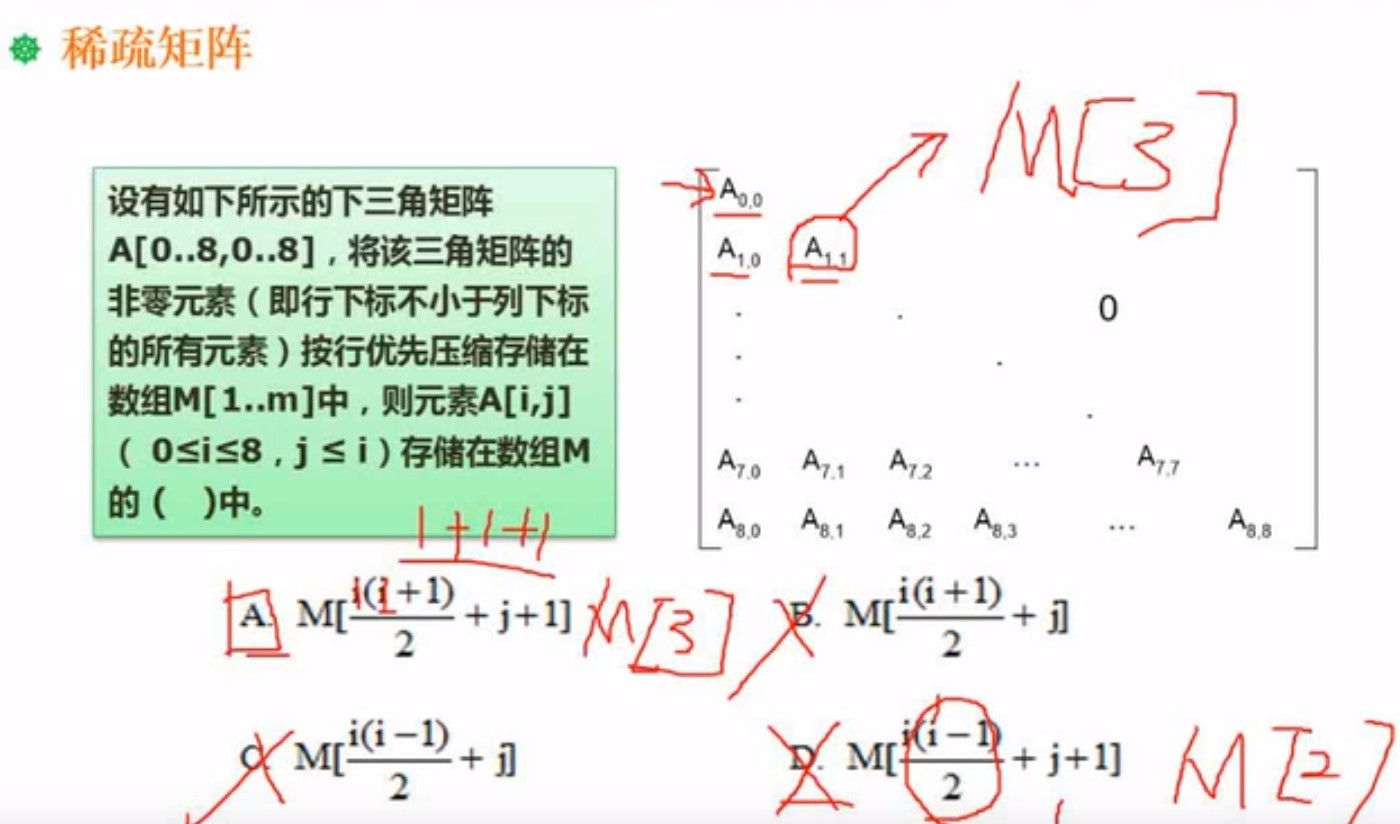
1.2 矩阵 （代入法求答案，重点）

考试经常考的是 稀疏矩阵的元素所对应的一维数组的下标

存储数据实际上都是按照一维数组这样，按照顺序存下来的

稀疏矩阵就是很多空位为0的情况

另一半不存的原因，可能是重复的，无向图存下来就是一个三角矩阵

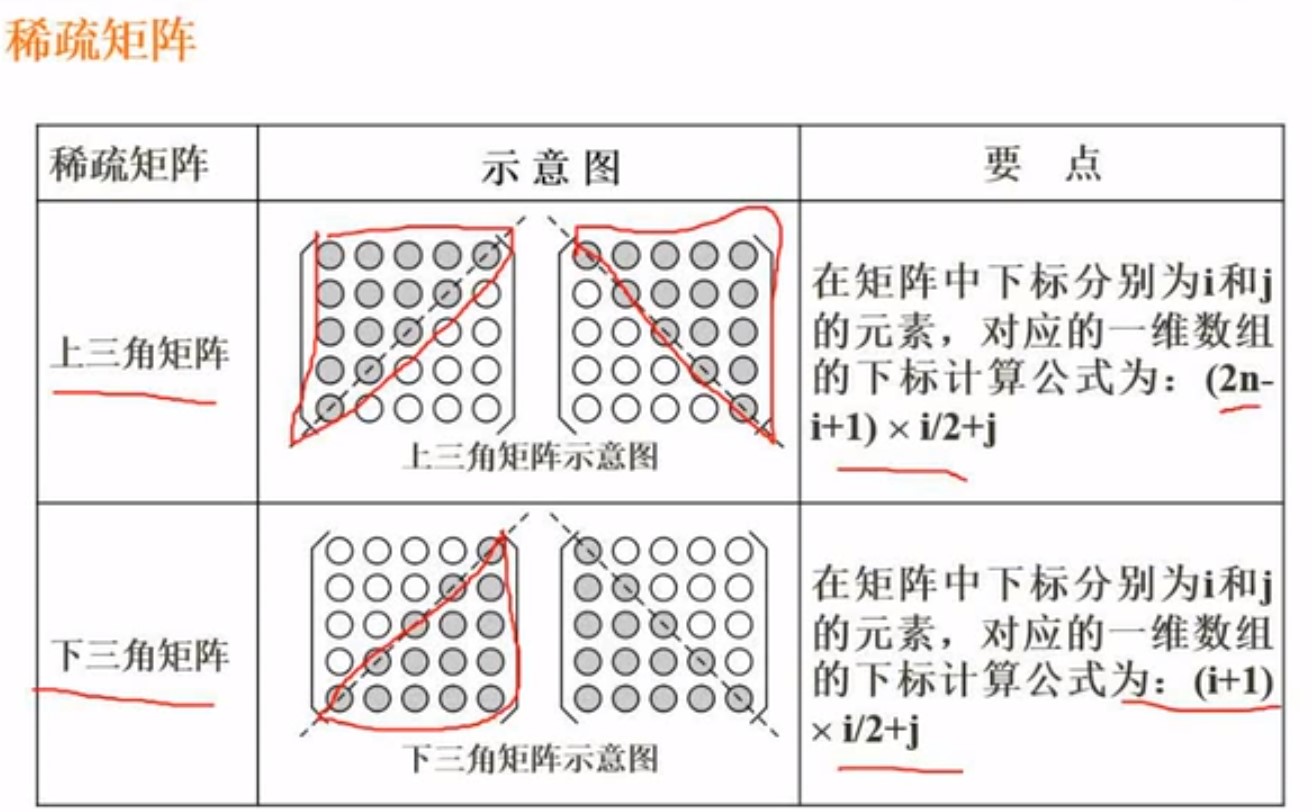
做这种题，考试就要用代入法，由题目得知存在一维数组是从索引1开始的

将下标带入公式，看能不能算出存在以为数组正确的地方，正确的索引位置

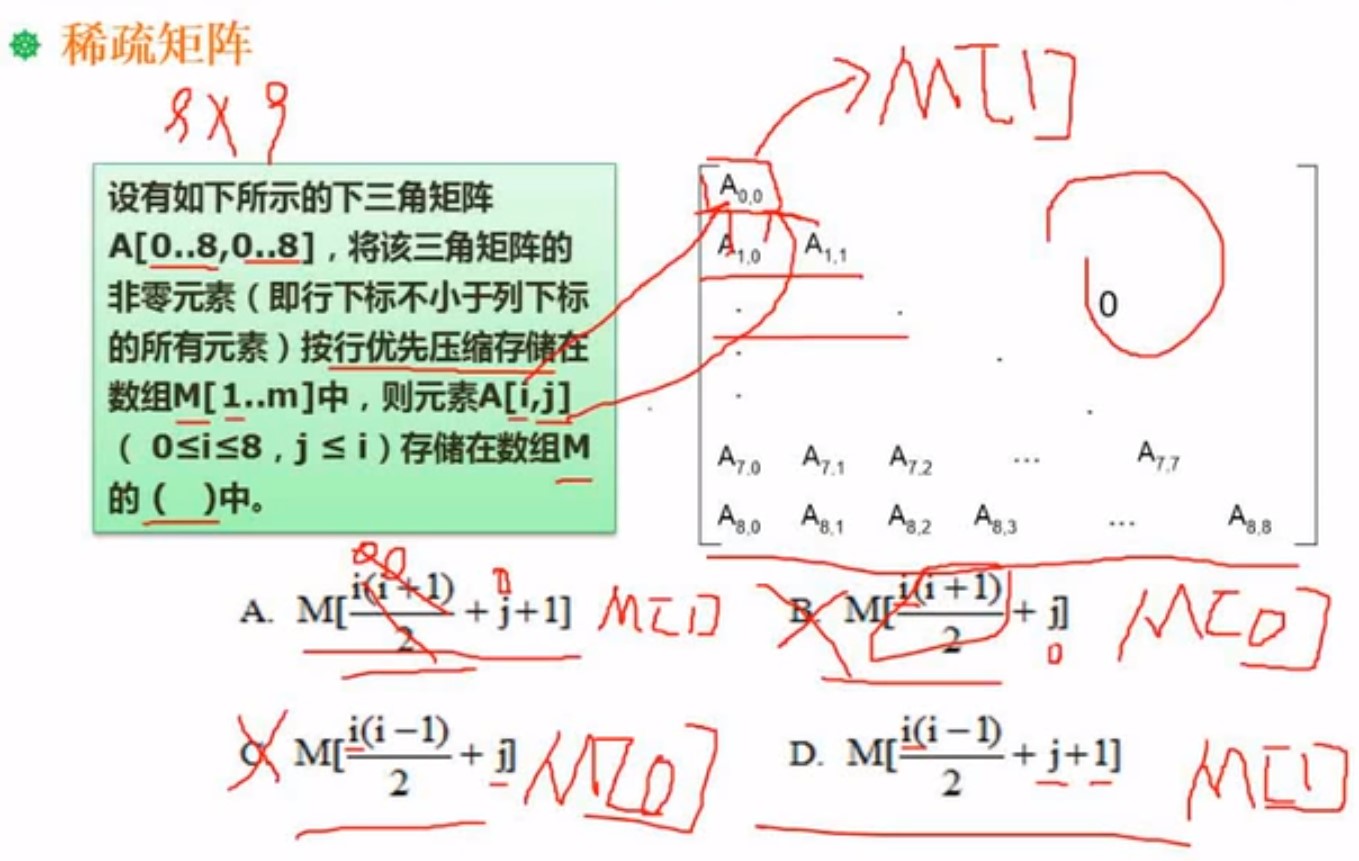
按照行存，就是从第一行接着第二行，慢慢按照顺序存进数组，

2.线性表

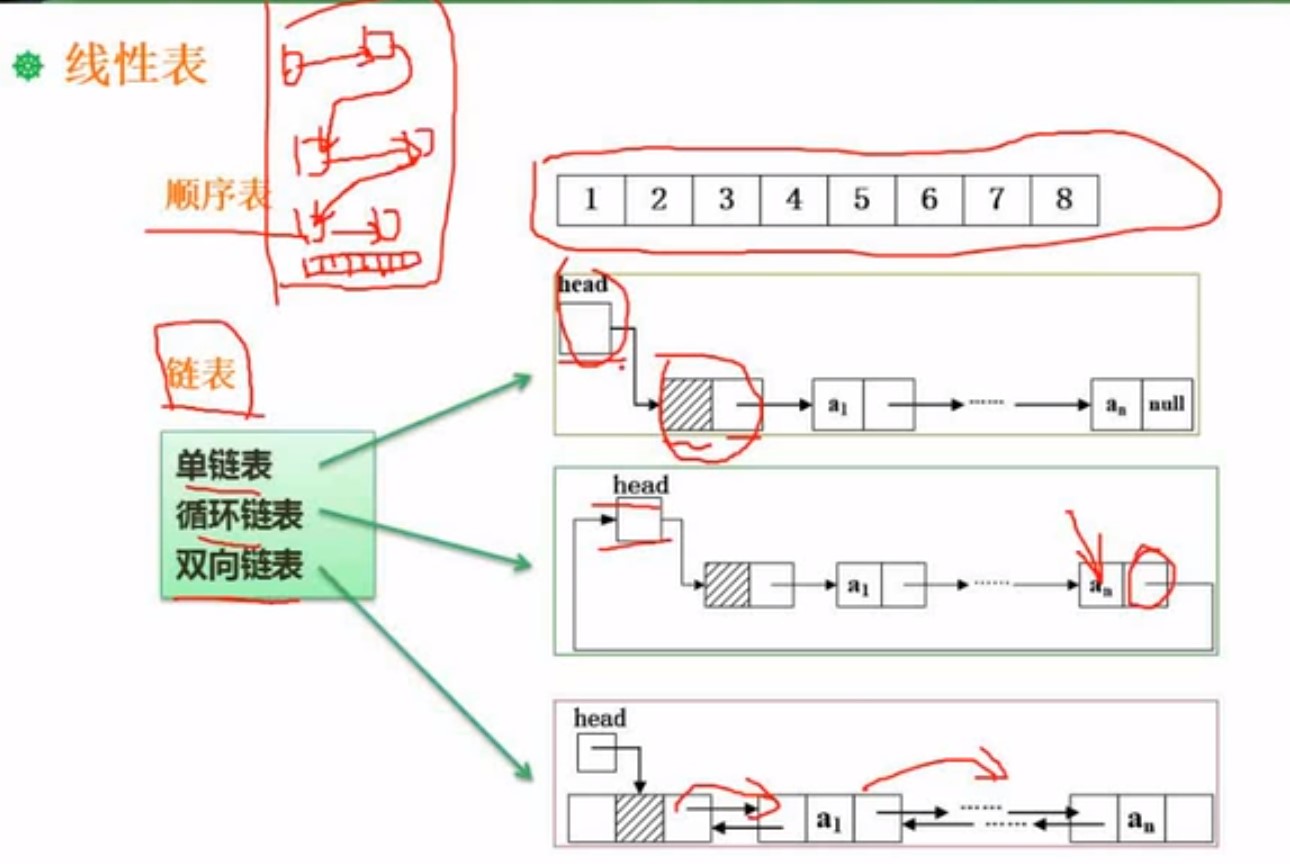
2.1顺序表和链表

线性表是线性结构的基本表现

单项链表的删除

• 就是当前节点的的next  = 被删除节点的next
  

就是将下一个地址值赋值给上一个

单项链表的添加

• 就是将插入的节点的next  = 之前前一个的next  就是将下一个的地址值进行赋值
  
• 接着再将原来的next = 插入的节点所在的地址
  

就是当前节点的的next  = 被删除节点的next

就是将下一个地址值赋值给上一个

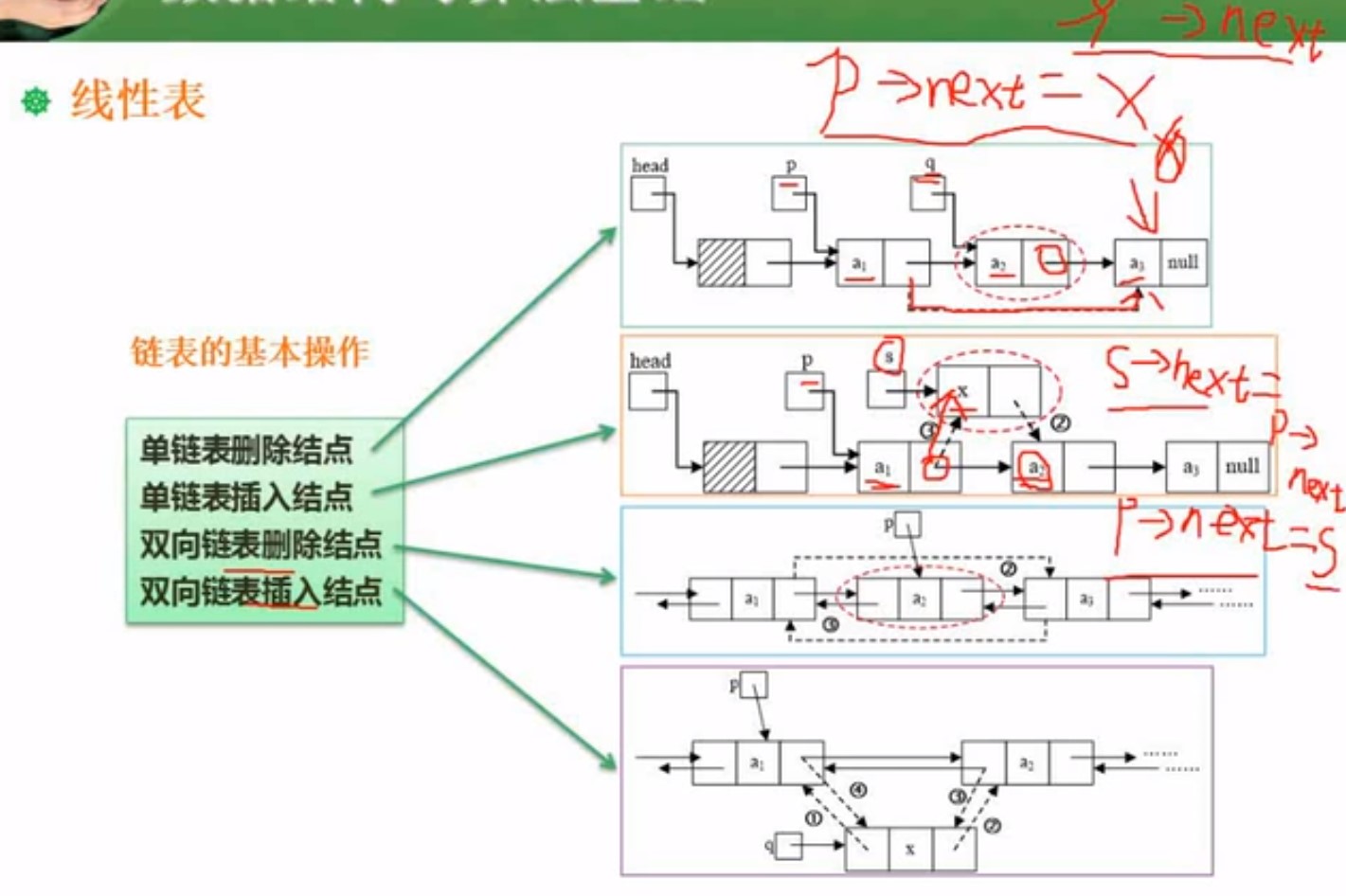
单向链表有有节点和没头节点，就是头节点不存信息

引入头节点名可以让所有的节点的操作方式一致的

如果头节点存了内容，那不同的头接待你可能采用不同的操作方式

2.2 顺序存储和链式存储

链表，的节点，并不是内容这么大，实际就这么大，还要存指针的

例如一个节点，2bit存内容，1bit存指针，就是利用率 66%

顺序存储如果有顺序的内容，二分查找比较快

链表度数据要从第一个开始，一个一个往后移动。顺序，直接获取例如a[5]

2.3时间复杂度

2.4队列和栈 （重点）

• 循环队列

进一个，tail(尾指针)往后走一位  (例如0号位存了东西，尾指针往后走一位到1号位)

出一个，head(头指针)往后走一个    头指针指向是存数据的，尾指针是执行下一个位置，不存数据的

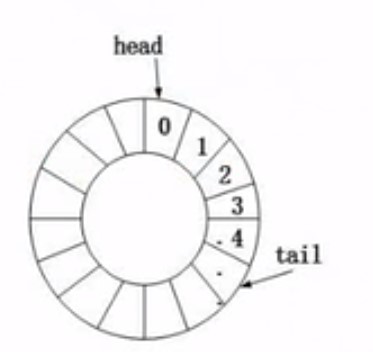
队空 tail(尾指针) == head(头指针)，

队满，头指针和尾指针又走到一起  

所以一般我们循环队列，不存满全部数据,,留一个空位，例如，可以存5个，但我们只存4个，当4加1再取余总数，余数是0  == 头指针位置。这样来判断队满。 (tail+1)%size = head 队满

一般如果知道队头，还有存了多少个数据，来求尾指针位置，一般跟队列能存总数取余

• (对头位置+当前存的数量)%能存的总数  =  尾指针位置

例如对头在4的位置，知道存了3个数据，(4+3)/5 = 2  ,2就是尾指针位置

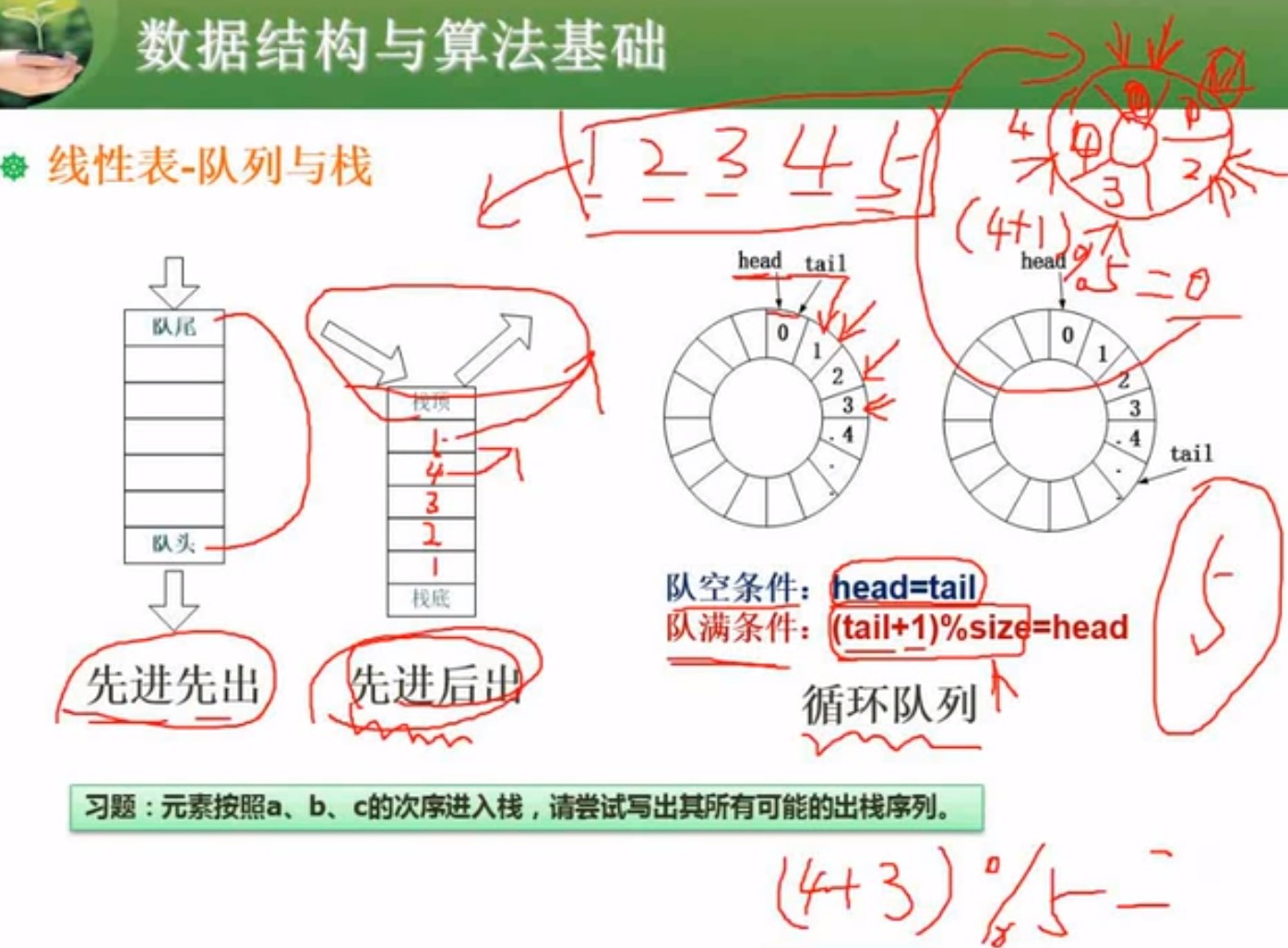
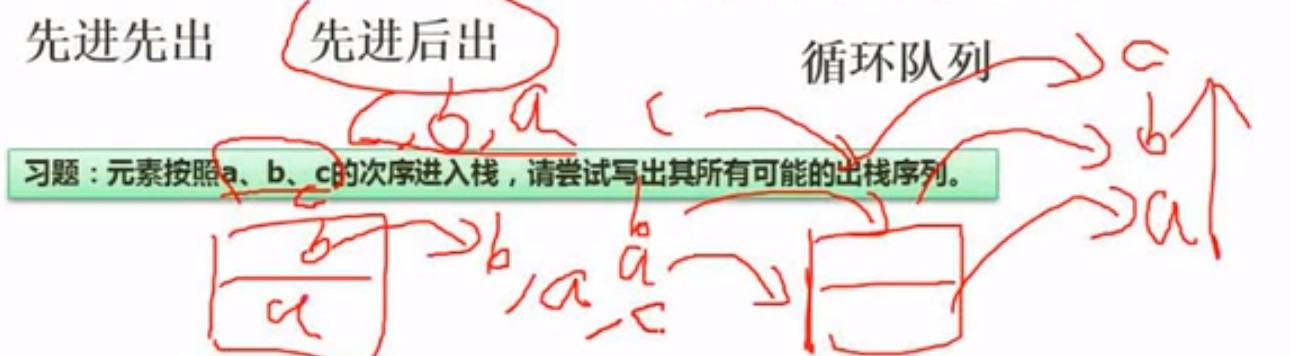
以某种顺序入栈，但是出栈顺序可以不一样的，例如你先入a,接着立马出a

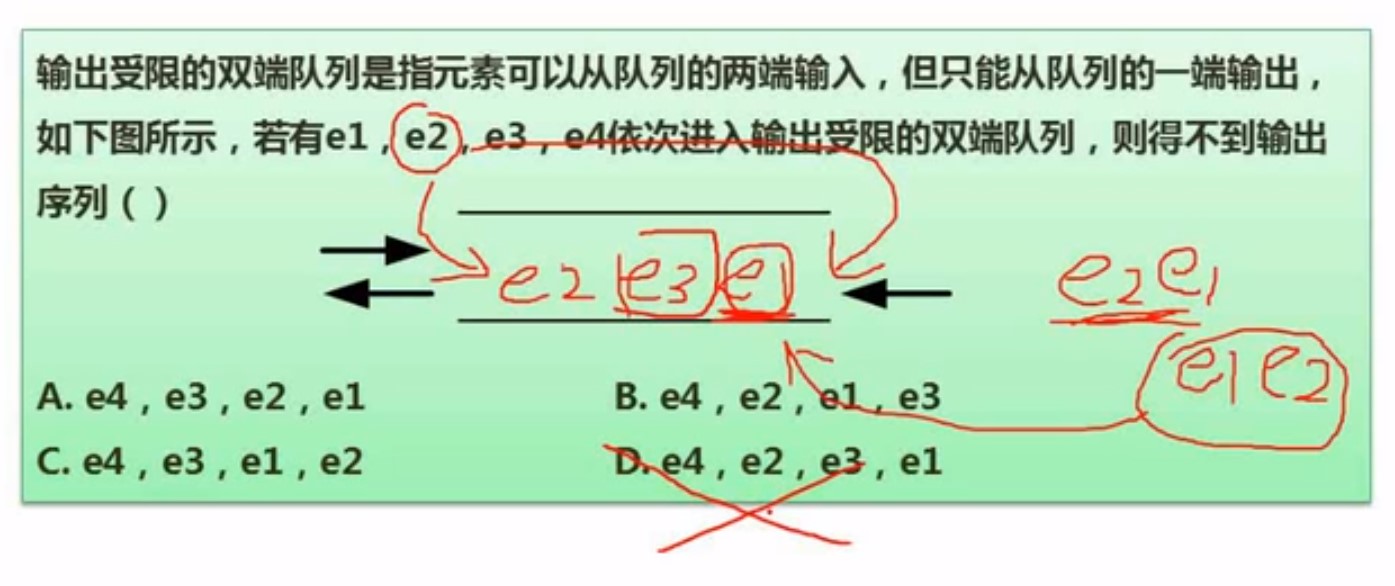
下面这种题，我们把答案带进入里面，来进行判断，左右都可以进，看能不能排成这样队列出来

能排出来，说明就行，排不出来说明就不行

3.广义表（重点）

• 长度就是最外层包含多少个元素的问题
• 深度就是括号的最大嵌套层数
• 表头就是最外层的第一个元素
• 表尾是除了最外层的第一个表元素的其他部分组成的新的广义表

4.数和二叉树

4.0常用二叉树概念

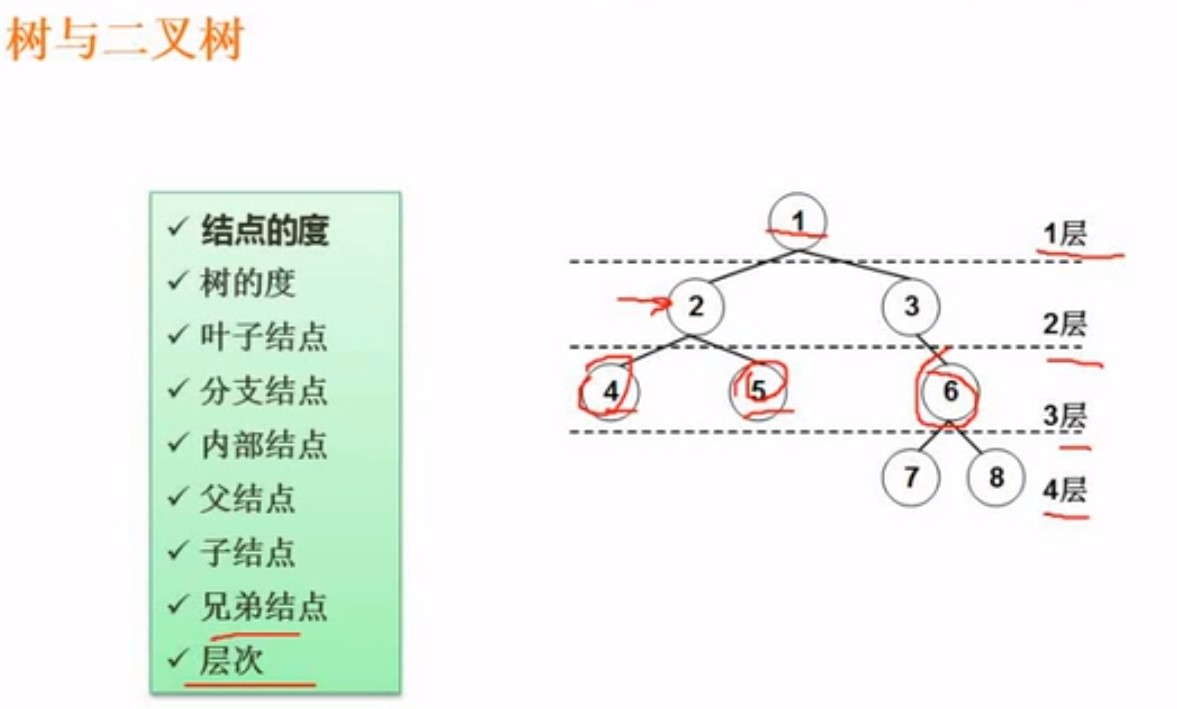
4.1基本概念

• 节点的度：这个节点有多少个子节点
• 树的度：就是这个树的所有节点，子节点最多的节点的度(例如树的全部节点，最大的节点的度是3，所以数的度是3)
• 叶子节点：就是没有子节点的节点
• 分支节点：有子节点的节点
• 内部节点：不是叶子节点，也不是根节点，中间那些
• 父节点和子节点：相对关系的
• 兄弟节点：就是属于同一个父节点的全部节点
• 层次(深度)：看节点一共有多少层

4.1 二叉树

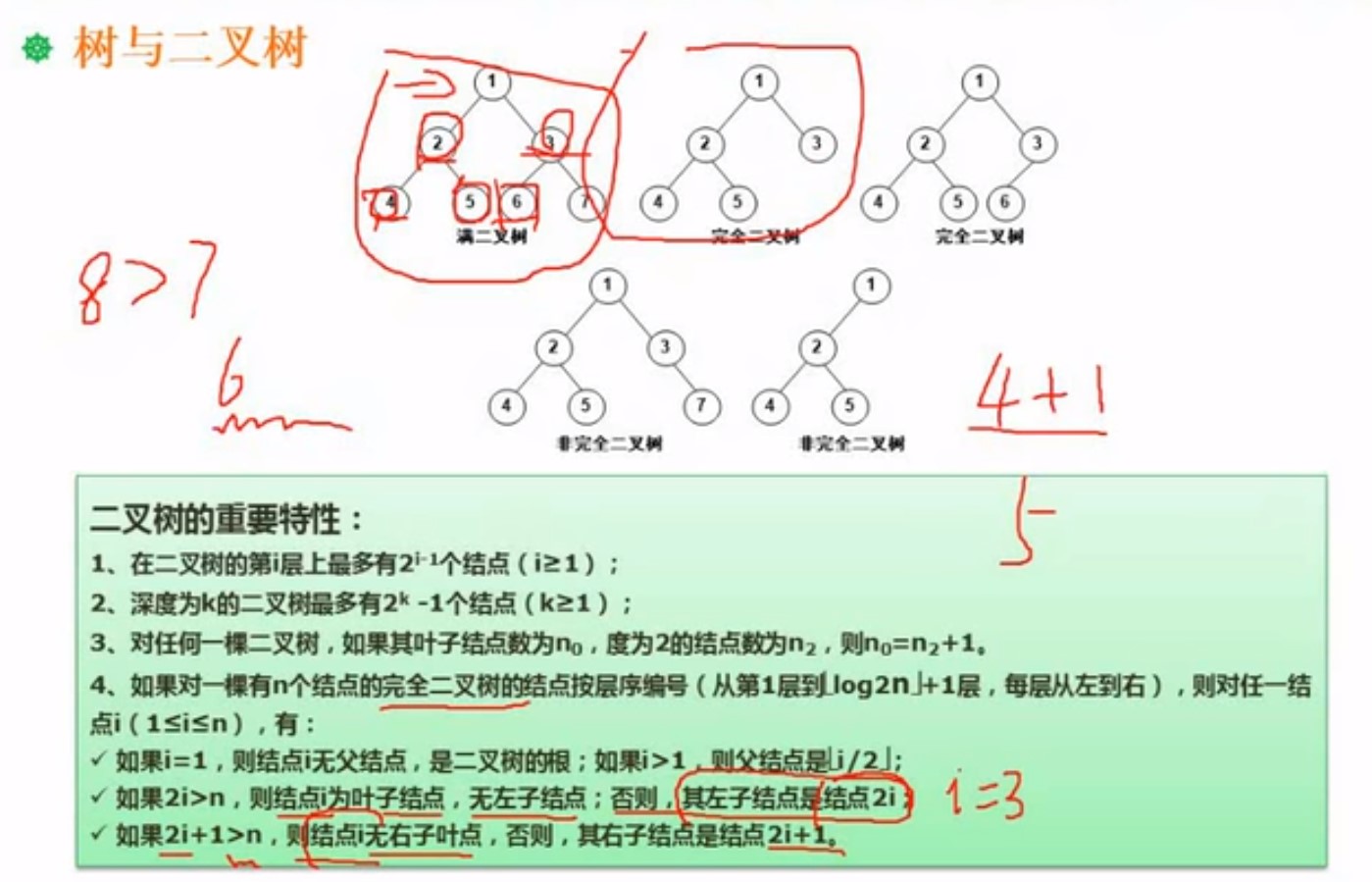
• 满二叉树：就是每层节点都是满的，没有缺失节点的
• 完全二叉树：除了最后一层，上面一层节点没有缺失的，且缺失的节点的最后一层，是从左到右满的或者缺的，不能隔着一个，就缺
• 非完全二叉树：就是一层一层来，左边没有排满的，隔着来
• n0就是度为0的节点总数，n2就是度为2的节点总数。 n0 = n2 + 1 (这个记住就行)

完全二叉树，因为是按照顺序一层一层的排下来，且是从左到右，左边都排满，这样的好处

是简单的公式就能求解问题(下面图的第4点)

4.3二叉树的遍历 （重点）

做前中后遍历，就是不停的划分 根左右节点，从大到小，小里面再来分根左右，一层一层写即可

层次遍历:从上到下，从左到右

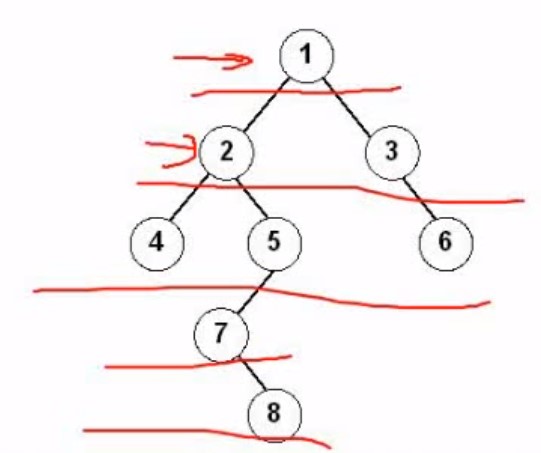
前中后遍历是根节点什么时候访问来命名的,区别就是根节点什么时候访问

• 前序遍历： 根结点 ---> 左子树 ---> 右子树
• 中序遍历： 左子树---> 根结点 ---> 右子树
• 后续遍历:    左子树---> 右子树 ---> 根结点 

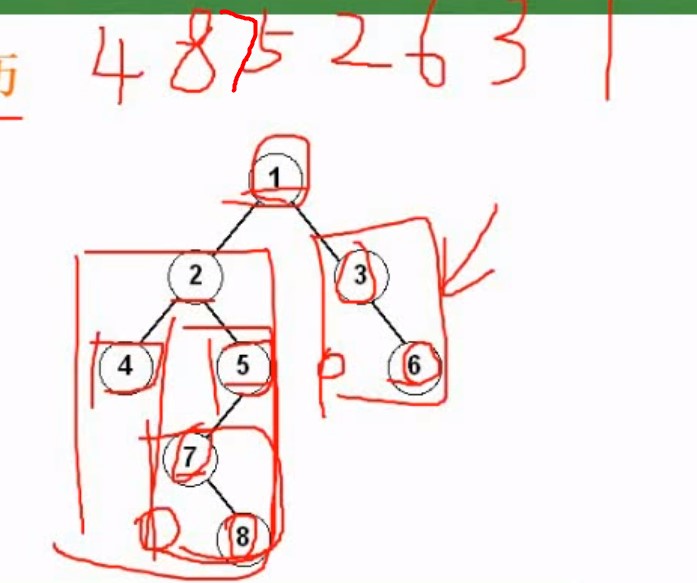
前序遍历 12457836

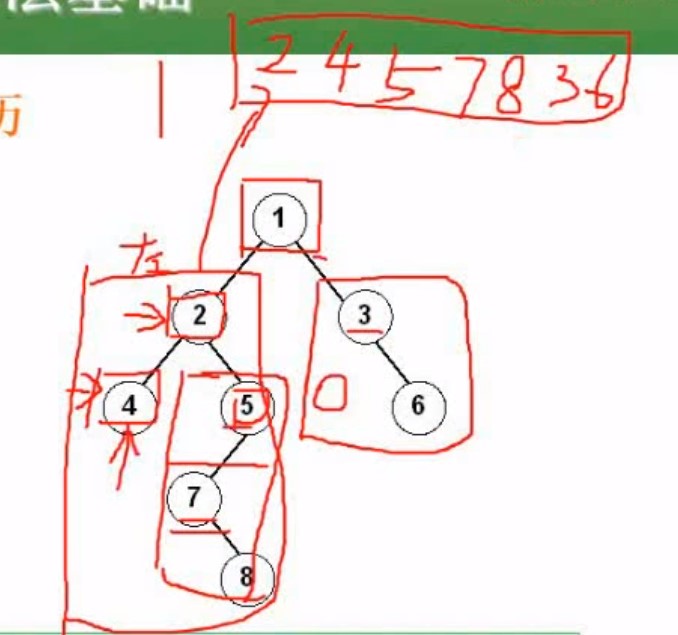
中序遍历 42785136 

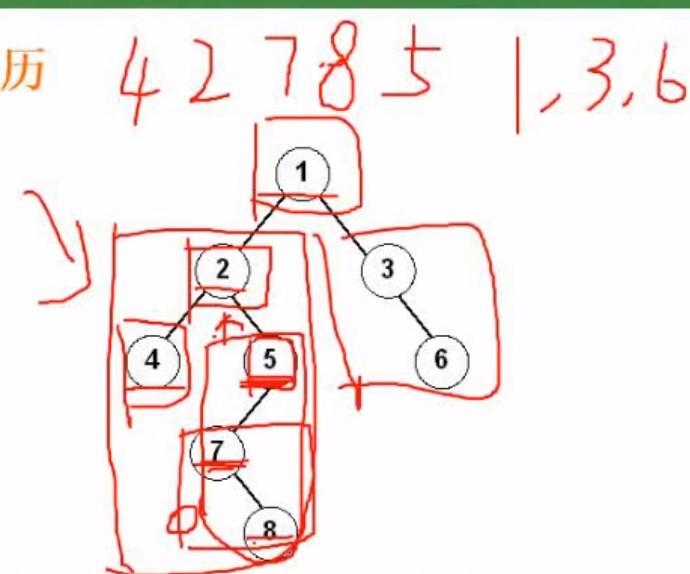
后序遍历  48752631

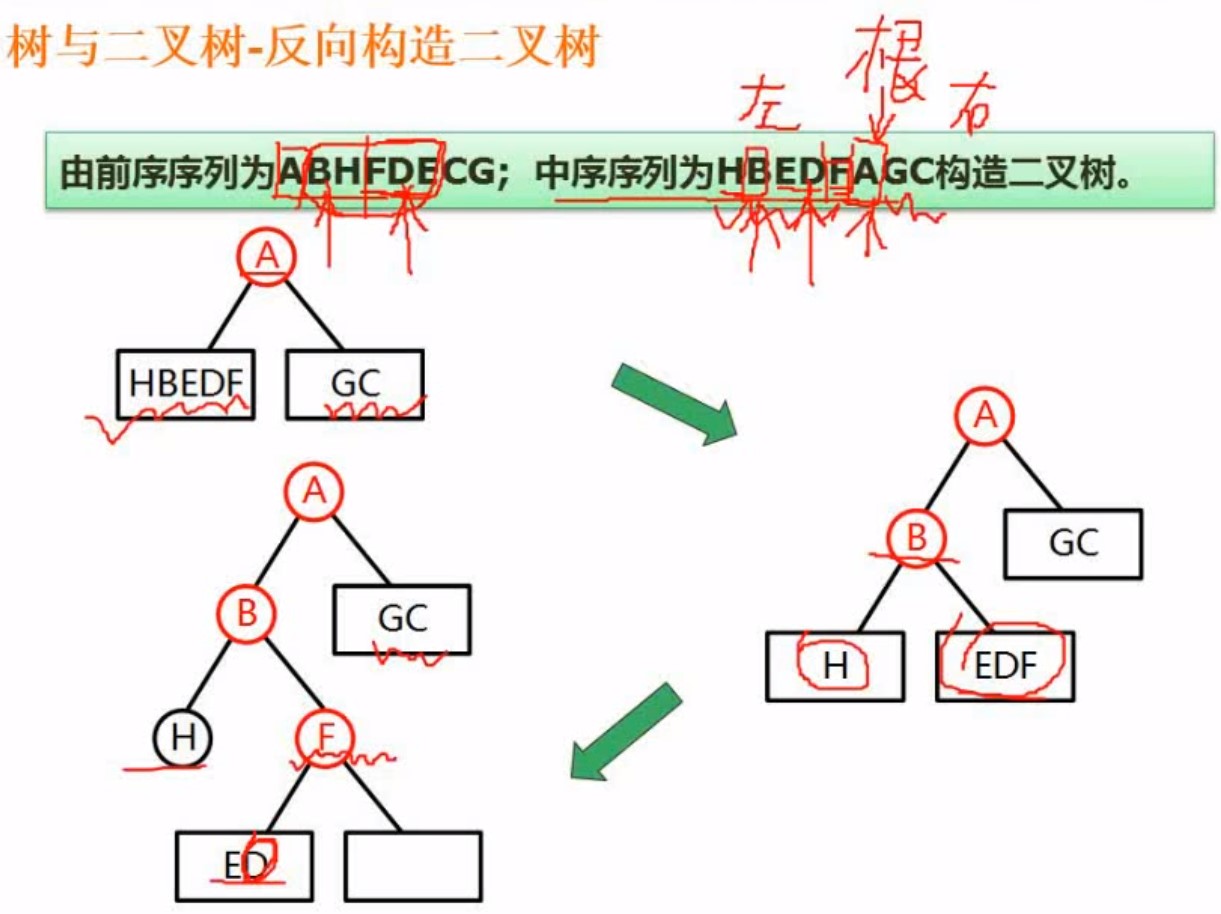
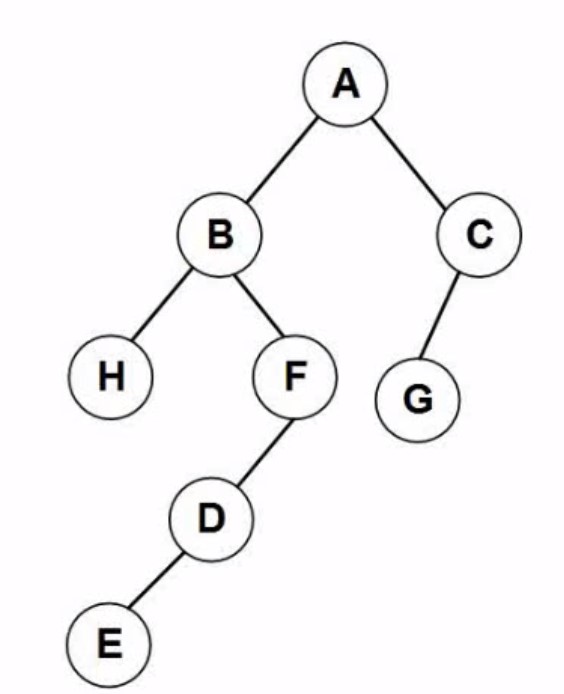
4.4反向构造二叉树

如果有前和中，或者中和后，可以构造出树

但是只有前和后是构造不了树出来的

比如知道前和知道中，如下

首先记得左，肯定是根节点，然后将这个根节点拿去中来区分，那些是左部分哪些是右部分

• 前序，左边访问的第一个是根      前和后序是用来确定哪个是根
• 后序，右边访问的第一个是根
• 中序，是根据上面得知的根，将节点分为左右两份，区分哪边是这个根节点的左，哪边是这个根节点的右

以此来类推，从前后序拿根，接着到中序来区分左右部分，一层一层来，分割左右的部分，再在分割的左右来进行进一步划分

简记：先前后序拿根，去中分左右

4.5树转二叉树

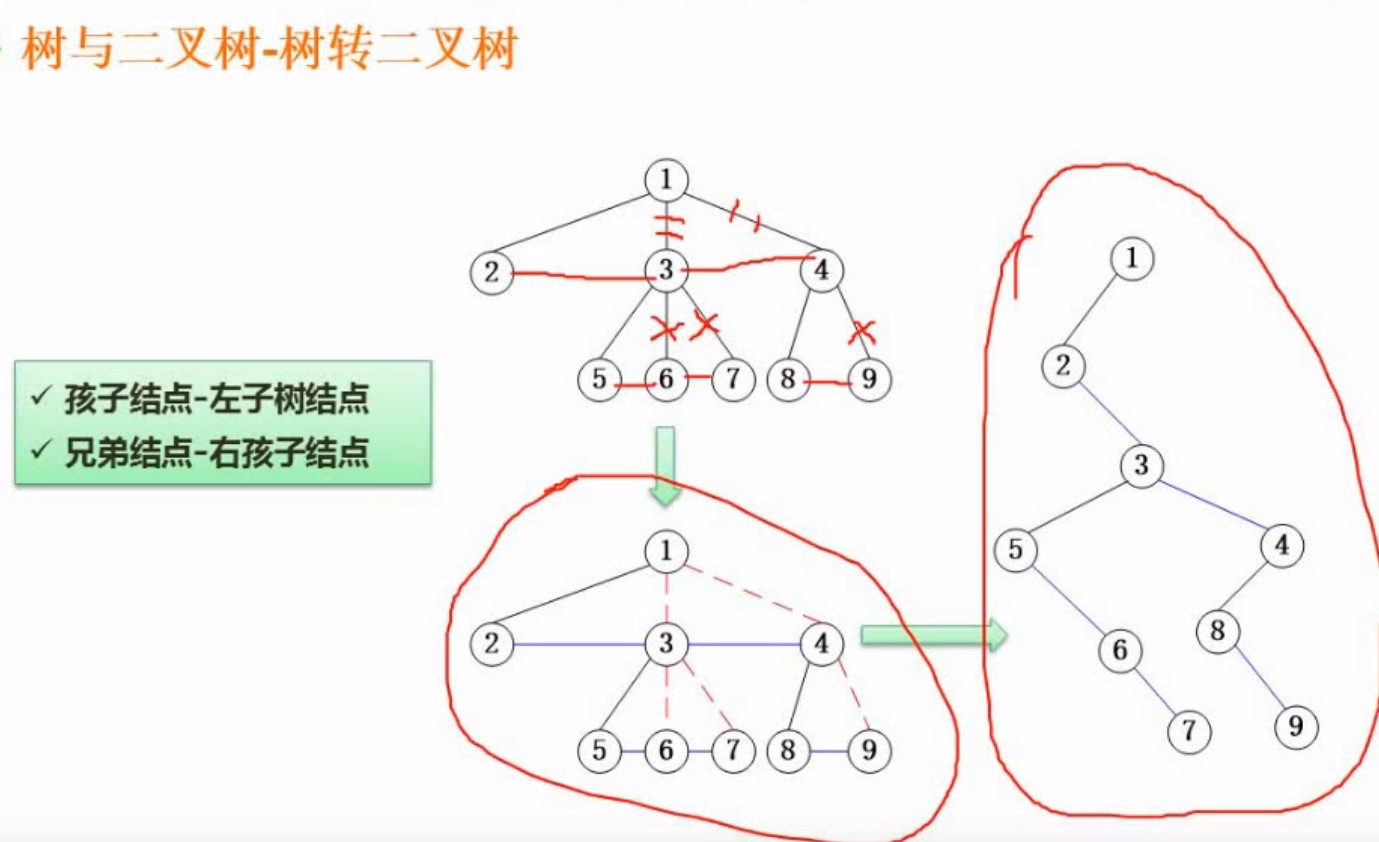
将普通的树转为二叉树

• 原始做法

第一个左孩子节点，作为左子树节点，接着右边的兄弟节点，就作为前一个的右孩子节点

例如 2是第一个孩子，2是左节点，3是2的兄弟，所以3是2的右孩子节点，4是3的兄弟节点，所以4是3的右孩子节点，以此类推

• 连线法

将所有的兄弟节点连起来，然后只保留第一个孩子跟父节点的连线，其他去掉，然后调整下即可

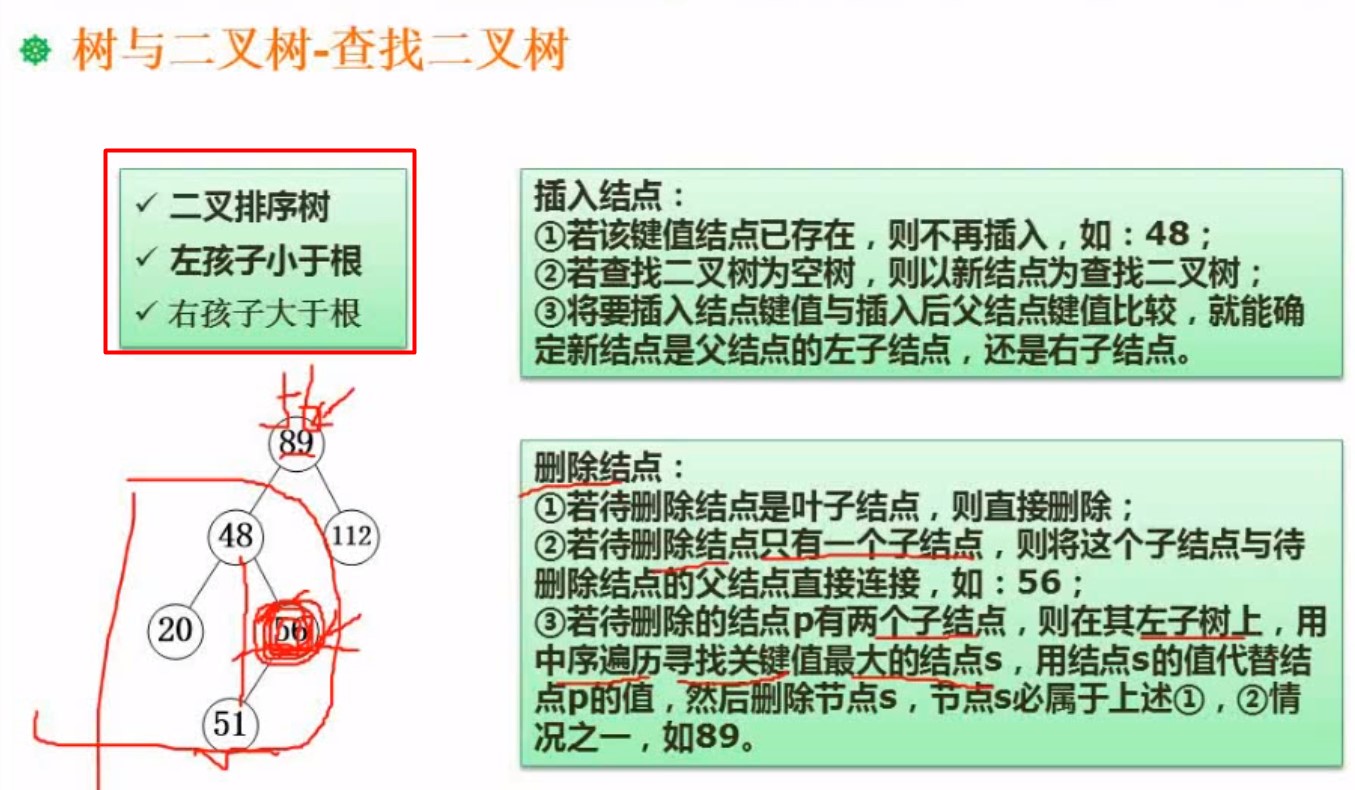
4.6查找二叉树(排序二叉树)

满足条件，左边比中小，右边比中大，左部分，右部分同样满足这个要求 ，这个就是排序二叉树 

我们做删除和插入操作时，验证记得大小关系的  左< 中 < 右

4.7 哈弗曼树(最优二叉树)  (重点)

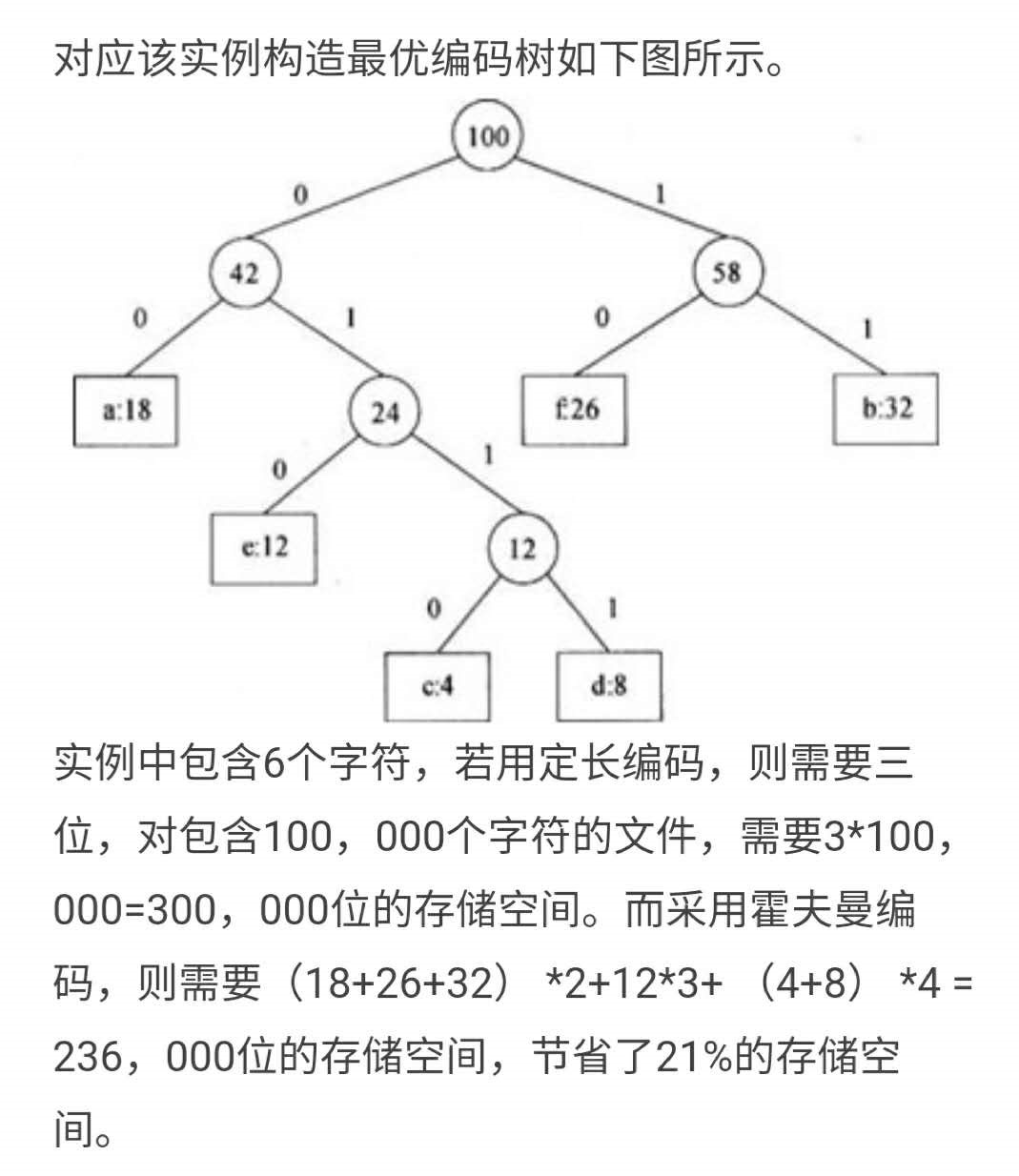
这个主要用于编码，用于压缩的，将原来的编码长度变得更短点，从而节省存储空间和传输带宽

属于无损压缩方式，就是压缩了可以还原，不会有信息的损失

• 树的路径长度：就是树的全部段的加起来的总和
• 权：每个叶子有个数字，代表某一种字符出现的频度
• 带权路径长度：就是从根节点到节点有多少段，接着    段数*权 == 带权路径长度   如下图  2的带权路径长度  2*2 = 4
• 树的带权路径长度(树的代价)：   把所有叶子节点的带权路径长度加起来，就是树的带权路径长度

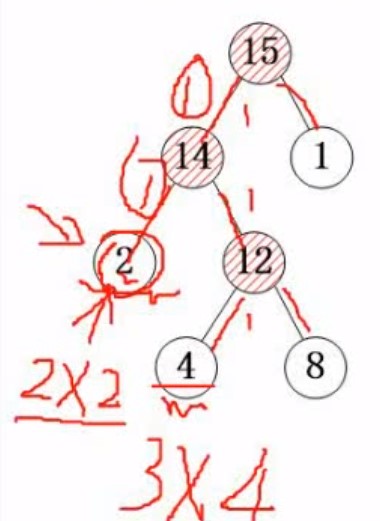
构造哈夫曼树，就是树的带权路径长度最小

做法就是不停的将最小的两个值，加起来，放进权里面，然后再取最小的两个相加

相加得到的也放进权值堆，再从堆中拿

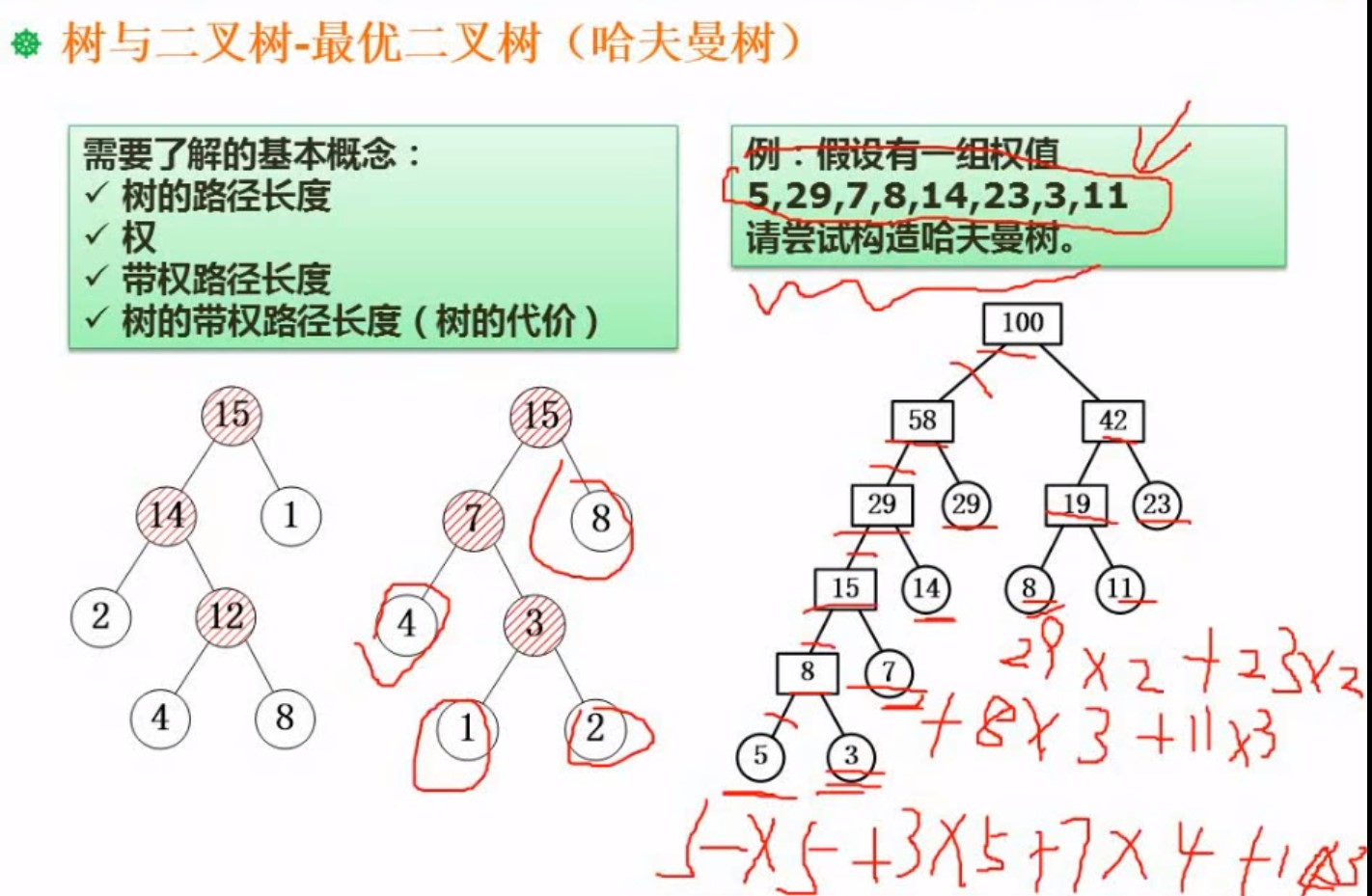
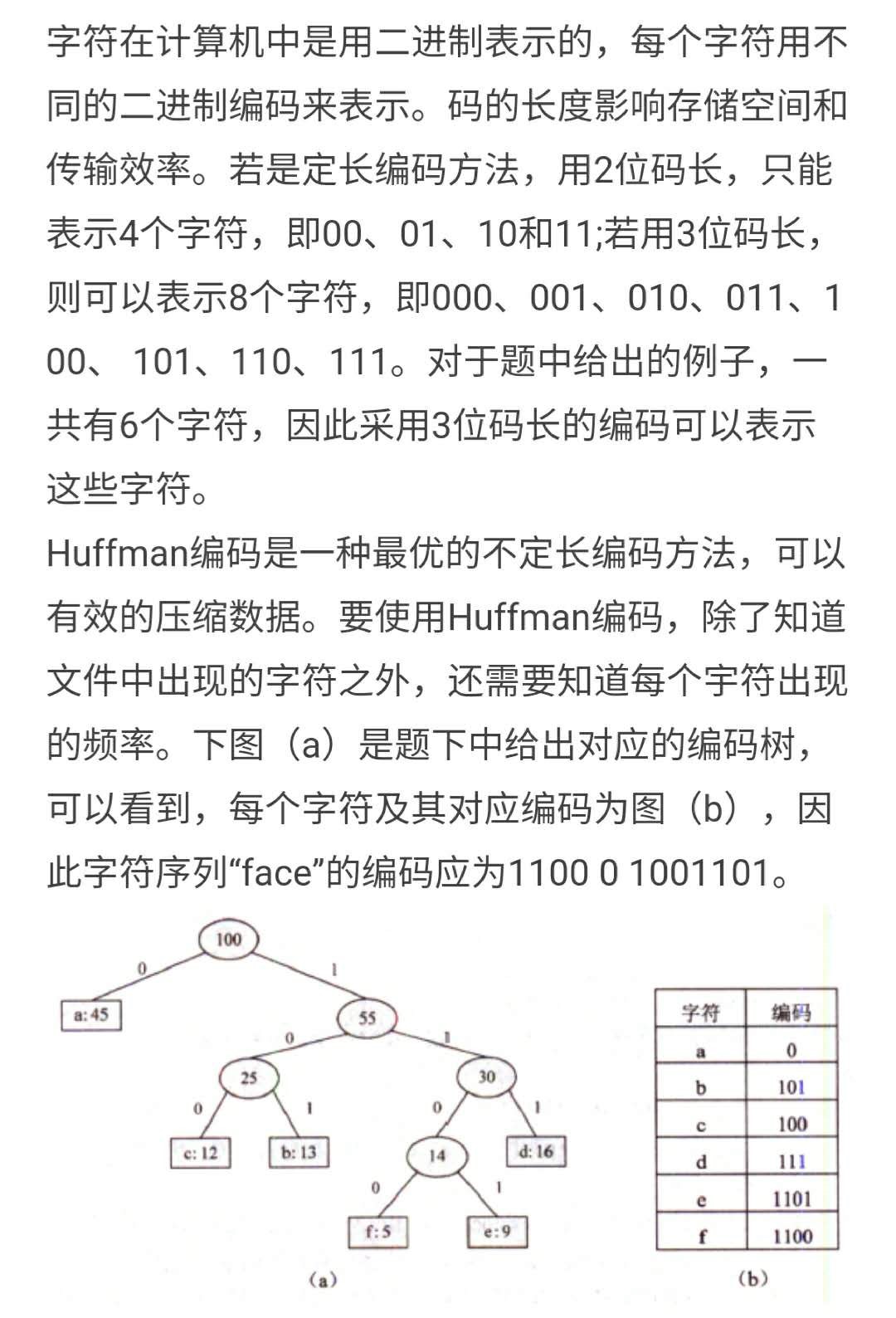
哈弗曼编码问题 （重点）

哈弗曼编码是贪心法

左0，右1

常用的 一般是  定长编码是 3  (一个字符多长)  ，每个编码都是这么长

可变编码是经过哈弗曼编码是经过哈夫曼树，改为可变字长    ，出现频率是权值

先根据总字符*定长编码  求出总的空间

然后画出了哈夫曼树，就求树的带权路径长度，这个就是压缩后的总空间        

接着求节省了多少  压缩率，看着做就行

6个字符，即 2的k次方大于题目的字符即可

得出定长编码

画树时，从下到上，每一层都是从左到右变大，这样0和1标注才正常

4.8线索二叉树

在二叉树的基础上有些虚线连接在一起

出现线索二叉树的原因是，普通的二叉树，节点左右节点的指针是空的，没有指向

所以想利用起来，主要用于遍历

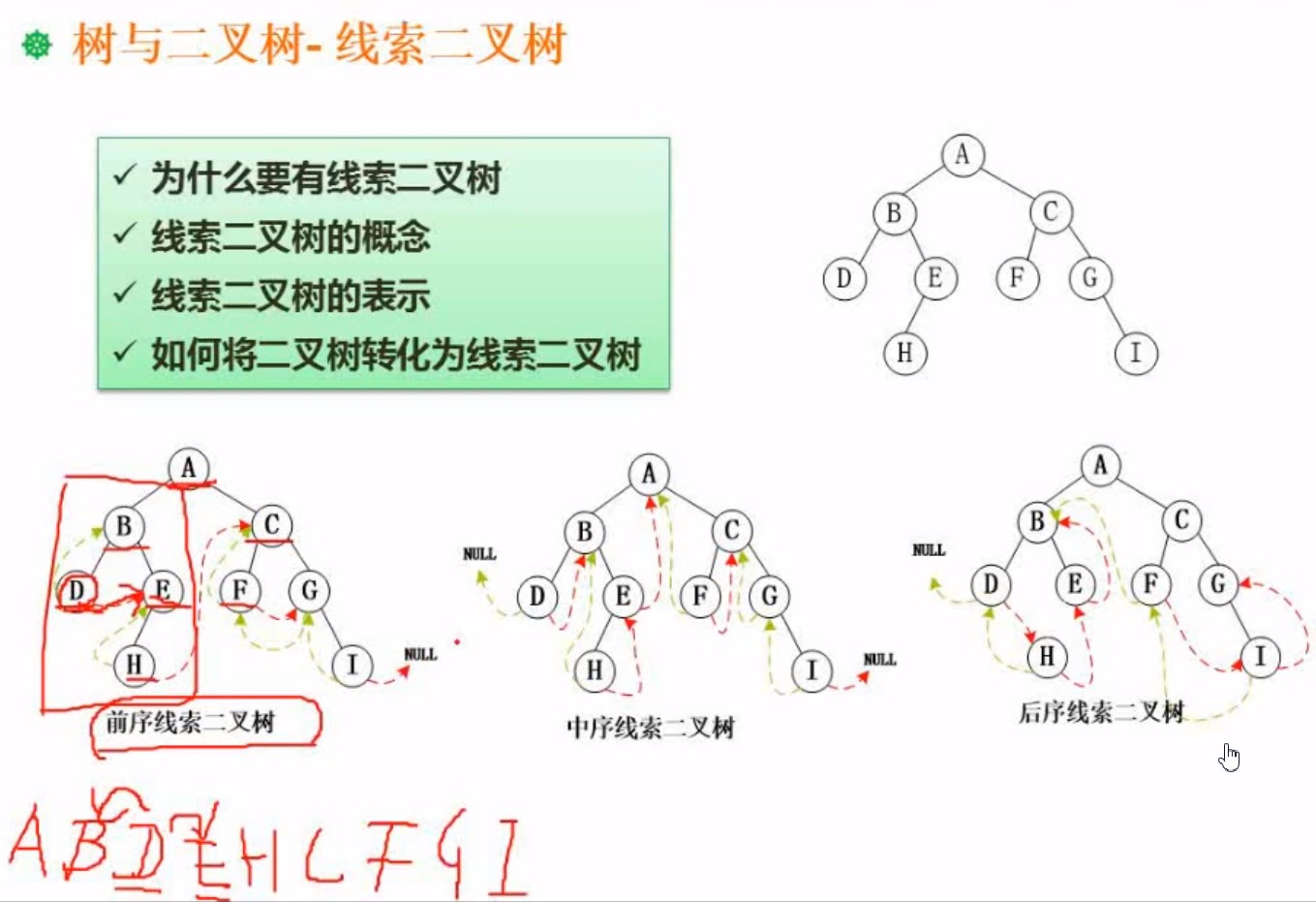
考试考的话，先根据题目说的是前，中，后，然后写出遍历

然后根据写出来的遍历顺序，来画线，例如ABDEHCFGI    D左边是B ,就画指向B  右边是E就指向E

4.9平衡二叉树

就是排序二叉树越平衡，越好用，这样查找效率高

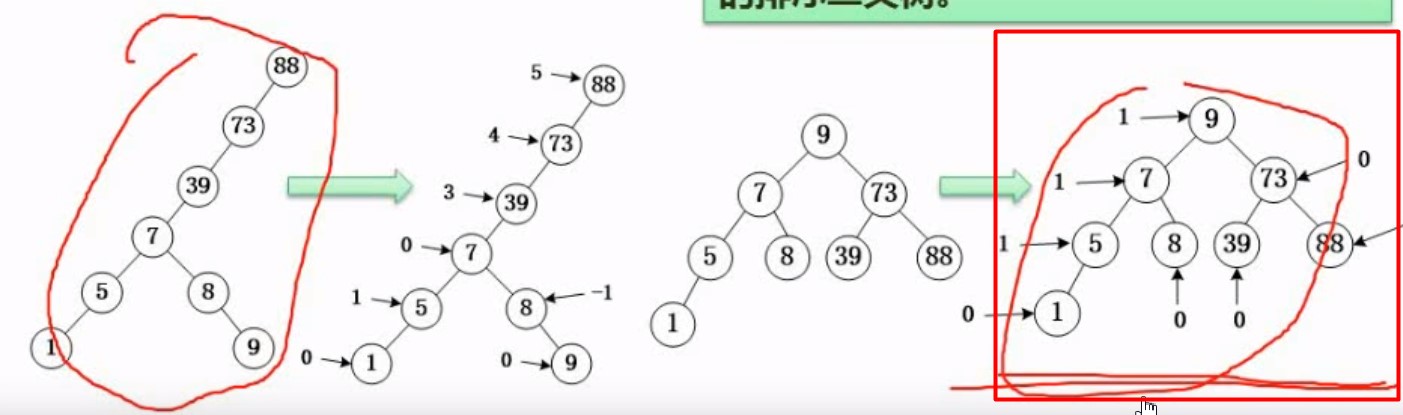
平衡度的计算 就是算左的节点的深度，减去右节点的深度的结果    叶子节点平衡度都是0

 

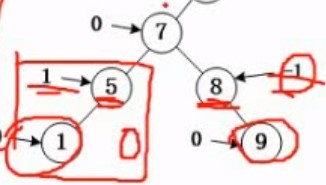
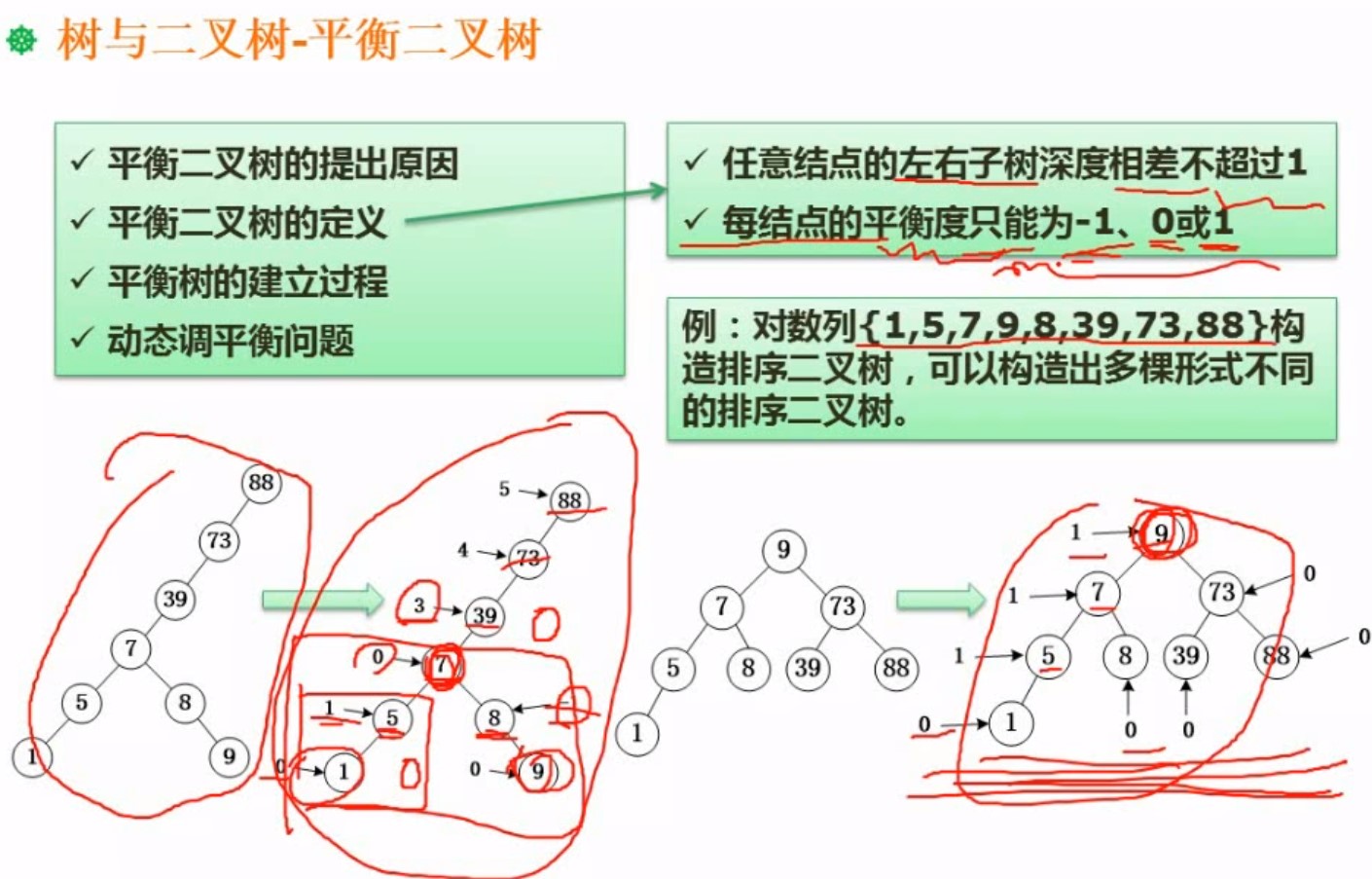
平衡调整，就是将原来节点的右边，慢慢进行调整，这个自己看着调节就行，看哪个适合作为中心节点

记得遵循查找二叉树的基本点

4.10题目

5.图(考察频率比树低)

5.1基本概念和存储

5.1.1 基本概念

• 无向图：每个节点的边都是没有方向性的
• 有向图：即边都是有方向的

无向图和有向图都有完全图。两种图的完全图如下

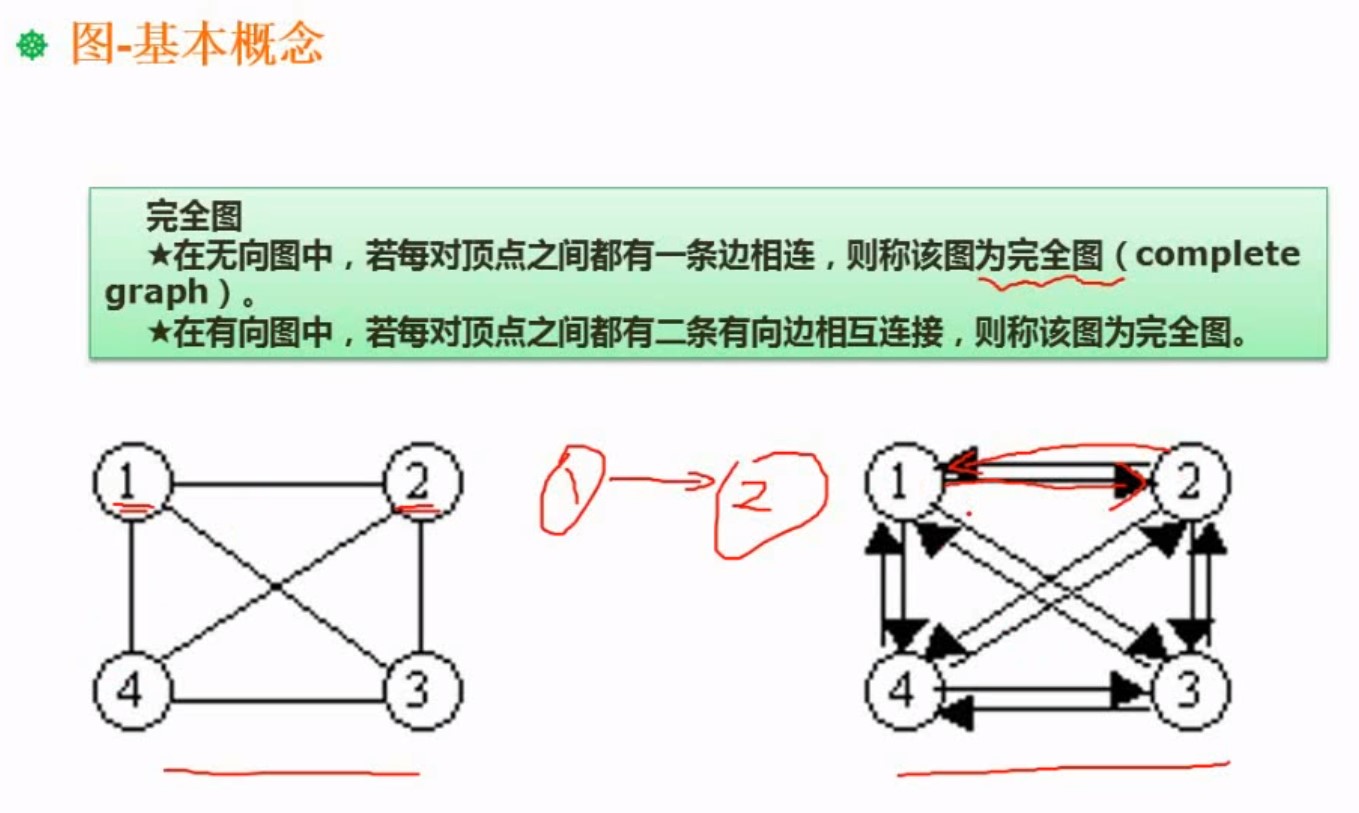
5.1.2存储(邻接矩阵)

有多少个节点就有  多少×多少的矩阵  例如 5个节点，矩阵5×5

由图画矩阵，按照这个点到那个点有没有线，有就1，没有就0

有向该矩阵非零元素数目为e

无向该矩阵非零元素数目为2e

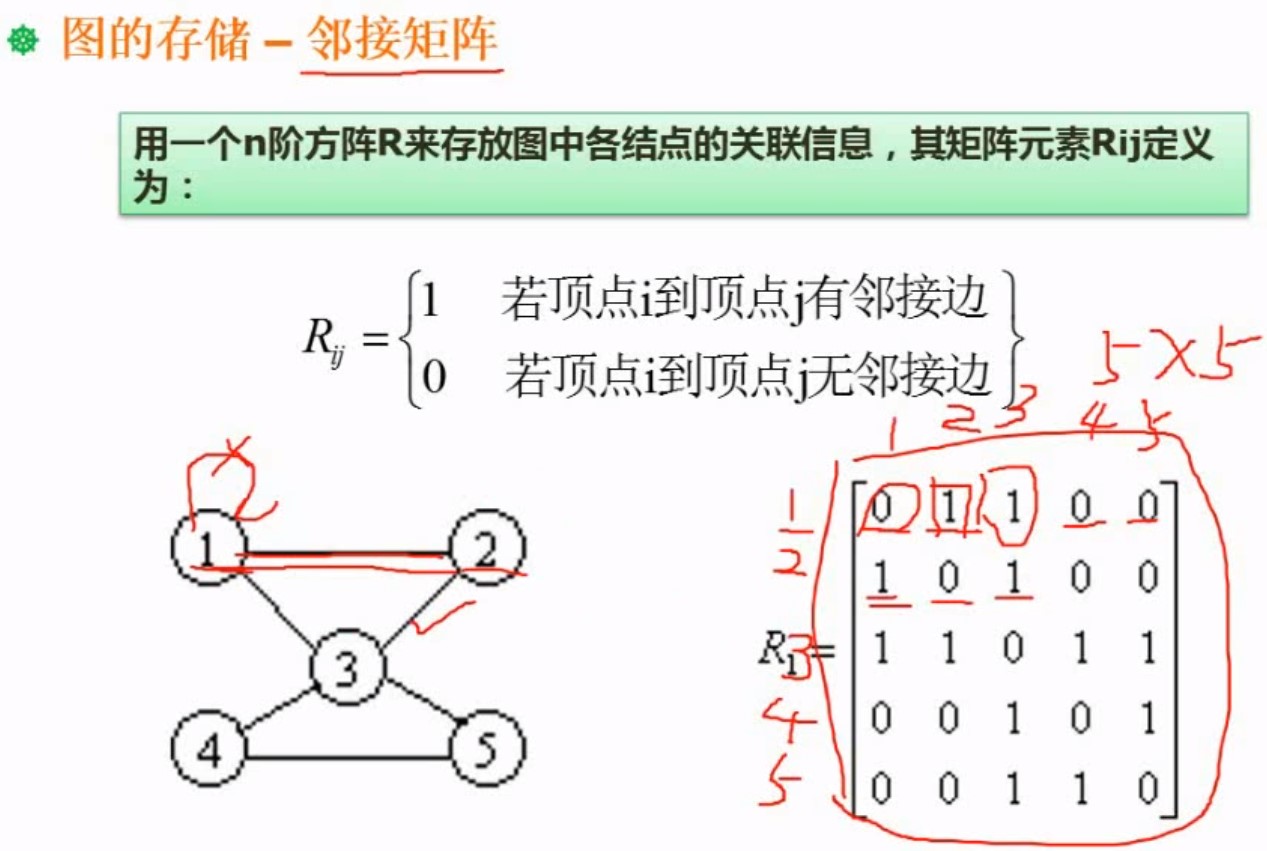
无向图的邻接矩阵有个特点，对接线可以对折，所以可以只存上三角或者下三角，可以节省存储空间

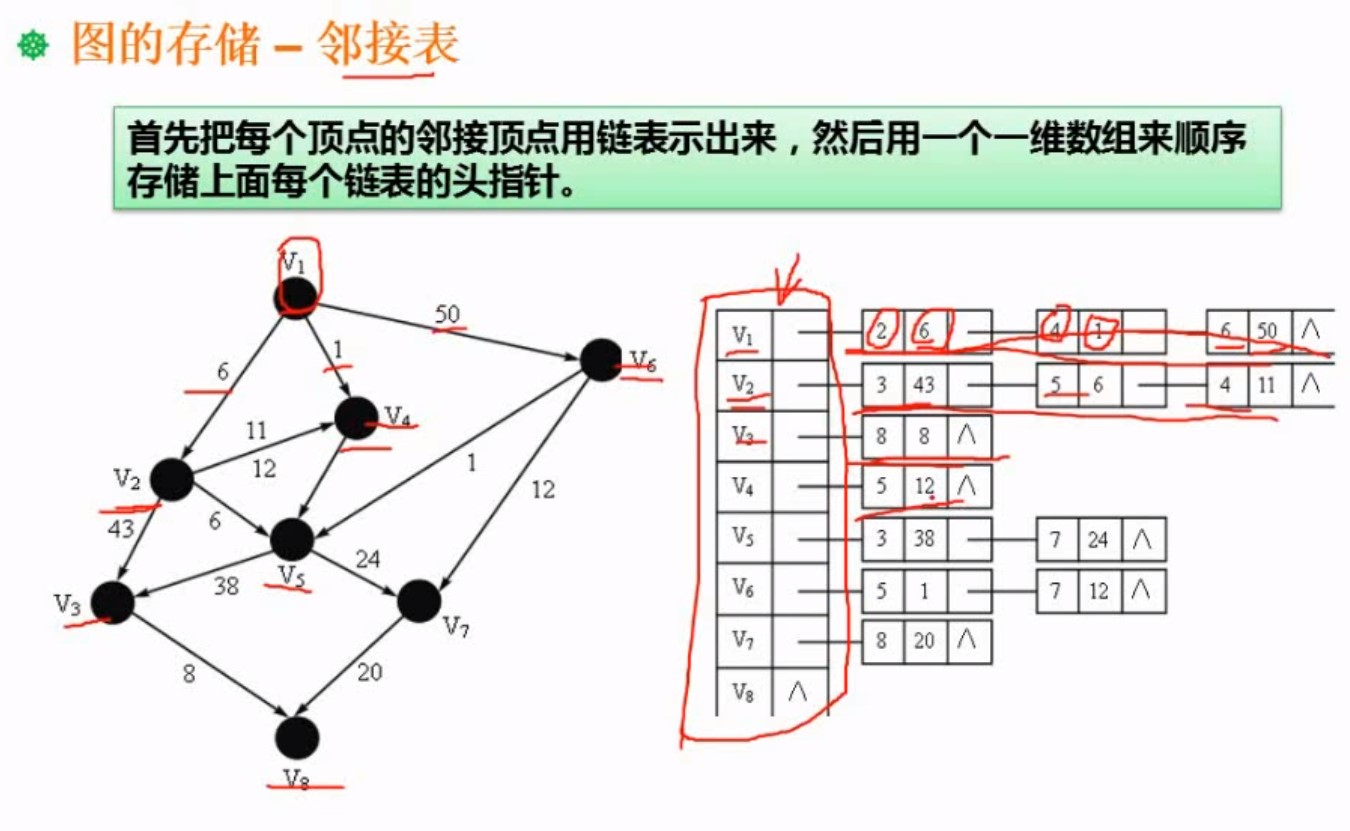
5.1.3存储(邻接表)

每个节点可以用表示可以到达哪个节点，距离多少，例如下面  v1 可以到  v2,v4,v6  ,所以分别连接起来，后面填的是到这个节点的距离是多少

就是数组加链表的组合，类似哈希表

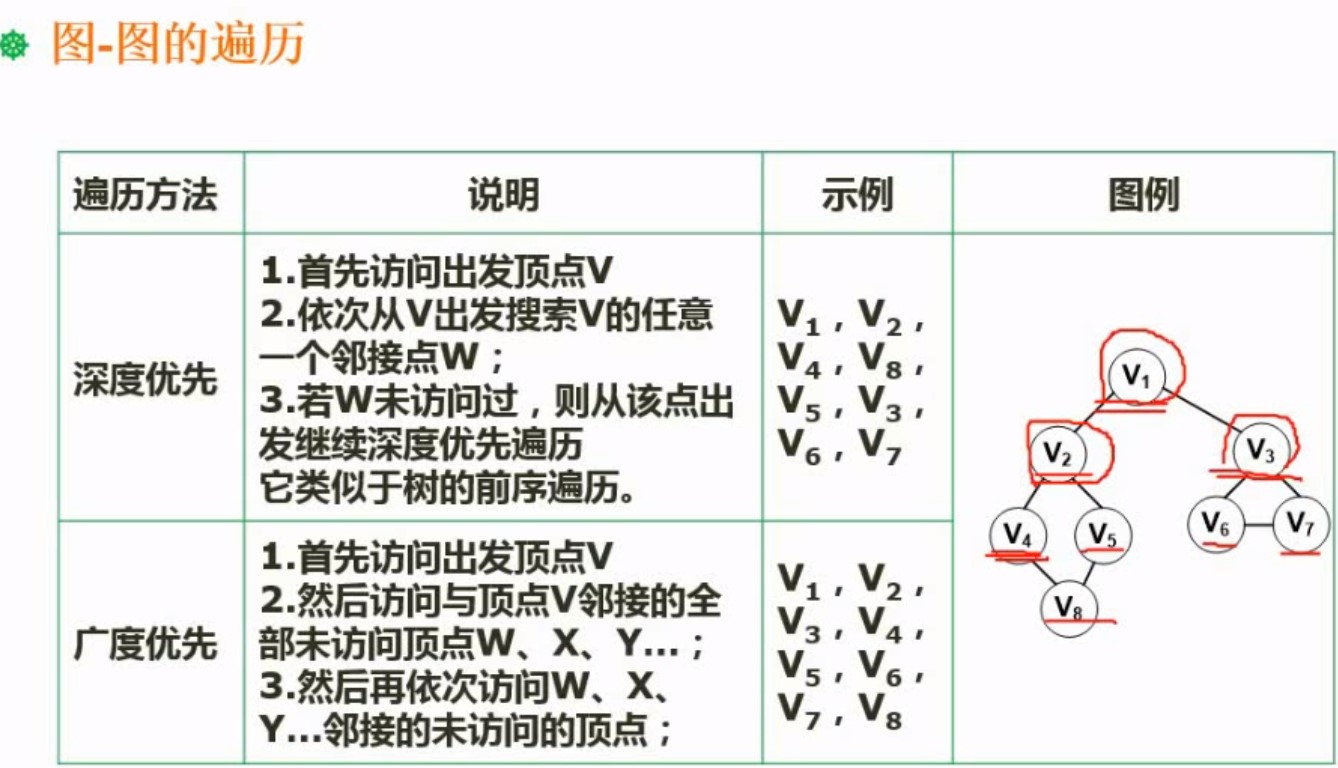
5.2图的遍历

深度优先：就是先一层直接到底，直到没有了，才退回去访问其他的

广度优先：就是先将一层的全部走完，再走下一层

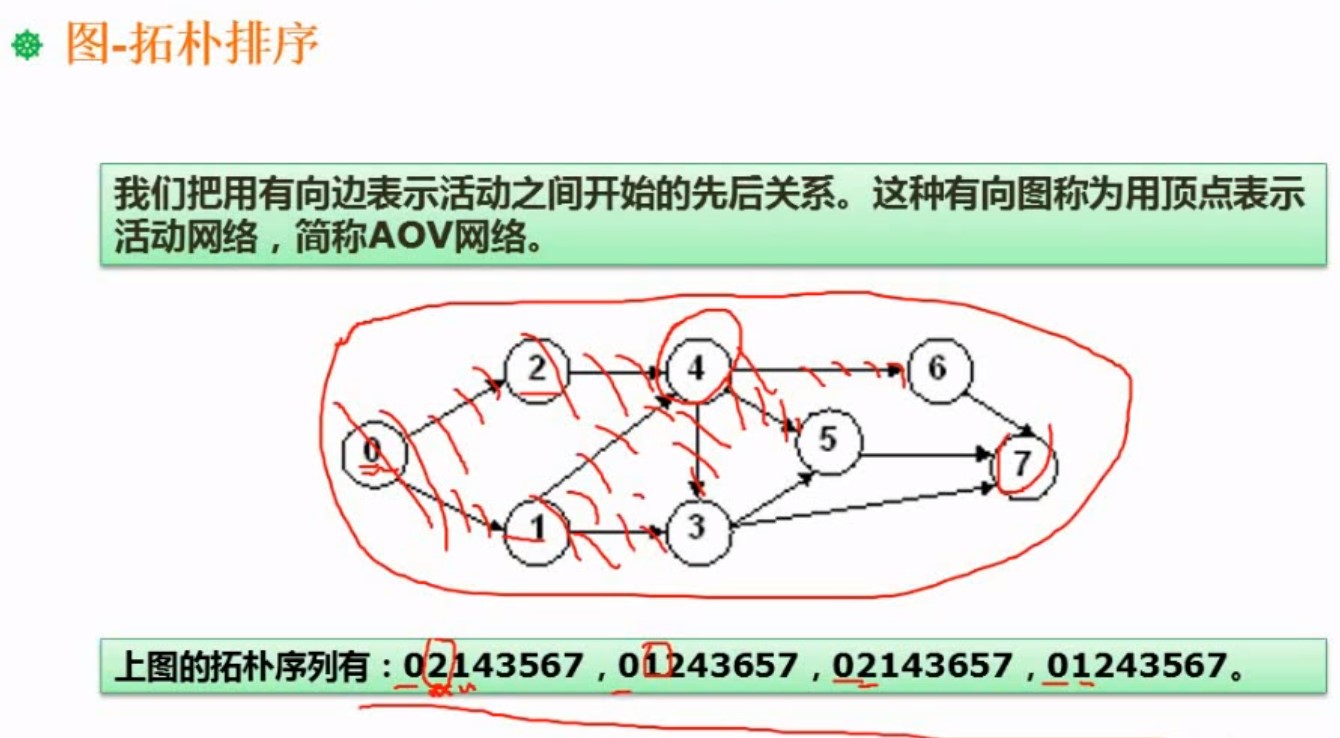
5.3拓扑排序(AOV网络) （重点）

拓扑关系就是哪些时间可以线执行，哪些事件可以后执行

没有箭头指向它，说明没有可以约束他的点

做这个题就是哪个点可以先执行，哪个点需要等后面的才能执行，拓扑序列一般不只一条

一般考试问的是，下面哪个不是拓扑序列的排序

5.4图的最小生成树

这个就是把图的一些边去掉，保留几条边，满足将所有的节点连起来，留下来的边权值小，所以相加起来就会小很多

树和图的最大区别是树没有环路

一个数的节点是n，树的边最多是n-1，如果小于n-1,说明形成了环路，变成了图     

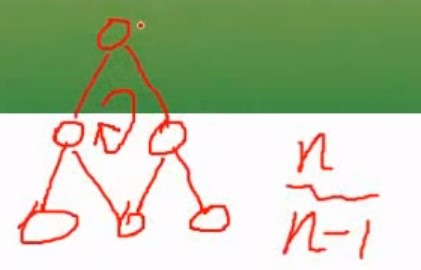
所以就是转为最小生成树，是看多少个节点，选出 n-1条边，来形成树，其余的边去掉，选的边不能形成环路，有环路就不是树了

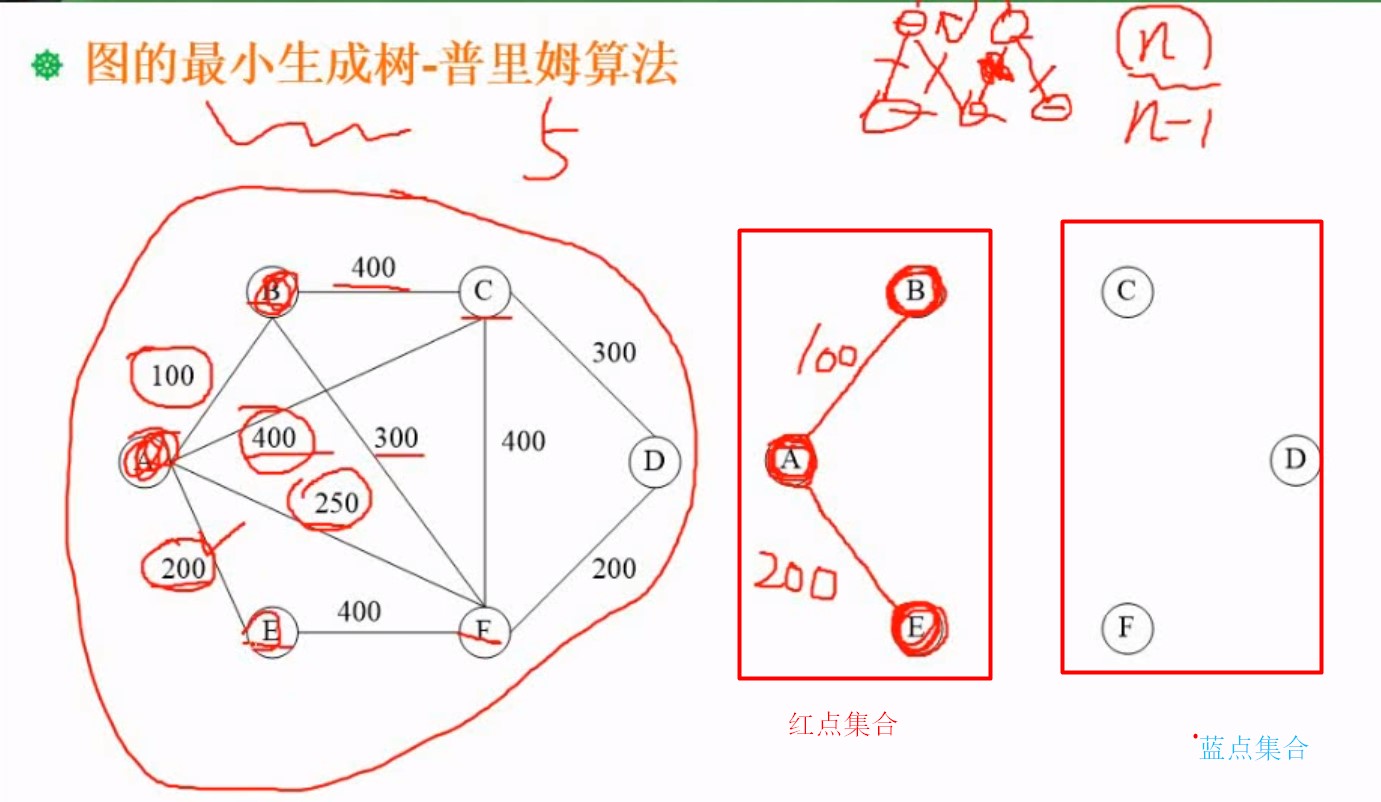
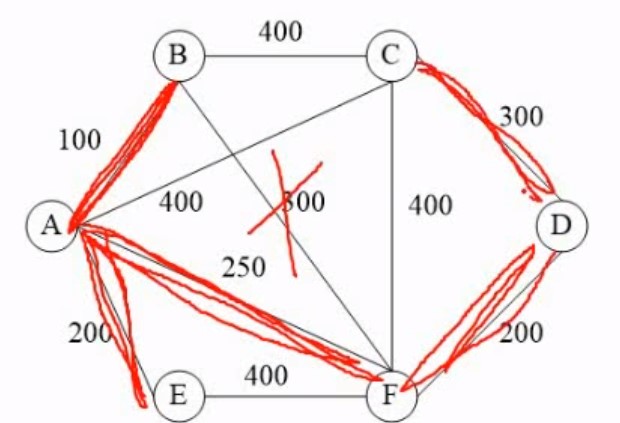
5.4.1Prim(普里姆)算法

网密，prim好，效率高

就是看情况(一般从左到右)再找一个节点开始，这个节点作为红点集，接着剩下的部分作为蓝点集

然后看图，算红点集到蓝点集，最短的是那个边，让然后链接起来，连接起来的点，也是属于红点集了

接着继续算红点集到蓝点集，最短的边，以此类推 选的边不能形成环路，有环路就不是树了

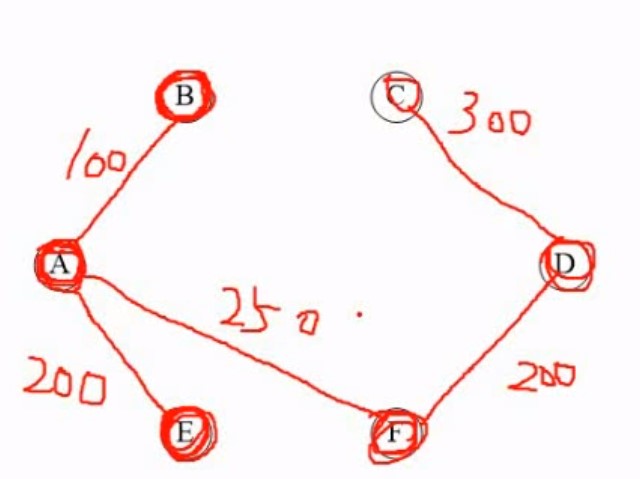
5.4.2Kruskal(克鲁斯卡尔)算法

就是先确定选多少条边，接着选最小的边，接着又选最小的边，慢慢的链接起来即可

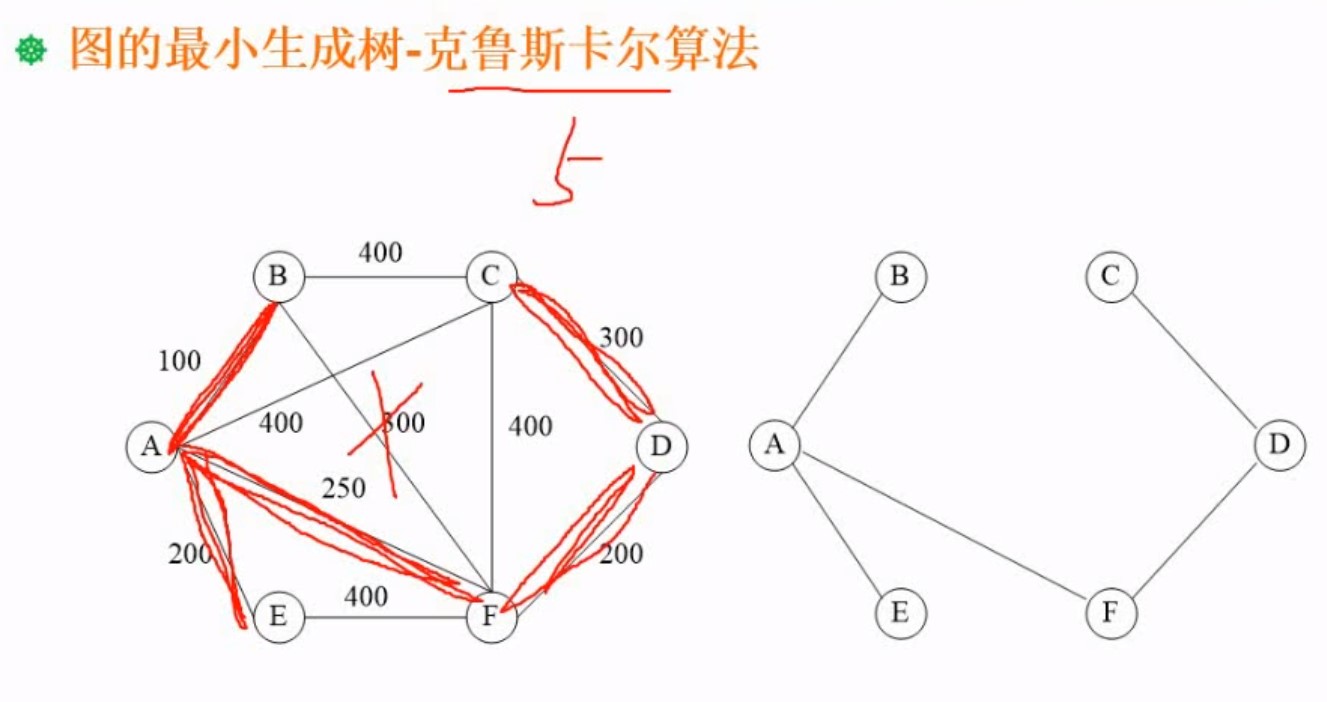
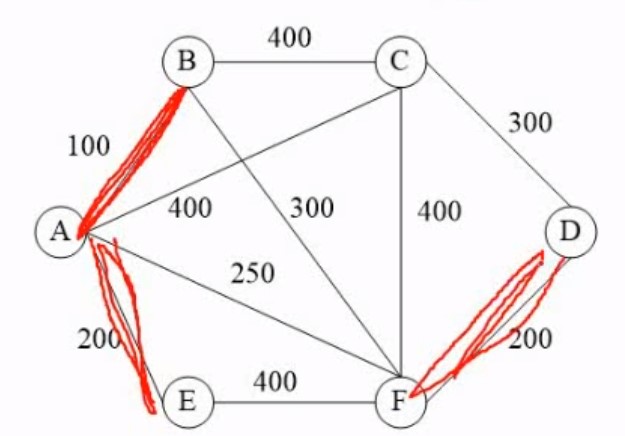
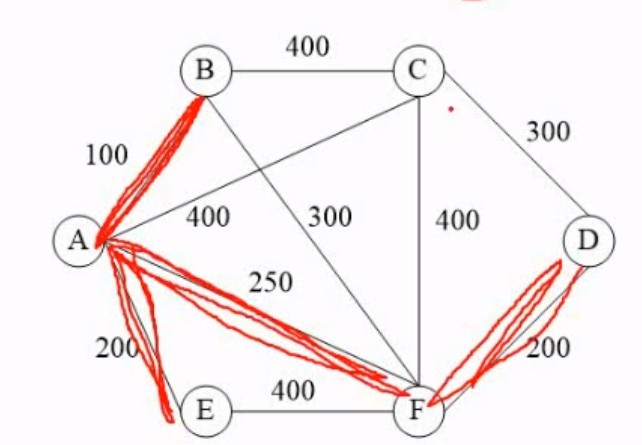
6.算法基础

6.1算法特点

• 有穷性，就是可以在有限顺序完成，不能是无穷的      --步骤的数量
• 确定性，例如随机函数，不仅仅是我们自己输入的数，还有算法获取系统的数据作为输入
• 输出的结果肯定要大于1个 
• 有效性，就是每个步骤能输出一个有效的结果  

6.2算法的复杂度

大概率是下午的题，问设计算法的时间复杂度

时间复杂度是取最高的

• o(1)  就是常数级别的，例如赋值语句  int a = 1;所有常数级的都用o(1)来代表
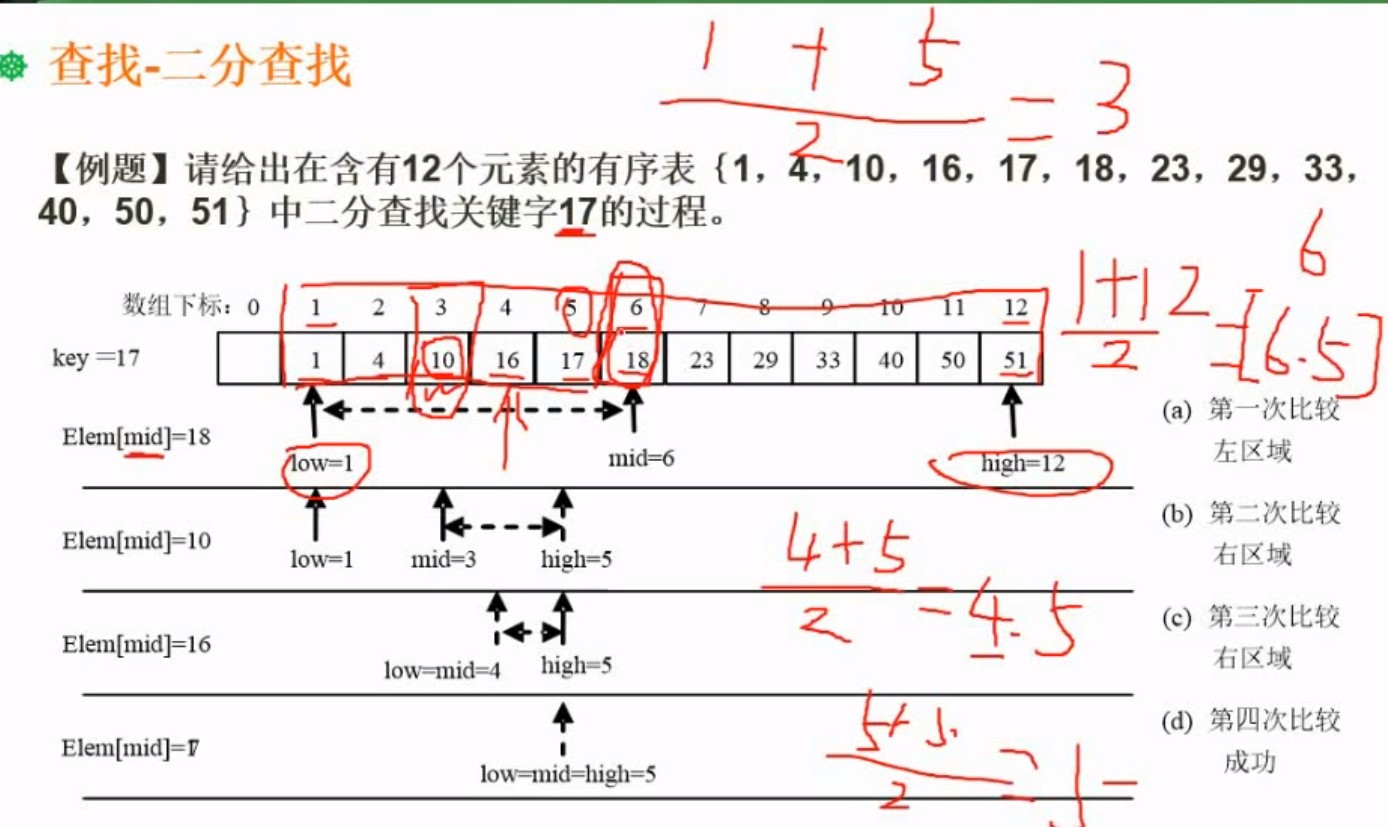
• o(log2n)  是平常用的排序二叉树的折半查找   例如折半查找的就是树多少层，最多比较多少次
• o(n)  常用的就是for循环的遍历n便   

例如三个赋值语句o(3)，接着循环了n次 o(n)，再打印两次o(2),   这些操作的时间复杂度是   o(n)   取最高的 

双重循环 o(n^2)

三重循环 o(n^3)

例如循环层数有2有3，取3    取 o(n^3)

6.3 查找算法

6.3.1顺序查找

6.3.2二分查找

前提是序列已经排好序了

这个是按照分多少层，是按照满二叉树来排，就是要取多少次中间   ，就是最多比较多少次

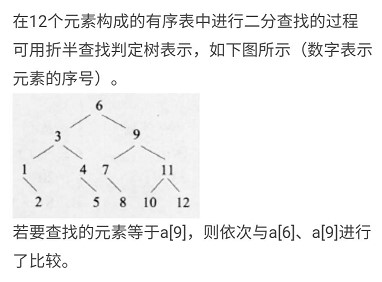
记得二分查找的中间值是取地板的，取整

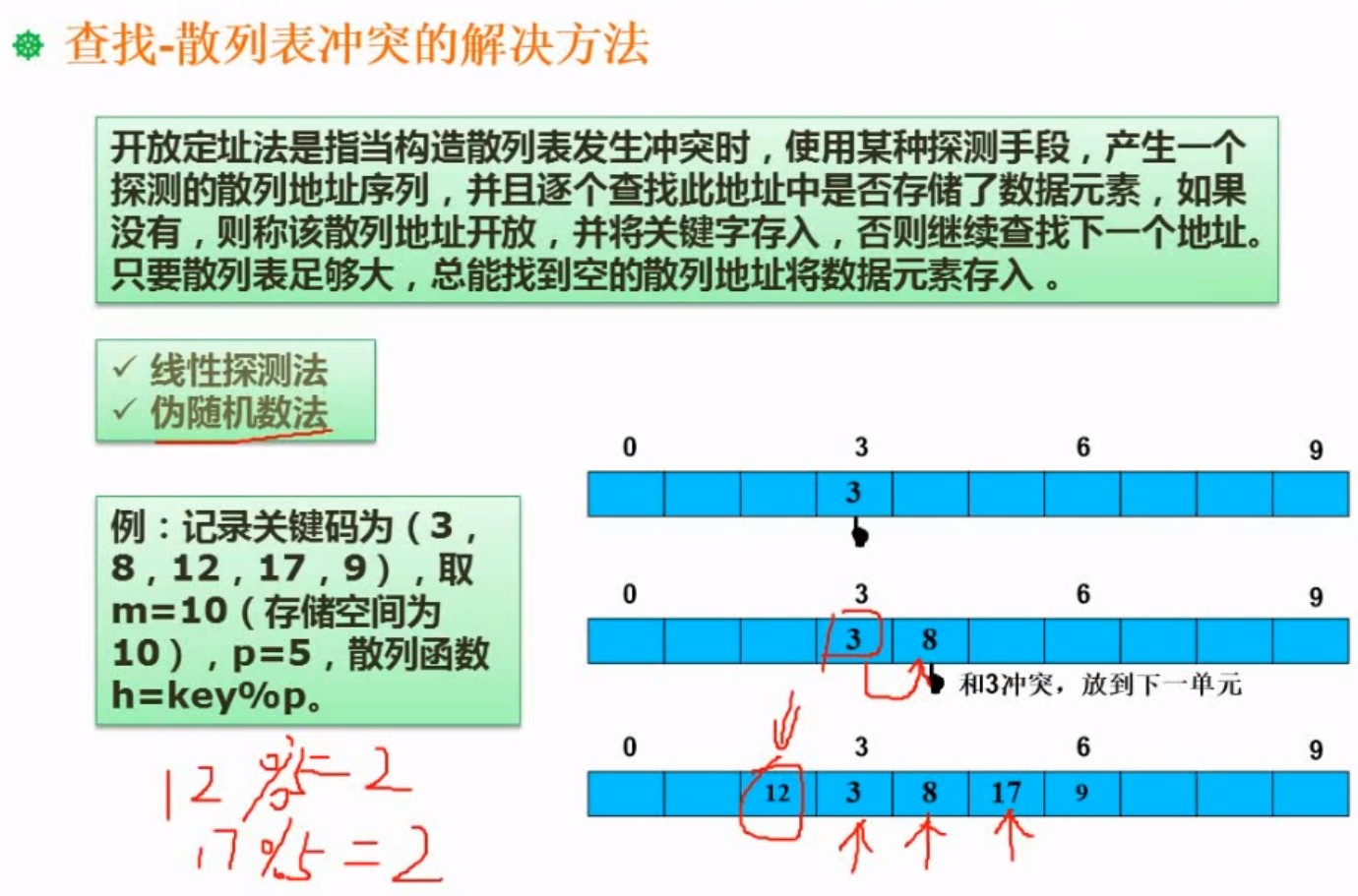
6.3.3 散列表

就是类似哈希表，数组加链表

就是类似按照内容去存储

线性探测法：就是，哈希冲突了，然后将他移动到下一个没有人占用的位置

6.4排序算法

• 稳定排序    例如两个相同的键值的，但是这两个键值还有其他相关联的东西，例如下面的黑21和红21，稳定排序后黑21还是在红21前面
• 不稳定排序   不稳定就是排序后红21会来到黑21前面

• 内排序：内存里面进行排序
• 外排序：外部的存储空间进行排序

快速排序，堆排序考的比较多，其他简单的例如冒泡考的少，还有归并和基数理解概念即可，考的少

6.5插入类排序

• 少数据用直接插入排序
• 多数据先用希尔排序，进行分组，接着再组内进行直接插入排序

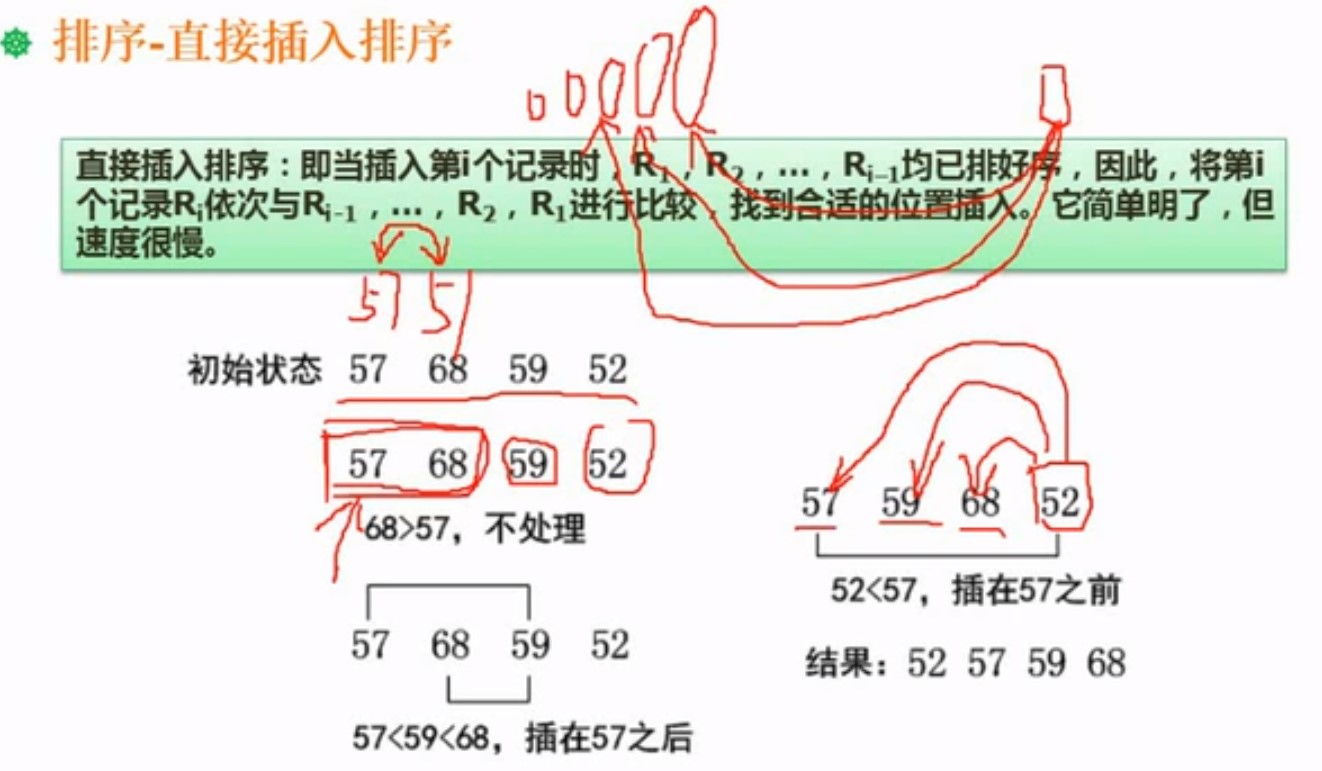
6.5.1直接插入排序

来一个跟前面的进行比较，找到合适的位置插入

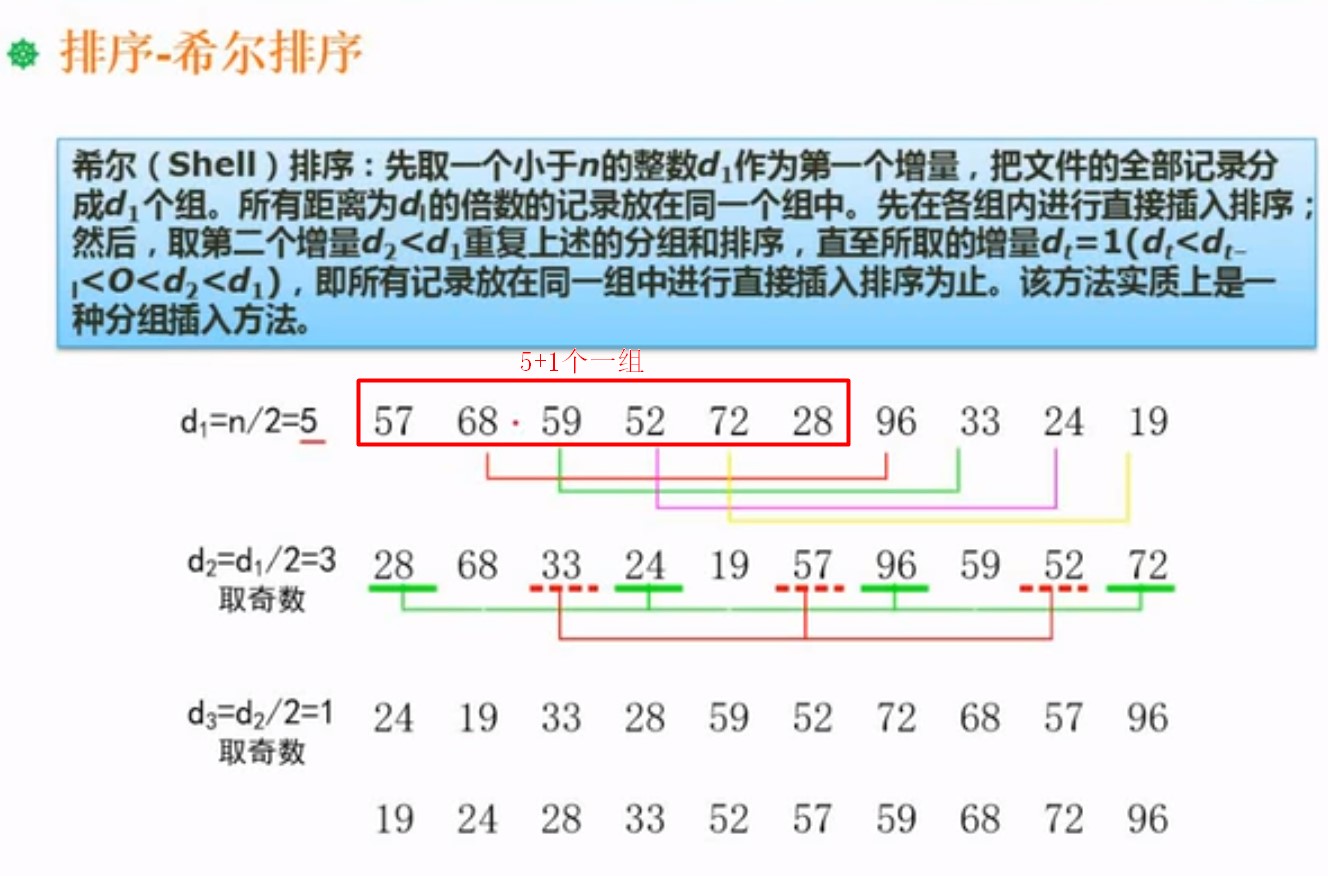
6.5.2.希尔排序

就是首先拿到排序的数量n,然后除 2，取天花板，例如等于4.5，就取5

然后将得到的余数，用在序列里面，相隔多少个，例如上面的 5+1个成为一组，然后组内进行直接插入排序

然后将上一个的结果倍数，再次然后除 2，取天花板，重复操作  直到相隔倍数 等于1 完成排序

6.6 交换类排序

6.6.1 冒泡排序

就是相邻的进行比较，逐渐将最大的冒上去，接着又继续之前的操作，将第二个大的又冒上来

6.6.2 快速排序(复杂)

当基本有序时，是快排最坏情况，是o(n^2)

就是选一个基准，大的全部交换到右边，小的全部分到左边，然后，在分别的左右部分，一样分别选一个基准，进行同样操作

6.7 选择类排序

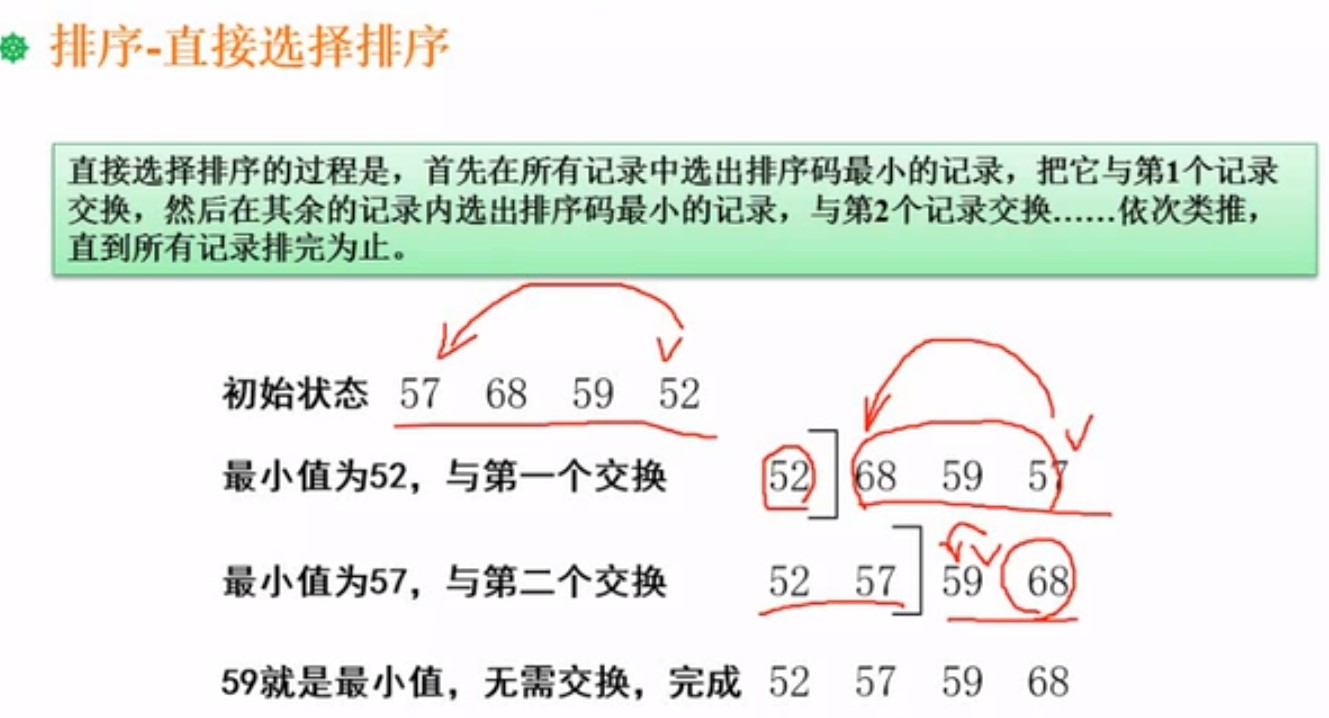
6.7.1 简单选择排序

就是每次选出最小的，然后跟前面的进行交换

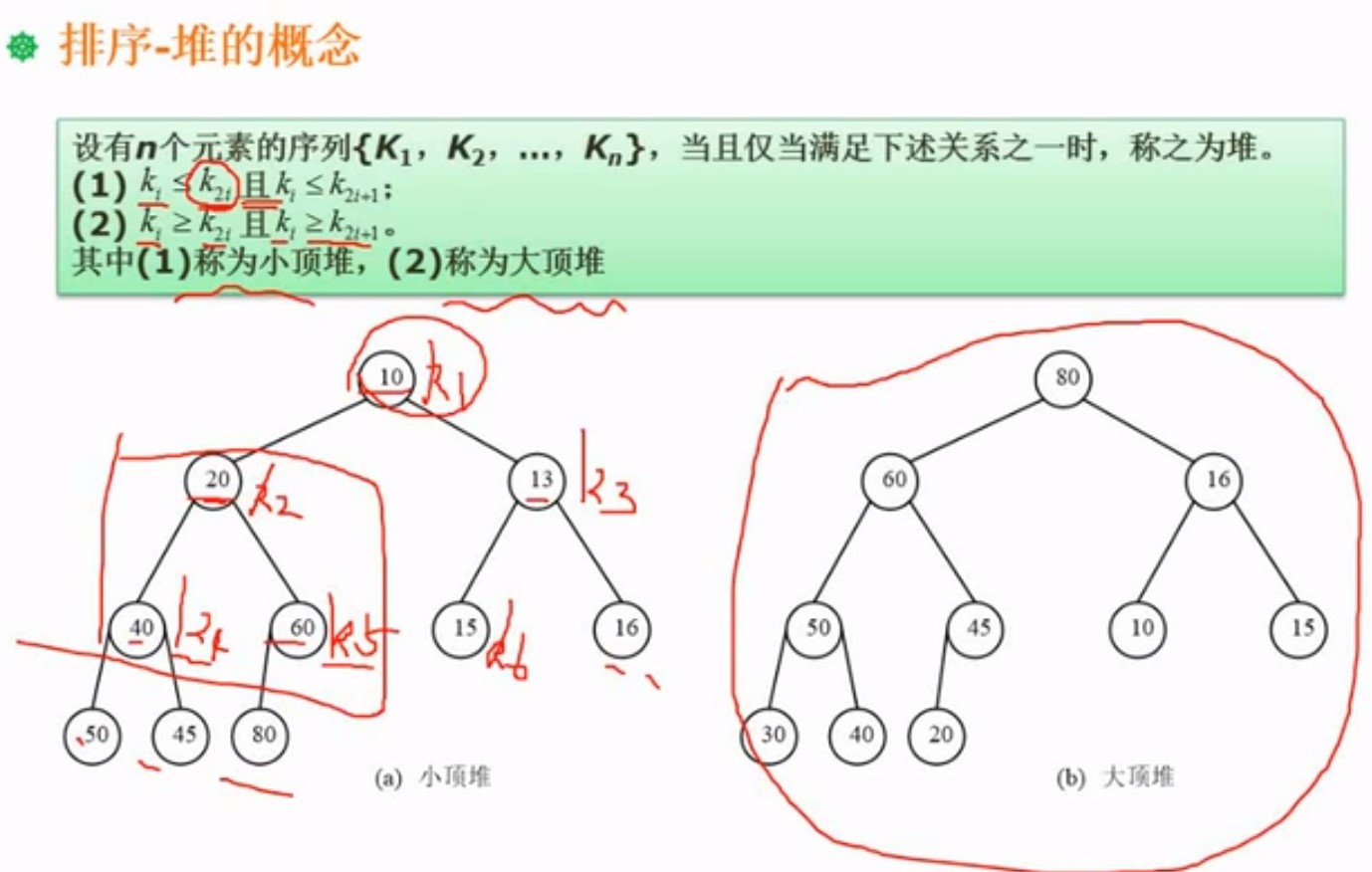
6.7.2 堆排序(复杂)

使用场景最多的就是一堆数据，选出前几名这种，不用给全部数据进行排序

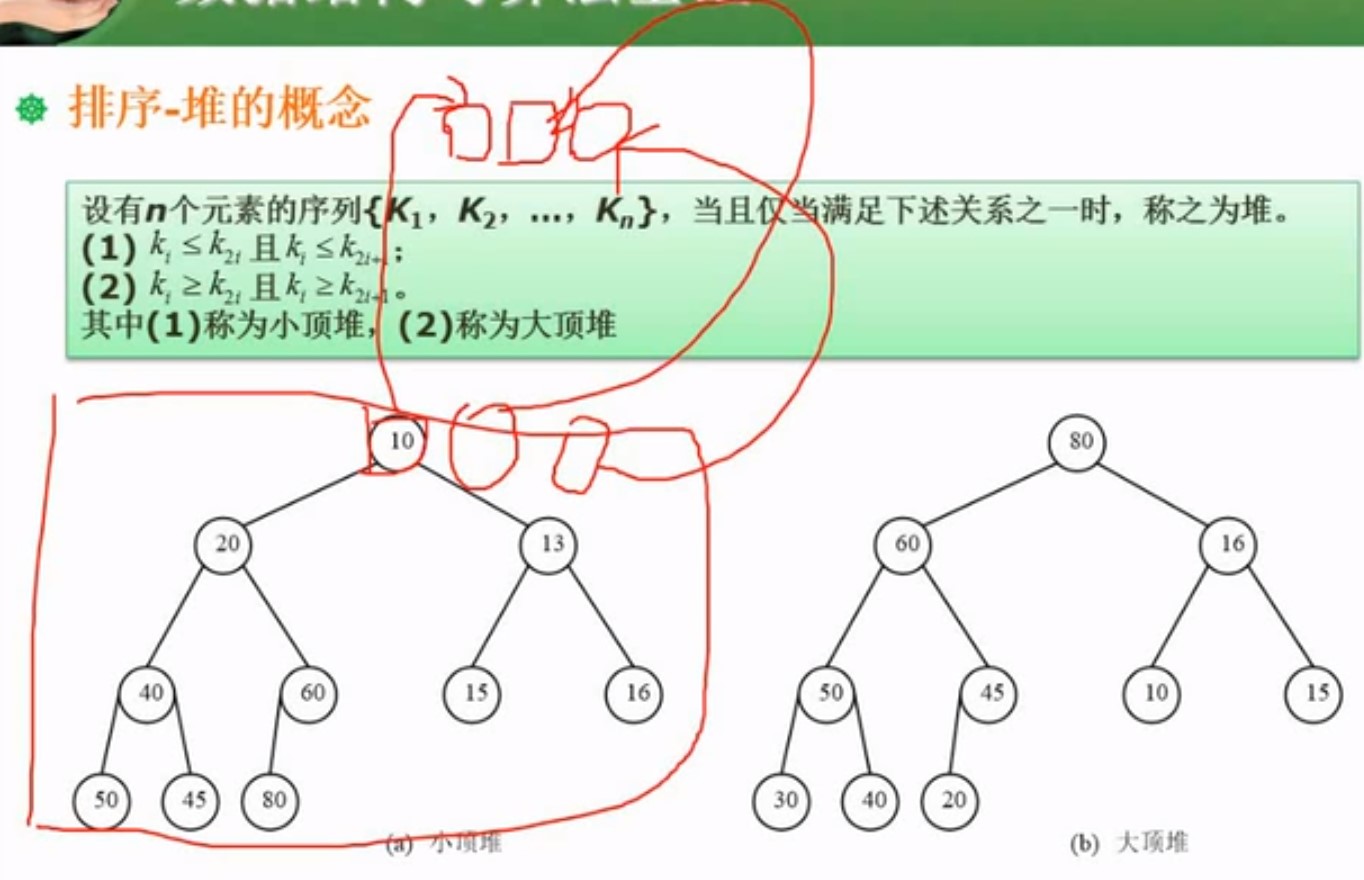
小顶堆：所有子节点大于父节点

大顶堆：所有子节点小于父节点

思路就是将数据排成堆，取走顶点，剩余的节点，重组堆，再取堆顶，再重建，以此类推

初建堆

将数组，按照平衡二叉树(从上倒下，从左到右)来排列，接着按照平衡二叉树(从上倒下，从左到右)的方式，取最后一个非叶子节点的节点

如下图，5是最后一个非叶子节点的节点

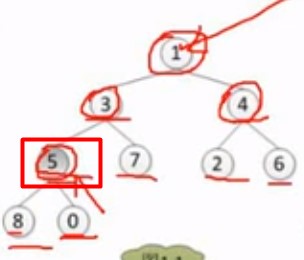
下面是按照建立大顶堆的方式，看节点是否大于子节点，如果不大，就要进行调整，跟子节点进行交换  ，每次交换跟最大的进行交换

接着又到上一个非叶子节点的判断，以此类推，当将子节点进行交换时，如果交换后，发现交换的节点出现，不是最大的节点

所有又要进行大顶堆的调节

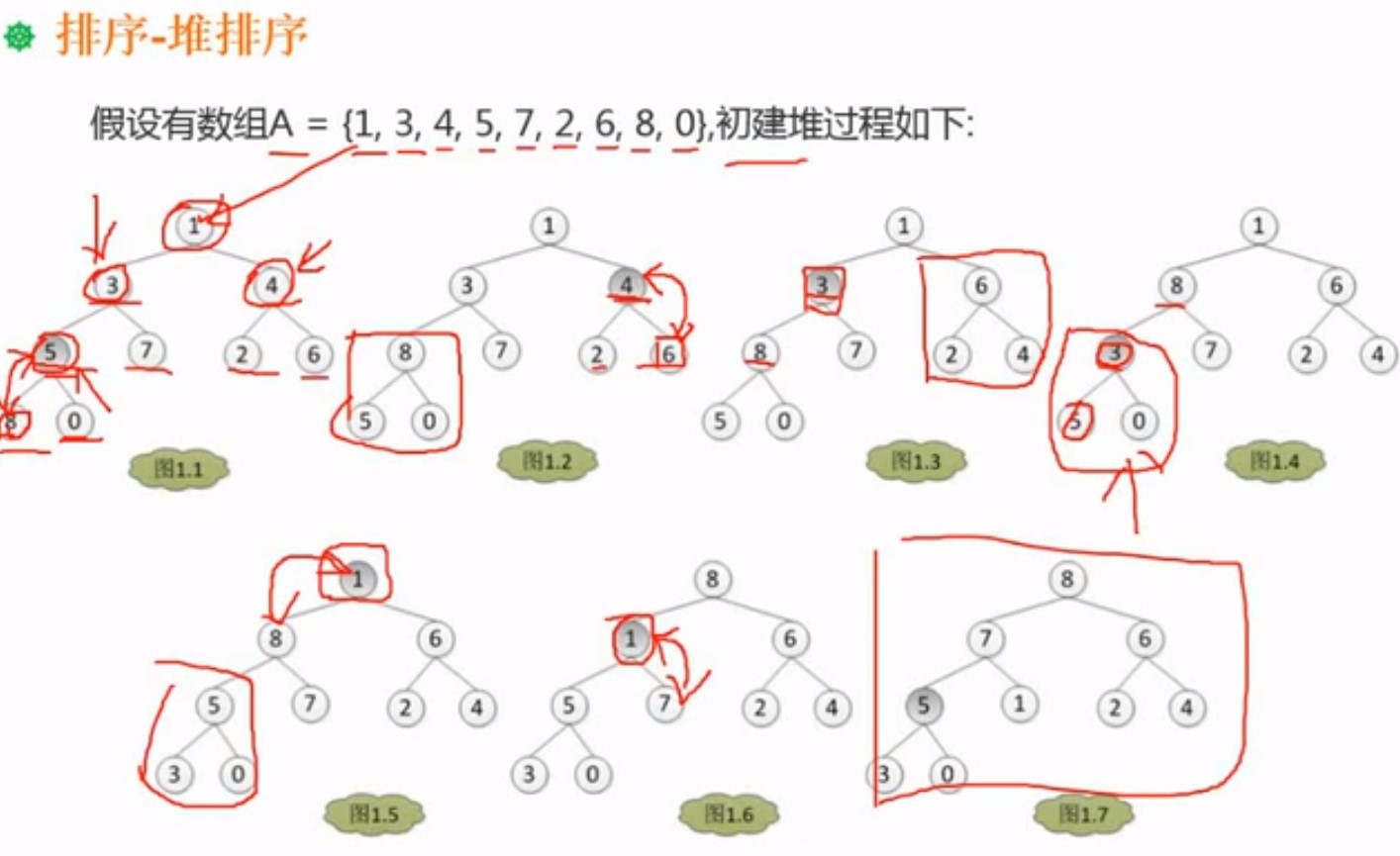
后续的重建堆

将最后节点放到顶节点，然后按照大顶堆的要求，来进行调整捷

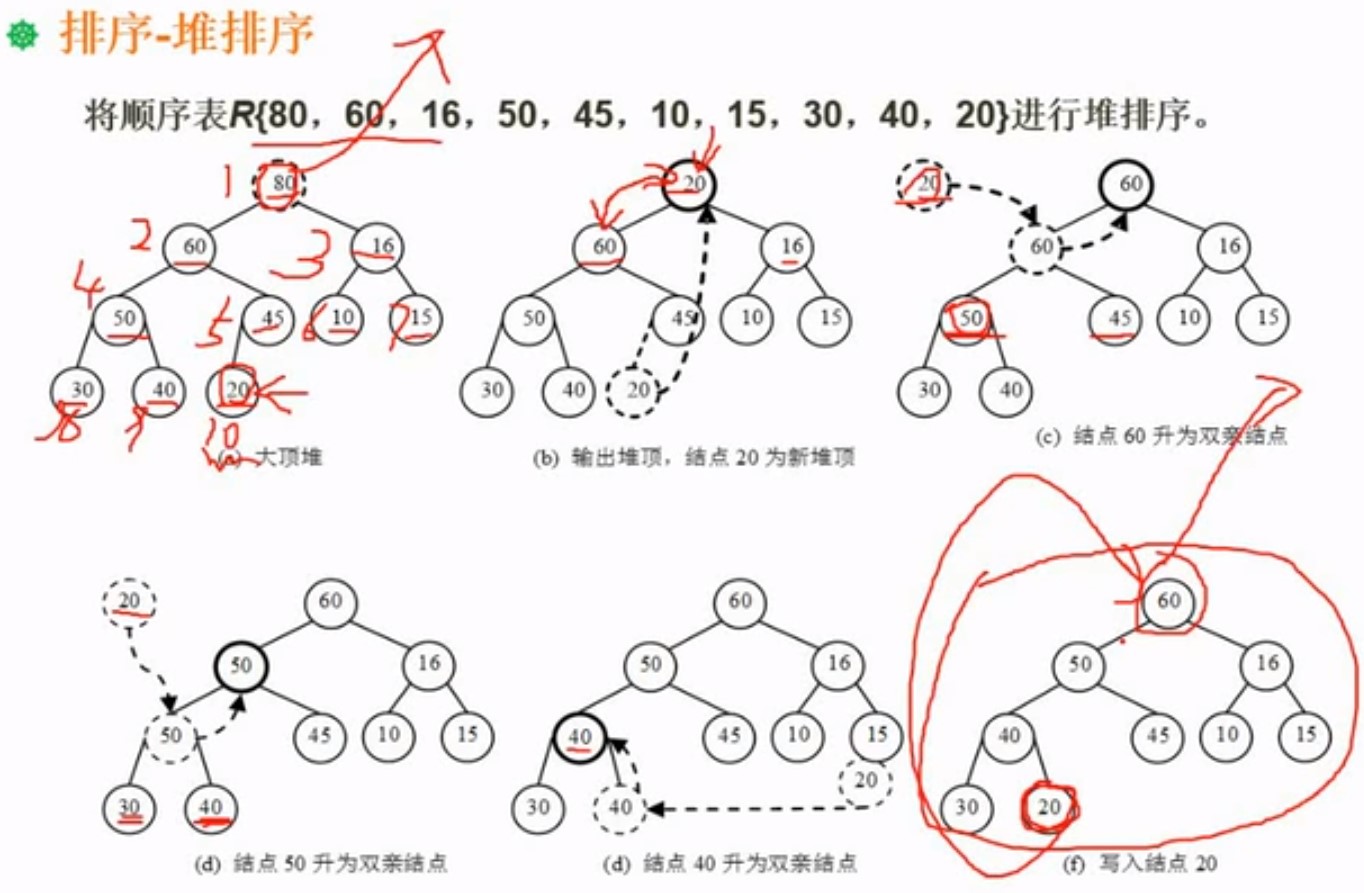
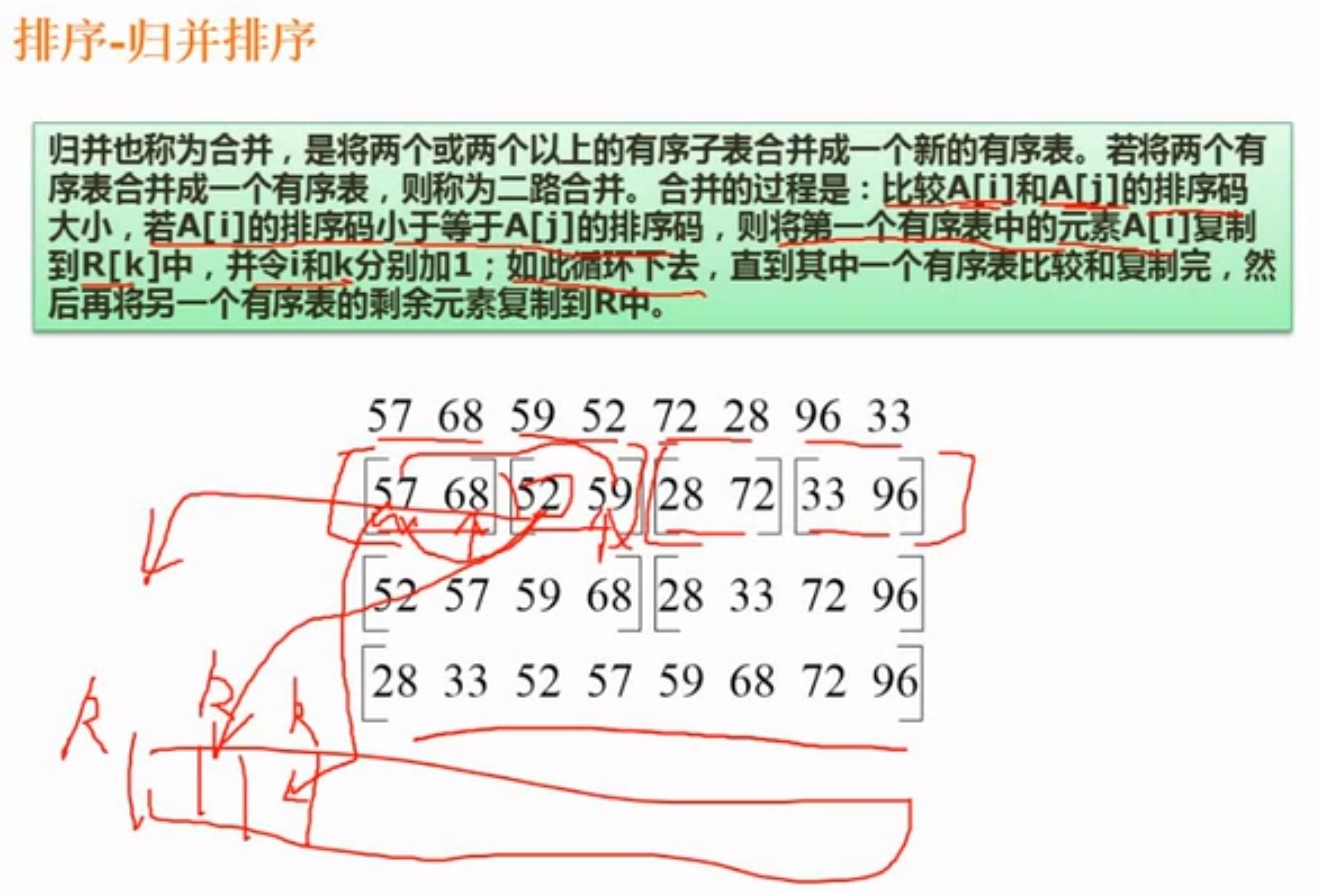
6.8归并排序

就是将元素分别两两分组，然后，组内进行比较交换，接着合并是，组内的第一个和另外一个组的全部元素进行比较，然后交换位置

以此类推。

6.9基数排序

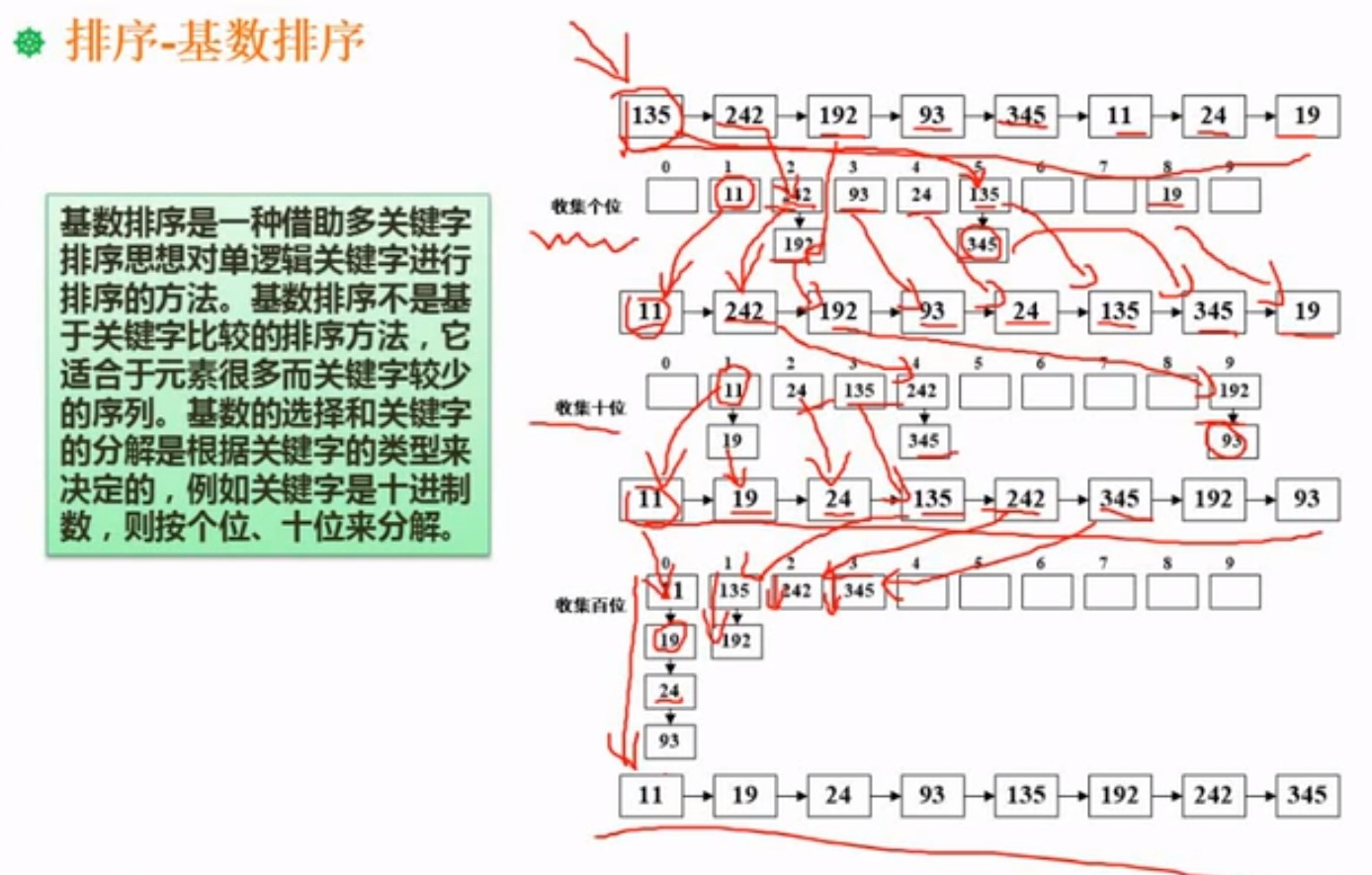
基数排序就是按照个，十，百..来分别进行排序，按照0到9进行排序，将收集到的结果作为新的排序序列

接着在新的排序序列，按照十位进行排序，然后收集，以此类推。

6.10排序算法的总结(必考)

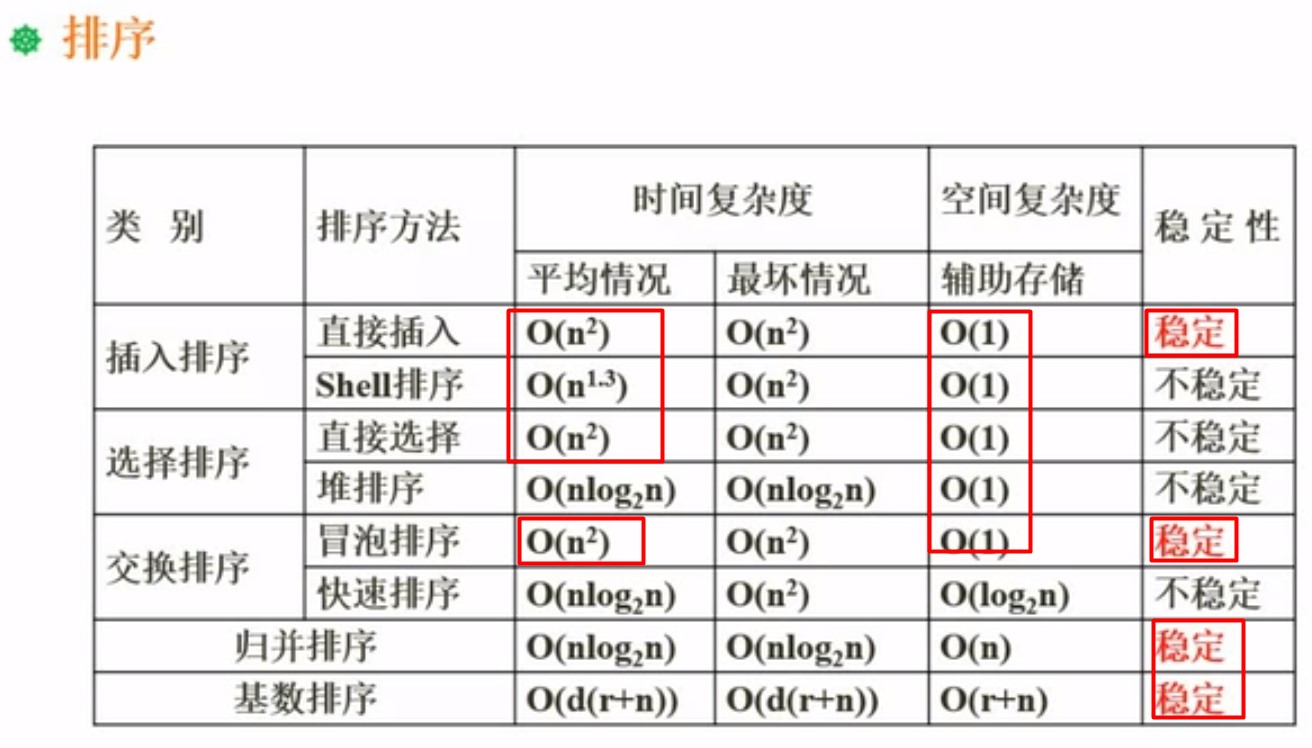
• 插入，冒泡，归并，基数是稳定的
• 绝大部分(基本的6个，除了快排)的空间复杂度是o(1)，归并是o(n) 
• 时间复杂度以o(n^2)为主，复杂排序(快排，堆排)是nlog2n,因为涉及到二分，和数的结构
• 基本有序，用插入，时间复杂度0(n)

来自为知笔记(Wiz)