(1)GAN理论

GAN产生的背景

深化机器对数据的理解能力

近年来，随着人工智能的进一步发展，机器学习也在不断地更新和迭代。一般我们认为人工智能分为两个阶段：认识阶段和感知阶段，其具体的涉及了对数据和事物的判断、生成和理解等，其中最重要的是理解能力，但是，无论对于个人还是机器而言，理解能力都是无法直接测量的，因而我们可以通过机器制造数据的能力进而判断它的理解能力，GAN（Generative Adversarial Networks）能够生成数据样本的特性极有利于深化我们对机器理解数据能力的研究。

对数据的需求

现代计算能力不断提高，机器学习对数据有了更高的要求，我们需要更多、更有效的数据。ML领域有两大类学习方式：监督式学习和非监督式学习，前者是针对不带标签的数据p（标签|数据），后者是针对不带标签的数据p（数据）。自然界中带标签的数据是非常少的，这种标签只对人有意义，如要获得只能通过人力标注，而在人类认识世界的过程中，并不需要给事物都打上标签，在我们打上标签的时候很可能已经对数据产生了破坏，GAN能很好的解决数据的这种问题，一方面，我们能够根据原有的数据生成更加丰富多样的数据，另一方面，我们不需要对数据进行标记。

从机器的角度理解数据

从人的角度理解数据需要我们对数据的显式变量或者隐含变量进行分布假设，之后我们用数据来拟合模型，相反从机器的角度理解数据，我们不需要对数据进行人为的假设，虽然这样产生的模型可能是人类无法理解的，但它所产生的数据样本是我们可以理解的。神经科学理论认为，人类学习源自对周围环境的预测，如果身边的一切事物跟预想的一样规律运作，学习就不会发生；如果所预测的运作与观测不符，学习就会发生。

机器学习——生成模型和判别模型

机器学习的两大模型是生成模型和判别模型，机器学习一直集中在判别模型，原因是判别模型的损失函数loss方便定义，而生成模型的loss却很难定义，近些年提出的神经网络变种有上百种，但损失函数却寥寥无几。 在没有标签的情况下，我们无法通过标签提供的误差梯度对网络进行训练，必须要通过其他方法定义误差函数以产生误差梯度。这方面的先驱是Hinton提出的Restricted Boltzmann Machine；其他方法还包括 Variational Auto Encoder以及GAN等。GAN将机器学习的两类生成和判别相结合，把生成模型的回馈部分交给判别模型来做。

对抗思想的发展

从机器学习到人工智能，对抗思想被成功引入若干领域并发挥作用。人类做出每一项决策，其实都是与其他若干拥有同样智能的人类相互博弈的过程。博弈、竞争中均包含着对抗的思想，博弈机器学习将博弈论的思想与机器学习结合，这种思想不仅在优化在线广告竞价机制中得到了有效的应用，而且也在社交媒体、众包管理、交通疏导等方面也得到了应用。GAN基于这种思想通过生成器与判别器之间的对抗，实现数据的同分布生成。对抗思想应用于机器学习和人工智能取得的诸多成果，也激发了更多的研究者对GAN的不断挖掘。

 

GAN的主要理论

基本框架

 

 

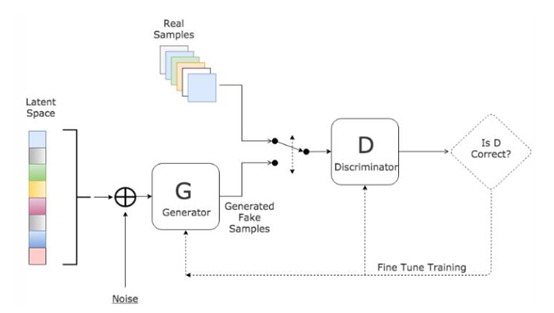
生成器G：尽量去学习真实的数据分布，生成无限接近真实数据的样本

判别器D：尽量去判别输入数据是真实数据还是来自于生成器生成的数据

主要过程为：

1. 输入噪声（隐藏变量）z
2. 通过生成部分G得到$G(z)=x_{fake}$
3. 从真实数据集中取一部分真实数据$x_{real}$
4. 将两者混合$x=x_{fake}+x_{real}$
   
5. 将数据喂入判别部分D，给定标签$label_{fake}=0$,$label_{real}=1$（简单的二类分类器）
6. 按照分类结果，回传loss

生成器与判别器之间存在着对抗，一方面，从生成器而言，希望D(G(z))为1，提高自己的生成能力；另一方面，从判别器而言，希望D(G(z))为0，提高自己的判别能力。经理论证明，两者最终可以达到纳什均衡——处于此状态下，利益达到最大，双方都不愿意改变自己的状态。

理论证明 

    首先，我们在给定生成器的情况下，考虑最优化判别器D。和一般的基于Sigmoid的二分类模型训练一样，训练判别器D也是最小化交叉熵的过程，其损失函数为（二分类）：

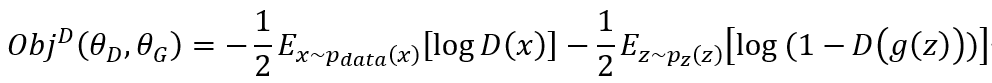
 训练过程就是最小化损失函数的过程，在连续空间上我们进而写成：

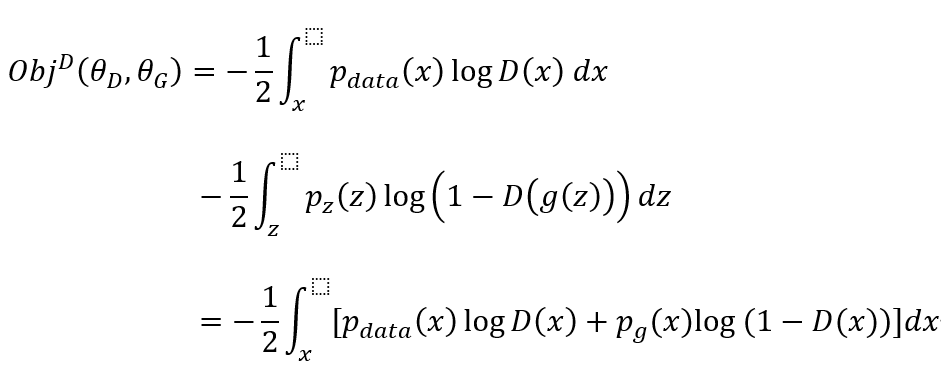
 去除常量-1/2，我们约定质量函数为V（G,D）:

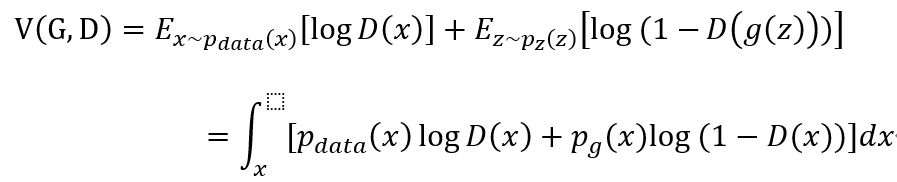
 利用微积分我们求得在给定G的情况下，质量函数在

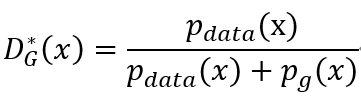
处得到最大值，此即为判别器的最优解。

生成器和判别器是一个对抗的过程，而且是零和博弈，所以生成器的损失函数$Obj^G(\theta_G)=-Obj^G(\theta_G,\theta_D)$,所以GAN的优化问题是极小—极大问题，GAN的目标函数可以描述如下：

 当且仅当$p_{data}=p_g$,时达到全局最优，即$V(G,D^*)$此时取最小值，证明如下：

原论文中的这一定理是「当且仅当」声明，所以我们需要从两个方向证明。

首先我们先从反向逼近并证明（1）式的取值，然后再利用由反向获得的新知识从正向证明。设$p_{data}=p_g$,（反向指预先知道最优条件并做推导），此时$D^*=1/2$我们可以反向推出：

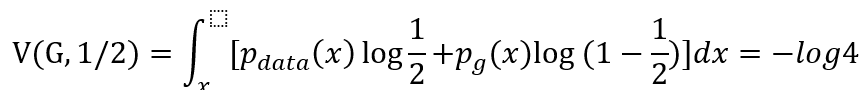
 现在我们来证明这个就是最小值，我们把$D^*$带入质量函数$C(G)=max V(G,D)$:

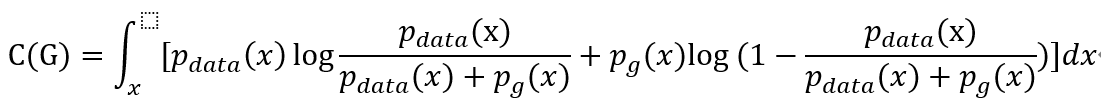
因为已知-log4为全局最小候选值，所以我们希望构造某个值以使方程式中出现log2。因此我们可以在每个积分中加上或减去log2，并乘上概率密度。这是一个十分常见并且不会改变等式的数学证明技巧，因为本质上我们只是在方程加上了0。

采用该技巧主要是希望能够构建成含log2和JS散度的形式，上式化简后可以得到以下表达式：

 

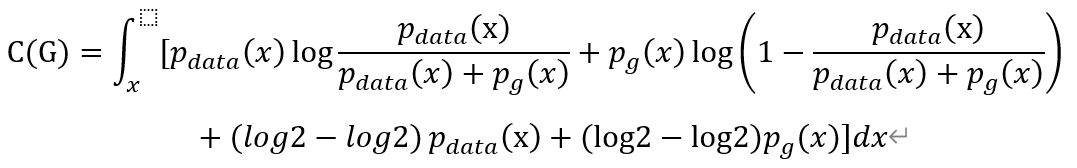
 进而我们写成：

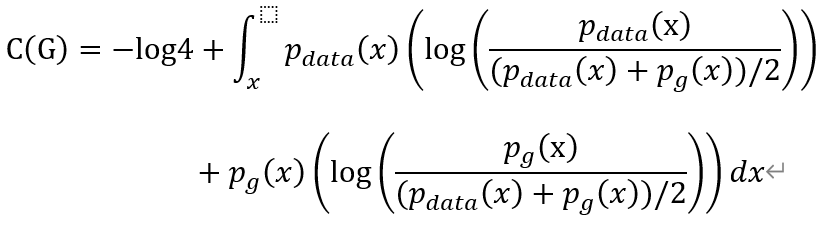
根据散度的有关知识，我们进而写成KL散度的形式：

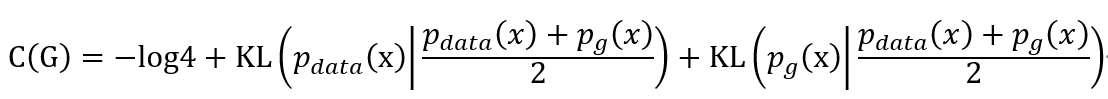
 KL散度是非负的，所以我们可以认为-log4是最小值。

下面我们证明$p_{data}=p_g$是使C(G)取-log4的唯一点。

我们知道：$JSD(P||D)=\frac{1}{2}D(P||M)+\frac{1}{2}D(Q||M)$,其中$M=\frac{1}{2}(P+Q)$,所以：

我们根据JS散度的定义和性质可以知道，当且仅当 时，JS散度取零，C(G)取-log4。

综上所述，当且仅当 时，我们得到最优生成器。

模型训练过程

先训练判别器使判别器达到最优，再训练生成器使二者完成对抗优化，最终达到$p_{data}=p_g$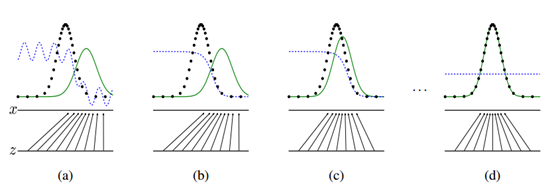

 

 如上图所示，生成对抗网络会训练并更新判别分布（即 D，蓝色的虚线），更新判别器后就能将数据真实分布（黑点组成的线）从生成分布（绿色实线）中判别出来。下方的水平线代表采样域Z，其中等距线表示Z中的样本为均匀分布，上方的水平线代表真实数据X中的一部分。向上的箭头表示映射 x=G(z) 如何对噪声样本（均匀采样）施加一个不均匀的分布$p_g$.

（a）考虑在收敛点附近的对抗训练:$p_g$和$p_{data}$已经十分相似，D是一个局部准确的分类器。

（b）在算法内部循环中训练 D 以从数据中判别出真实样本，该循环最终会收敛到

（c）随后固定判别器并训练生成器，在更新G之后，D的梯度会引导G（z）流向更可能D分类为真实数据的方向。

（d）经过若干次训练后，如果G和D有足够的复杂度，那么它们就会到达一个均衡点。这个时候$p_{data}=p_g$，即生成器的概率密度函数等于真实数据的概率密度函数，也即生成的数据和真实数据是一样的。在均衡点上D和G都不能得到进一步提升，并且判别器无法判断数据到底是来自真实样本还是伪造的数据，即D（x）= 1/2。

 

 

 

西工大陈飞宇还在成长，如有错误还请批评指教。