数据结构与算法——查找算法

查找

又称检索或查询，是指在查找表中找出满足一定条件的结点或记录对应的操作。

查找表

在计算机中，是指被查找的数据对象是由同一类型的记录构成的集合，如顺序表， 链表、二叉树和哈希表等

查找效率

查找算法中的基本运算是通过记录的关键字与给定值进行比较，所以查找的效率 同常取决于比较所花的时间，而时间取决于比较的次数。通常以关键字与给定值进行比较的记录 个数的平均值来计算。

查找操作及分类

操作

1. 查找某个“特定的”数据元素是否存在在查找表中
2. 某个“特定的”数据元素的各种属性
3. 在查找表中插入一个数据元素
4. 从查找表中删除某个数据元素

分类

• 若对查找表只进行（1） 或（2）两种操作，则称此类查找表为静态查找表。
• 若在查找过程中同时插入查找表中存在的数据元素，或者从查找表中删除已存在的 某个数据元素，则称此类查找表为动态查找表。

 

1. 数组和索引

日常生活中，经常会在电话号码簿中查阅“某人”的电话号码，按姓查询或者按字母排 序查询；

在字典中查阅“某个词”的读音和含义等等。

这里，“电话号码簿” 和 “字典” 都可 看作一张查找表， 而按 “姓” 或者 “字母” 查询则是按索引查询！

索引把线性表分成若干块，每一块中的元素存储顺序是任意的，但是块与块间必须按关键字 大小按顺序排列。即前一块中的最大关键字值小于后一块中的最小关键字值。

分块以后，为了快速定义块，还需要建立一个索引表，索引表中的一项对应于线性表中的一 块，索引项由键域和链域组成。键域存放相应关键字的键值，链域存放指向本块第一个节点和最 后一个节点的指针，索引表按关键字由小到大的顺序排列！

 

数组是特殊的块索引（一个块一个元素）：

 

哈希表是非常经典的块索引：

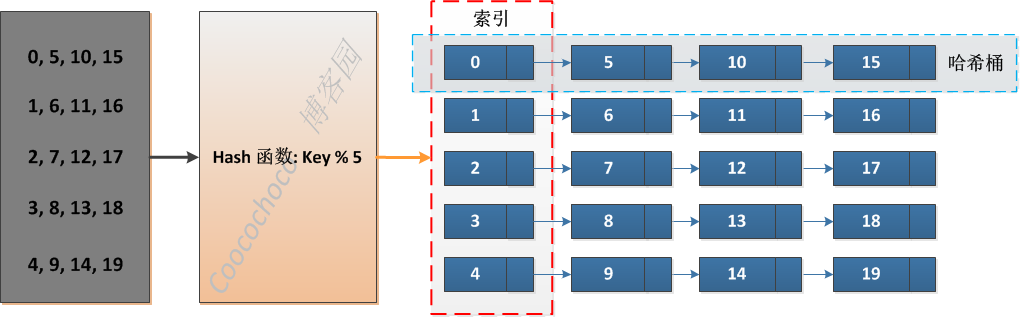
 分块查找的算法分两步进行，首先确定所查找的节点属于哪一块，即在索引表中查找其所在的块， 然后在块内查找待查询的数据。由于索引表是递增有序的，可采用二分查找，而块内元素是无序 的，只能采用顺序查找。（块内元素较少，则不会对执行速度有太大的影响）

 

2. 二分查找

二分查找法实质上是不断地将有序数据集进行对半分割，并检查每个分区的中间元素。再重 复根据中间数确定目标范围并递归实行对半分割，直到中间数等于待查找的值或是目标数不在搜 索范围之内！

#include <stdlib.h>
#include <stdio.h>

int int_compare(const void *key1, const void *key2)
{
    const int *ch1 = (const int *)key1;
    const int *ch2 = (const int *)key2;
    return (*ch1-*ch2);
}

int char_compare(const void *key1, const void *key2)
{
    const char *ch1 = (const char *)key1;
    const char *ch2 = (const char *)key2;
    return (*ch1-*ch2);
}

int BinarySearch(void *sorted, int len, int elemSize, void *search, int(*compare)(const void *key1, const void *key2))
{
    int left = 0, right = 0, middle = 0;
    /*初始化 left 和 right 为边界值*/
    left = 0;
    right = len - 1;
    /*循环查找，直到左右两个边界重合*/
    
    while(left <= right)
    {
        int ret = 0;
        middle = (left + right) /2 ;
        ret = compare((char *)sorted+(elemSize*middle), search);
        
        if(ret == 0)
        {
            /*middle 等于目标值*/
            /*返回目标的索引值 middle*/
            return middle;
        }
        else if( ret > 0)
        {
            /*middle 大于目标值*/
            /*移动到 middle 的左半区查找*/
            right = middle - 1;
        }
        else 
        {
            /*middle 小于目标值*/
            /*移动到 middle 的右半区查找*/
            left = middle + 1;
        }
    }
    return -1;
}

int main(void)
{
    int arr[]={1, 3, 7, 9, 11};
    int search[] = {-1, 0, 1, 7 , 2, 11, 12};
    printf("整数查找测试开始。。。\n");
    
    for(int i=0; i<sizeof(search)/sizeof(search[0]); i++)
    {
        int index = BinarySearch(arr, sizeof(arr)/sizeof(arr[0]),
        sizeof(int), &search[i], int_compare);
        printf("searching %d, index: %d\n",search[i], index);
    }
    
    char arr1[]={'a','c','d','f','j'};
    char search1[] = {'0', 'a', 'e', 'j' , 'z'};
    printf("\n 字符查找测试开始。。。\n");
    
    for(int i=0; i<sizeof(search1)/sizeof(search1[0]); i++)
    {
        int index = BinarySearch(arr1, sizeof(arr1)/sizeof(arr1[0]),
        sizeof(char), &search1[i], char_compare);
        printf("searching %c, index: %d\n",search1[i], index);
    }
    
    system("pause");
    
    return 0;
}

 

 

3. 穷举搜索

有 20 枚硬币，可能包括 4 种类型：1 元、5 角、1 角和 5 分。

已知 20 枚硬币的总价值为 10 元，求各种硬币的数量。

例如：4、11、5、0 就是一种方案。而 8、2、10、 0 是另一个可能的方案，显然方案并不是 唯一的，请编写程序求出类似这样的不同的方案一共有多少种？

（1）编程思路。 直接对四种类型的硬币的个数进行穷举。其中，1 元最多 10 枚、5 角最多 20 枚、1 角最多 20 枚、5 分最多 20 枚。

如果以元为单位，则 5 角、1 角、5 分会化成浮点型数据，容易计算出错。可以将 1 元、5 角、1 角、5 分变成 100 分、50 分、10 分和 5 分，从而全部采用整型数据处理。

#include <iostream>

using namespace std;

int main(void)
{
    int a100 = 0;            //1 元的硬币数量
    int a50 = 0;            //5 角的硬币数量
    int a10 = 0;            //1 角的硬币数量
    int a5 = 0;                //5 分的硬币数量
    int cnt = 0;            //记录可行的方案的种数
    for(a100=0; a100<=10; a100++)
    {
        for(a50=0; a50<=20; a50++)
        {
            for(a10=0; a10<=20; a10++)
            {
                for(a5=0; a5<=20; a5++)
                {
                    if((a100*100 + a50*50 + a10*10 + a5*5)==1000 && (a100 + a50 + a10 + a5)==20)
                    {
                        cout<<a100<<" , "<<a50<<" , "<<a10<<" ,    "<<a5<<endl;
                        cnt++;
                    }
                }//a5 end.
            }//a10 end.
        }//a50 end.
    }//a100 end.
    
    cout<<"可行的解决方案总共有: "<<cnt<<endl;
    
    system("pause");
    
    return 0;
}

穷举法（枚举法）的基本思想是：列举出所有可能的情况，逐个判断有哪些是符合问题所要求 的条件，从而得到问题的全部解答。 它利用计算机运算速度快、精确度高的特点，对要解决问题的所有可能情况，一个不漏地进行检 查，从中找出符合要求的答案。

用穷举算法解决问题，通常可以从两个方面进行分析：

（1）问题所涉及的情况：问题所涉及的情况有哪些，情况的种数必须可以确定。把它描述 出来。应用穷举时对问题所涉及的有限种情形必须一一列举，既不能重复，也不能遗漏。重复列 举直接引发增解，影响解的准确性；而列举的遗漏可能导致问题解的遗漏。 （2）答案需要满足的条件：分析出来的这些情况，需要满足什么条件，才成为问题的答案。 把这些条件描述出来。

 

 

4. 并行搜索

假设我们要从很大的一个无序的数据集中进行搜索，假设我们的机器可以一次性容纳这么多 数据。从理论上讲，对于无序数据，如果不考虑排序，已经很难从算法层面优化了。而利用并行处理思想，我们可以很轻松地将检索效率提升多倍。具体实现思路如下:

将数据分成 N 个块，每个块由一个 线程来并行搜索。

 

线程演示代码：

#include <Windows.h>
#include <stdio.h>
#include <iostream>
#include <time.h>

#define TEST_SIZE (1024*1024*200)
#define NUMBER 20

DWORD WINAPI ThreadProc(void *lpParam)
{
    for(int i=0; i<5; i++)
    {
        printf("进程老爸，我来了！\n");
        Sleep(1000);
    }
    return 0;
}

int main(void)
{
    DWORD threadID1;//线程 1 的身份证
    HANDLE hThread1;//线程 1 的句柄
    DWORD threadID2;//线程 2 的身份证
    HANDLE hThread2;//线程 2 的句柄
    
    printf("创建线程... ... \n");
    
    //创建线程 1
    hThread1 = CreateThread(NULL, 0, ThreadProc, NULL, 0, &threadID1);
    
    //创建线程 2
    hThread2 = CreateThread(NULL, 0, ThreadProc, NULL, 0, &threadID2);
    
    WaitForSingleObject(hThread1, INFINITE);
    WaitForSingleObject(hThread2, INFINITE);
    
    printf("进程老爸欢迎线程归来！\n");
    
    system("pause");
    
    return 0;
}

 

完整代码:

#include <Windows.h>
#include <stdio.h>
#include <iostream>
#include <time.h>

#define TEST_SIZE (1024*1024*200)
#define NUMBER 20

typedef struct _search
{
    int *data;//搜索的数据集
    size_t start; //搜索的开始位置
    size_t end; //搜索的终止位置
    size_t count; //搜索结果
}search;

DWORD WINAPI ThreadProc(void *lpParam)
{
    search *s = (search*)lpParam;
    time_t start, end;
    
    printf("新的线程开始执行...\n");
    
    time(&start);
    for(int j=0; j<10; j++)
    {
        for(size_t i=s->start; i<=s->end; i++)
        {
            if(s->data[i] == NUMBER)
            {
                s->count++;
            }
        }
    }
    
    time(&end);
    
    printf("查找数据所花时间: %lld\n", end-start);
    
    return 0;
}

int main02(void)
{
    int *data = NULL;
    int count = 0;                    //记录的数量
    int mid = 0;
    search s1, s2;
    data = new int[TEST_SIZE];
    
    for(int i=0; i<TEST_SIZE; i++)
    {
        data[i] = i;
    }
    
    mid = TEST_SIZE/2;
    s1.data = data;
    s1.start = 0;
    s1.end = mid;
    s1.count = 0;
    s2.data = data;
    s2.start = mid+1;
    s2.end = TEST_SIZE-1;
    s2.count = 0;
    
    DWORD threadID1;//线程 1 的身份证
    HANDLE hThread1;//线程 1 的句柄
    DWORD threadID2;//线程 2 的身份证
    HANDLE hThread2;//线程 2 的句柄
    
    printf("创建线程... ... \n");
    //创建线程 1
    hThread1 = CreateThread(NULL, 0, ThreadProc, &s1, 0, &threadID1);
    
    //创建线程 2
    hThread2 = CreateThread(NULL, 0, ThreadProc, &s2, 0, &threadID2);
    
    WaitForSingleObject(hThread1, INFINITE);
    WaitForSingleObject(hThread2, INFINITE);
    
    printf("进程老爸欢迎线程归来！count: %d\n", s1.count+s2.count);
    
    system("pause");
    
    return 0;
}
int main(void)
{
    int *data = NULL;
    int count = 0;                    //记录的数量
    data = new int[TEST_SIZE];
    for(int i=0; i<TEST_SIZE; i++)
    {
        data[i] = i;
    }
    time_t start=0, end=0;            //记录开始和结束的时间戳
    time(&start);
    for(int j=0; j<10; j++)
    {
        for(int i=0; i<TEST_SIZE; i++)
        {
            if(data[i] == NUMBER)
            {
                count++;
            }
        }
    }
    
    time(&end);
    
    printf("查找数据所花时间: %lld, count: %d\n", end-start, count);
    
    system("pause");
    
    return 0;
}

 

 

 

 

 

=====================================================================================================================