代码随想录day21 | 530.二叉搜索树的最小绝对差 501. 二叉搜索树中的众数 236. 二叉树的最近公共祖先

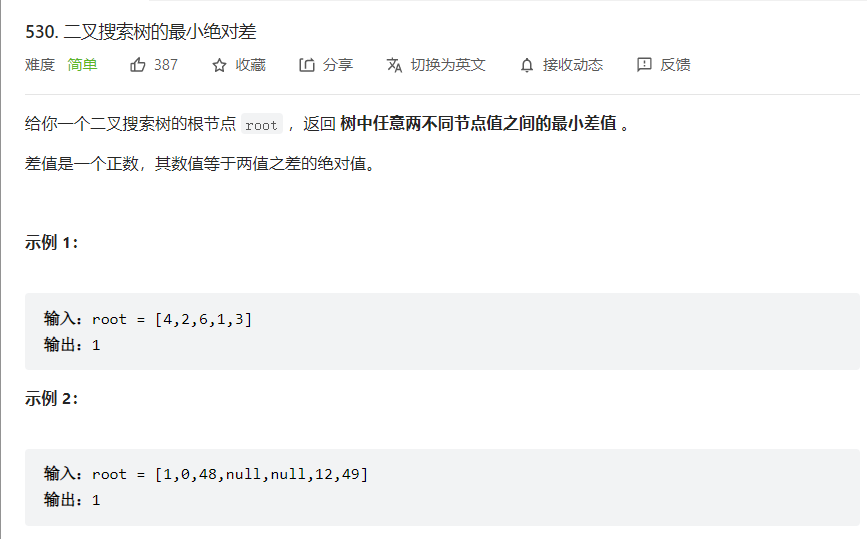
530.二叉搜索树的最小绝对差

题目|文章

思路

1. 二叉搜索树的特点是按照中序遍历从小到大进行排列，因此，按照中序遍历，逐个比较即可找到最小差值
2. 进行中序遍历，当前节点和前一个节点之间的差值小于最小差值时，对最小差值进行更新。

实现

点击查看代码

class Solution {
public:
    int getMinimumDifference(TreeNode* root) {
        traversal(root);
        return min;
    }
    int min = INT32_MAX;
    TreeNode* pre = nullptr;
    void traversal(TreeNode* root){
        if(root->left) traversal(root->left);
        if(pre != nullptr) min = (root->val - pre->val) < min ? (root->val - pre->val) : min; 
        pre = root;
        if(root->right) traversal(root->right);
    }
};

复杂度分析

• 时间复杂度：O(n)，对每一个节点都要进行遍历
• 空间复杂度：O(n)，当二叉搜索树为链表时，空间复杂度为n

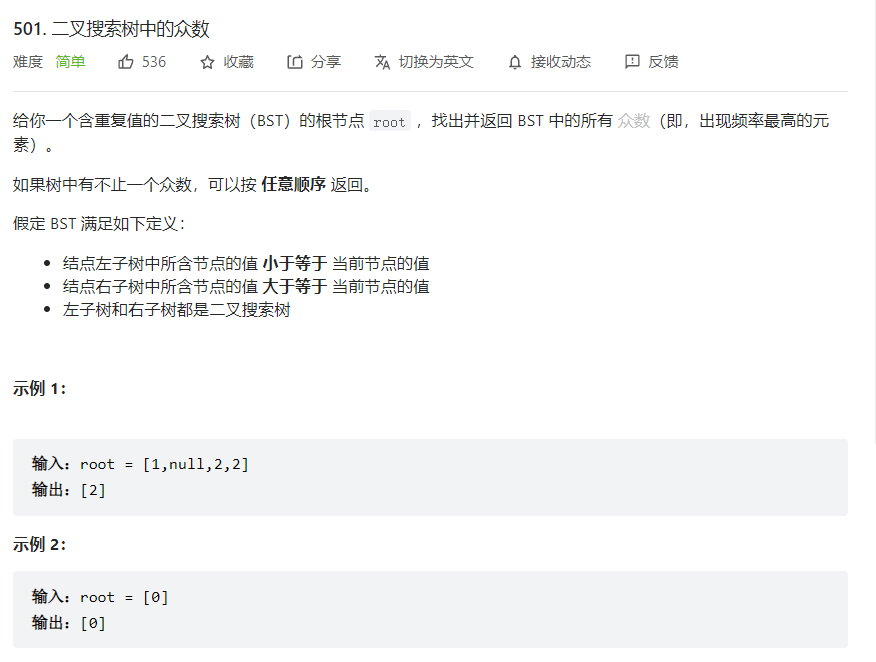
501.二叉搜索树中的众数

题目|文章

1.二叉树中的众数

思路

1.通过map对二叉树的每个数字进行记录，key为值，value为出现的次数
2.map的比较只能比较key值，但不能比较value值，因此，需要重新构造比较函数比较value值。
3.建立一个vector，对map中的键值对进行排序
4.将value最大的key加入到结果中。

实现

点击查看代码

class Solution {
public:
    vector<int> findMode(TreeNode* root) {
        unordered_map<int, int> map;
        traversal(root, map);
        vector<pair<int,int>> vec(map.begin(), map.end());
        sort(vec.begin(), vec.end(), cmp);
        vector<int> result;
        result.push_back(vec[0].first);
        for(int i = 1; i < vec.size(); i++){
            if(vec[i].second == vec[0].second) result.push_back(vec[i].first);
            else break;
        }
        return result;
    }
    void traversal(TreeNode* root, unordered_map<int,int>& map) {
        if(root == nullptr) return;
        map[root->val]++;
        traversal(root->left, map);
        traversal(root->right, map);
    }
    bool static cmp(const pair<int,int>& a, const pair<int, int>& b) {
        return a.second > b.second;
    }
    
    
};

复杂度分析

• 时间复杂度：O(n+logn)，先对二叉树进行遍历，再对结果进行排序
• 空间复杂度：O(n)

2.二叉搜索树的众数

思路

1.利用二叉搜索树的特性进行简化，对出现的的次数进行计数。

• 如果前节点为空，count = 1
• 如果前节点和当前节点的值相等，count++
• 如果前节点和当前节点的值不同，count = 1

2.将count值与max_count值进行比较

• 如果相等，将当前节点的值加入结果
• 如果大于max_count，更新max_count，清空结果，将当前节点的值加入结果中

实现

点击查看代码

class Solution {
public:
    vector<int> findMode(TreeNode* root) {
        result.clear();
        traversal(root);
        return result;
    }
    int max_count = 0;
    TreeNode* pre = nullptr;
    int count = 0;
    vector<int> result;
    void traversal(TreeNode* root){
        if(root == nullptr) return;
        traversal(root->left);
        if(pre == nullptr){
            count = 1;
        }
        else if(pre->val == root->val){
            count++;
        }
        else if(pre->val != root->val){
            count = 1;
        }
        pre = root;
        if(count == max_count){
            result.push_back(root->val);
        }
        else if(count > max_count){
            result.clear();
            max_count = count;
            result.push_back(root->val);
        }
        traversal(root->right);
    }
};

复杂度分析

• 时间复杂度：O(n)
• 空间复杂度：O(n)

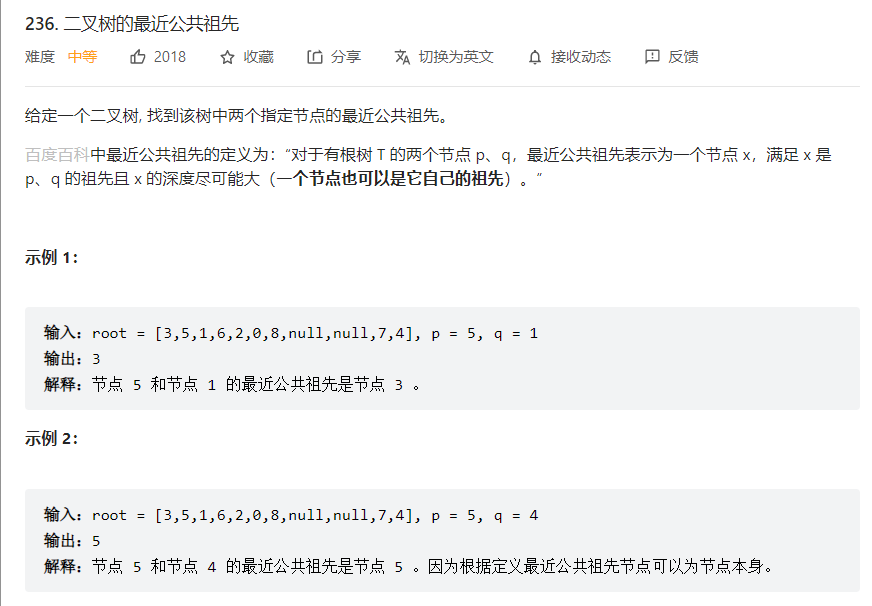
236. 二叉树的最近公共祖先

题目|文章

思路

因为要先处理子节点，因此使用后序遍历是正确的遍历顺序。

1. 确定参数和返回值

2. 确定终止条件。当遍历到节点为空或者节点为p或q时，返回当前节点。

3. 确定单层循环逻辑。对于左子树和右子树返回值的不同情况进行处理。

• 当左右子树都不是空时，当前节点就是最小公共祖先，返回当前节点。
• 当左子树为空时，返回右子树，当右子树为空时，返回左子树
• 当左右子树都为空时，返回空节点。

实现

点击查看代码

class Solution {
public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(root == NULL) return root;
        if(root == p || root == q) return root;
        TreeNode* left = lowestCommonAncestor(root->left, p, q);
        TreeNode* right = lowestCommonAncestor(root->right,p , q);
        if(left != NULL && right != NULL) return root;
        else if(left == NULL && right != NULL) return right;
        else if(left != NULL && right == NULL) return left;
        else return NULL;   
    }
};

复杂度分析

• 时间复杂度：O(n)
• 空间复杂度：O(n)