代码随想录day16 | 104. 二叉树的最大深度 111. 二叉树的最小深度 222. 完全二叉树的节点个数

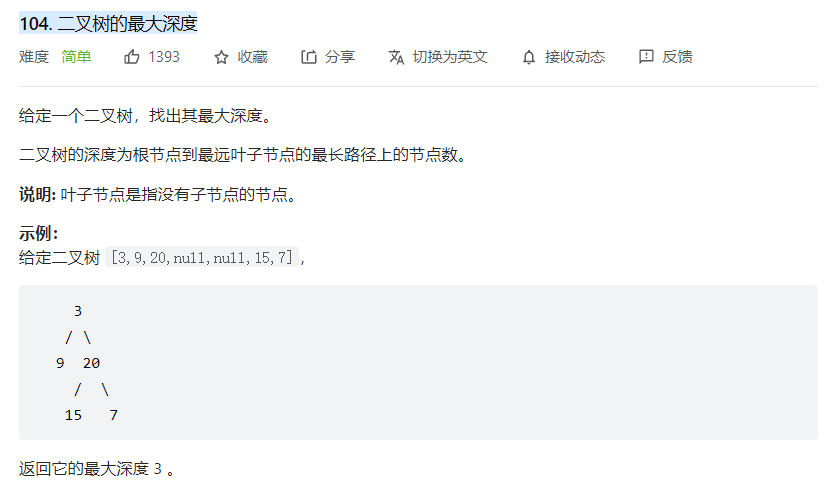
104. 二叉树的最大深度

题目|文章

1.前序遍历+递归(求深度)

思路

通过不断传递深度depth来实现回溯。

实现

点击查看代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        if(root == nullptr)return 0;
        getDepth(root,1);
        return result;
    }
    int result;
    void getDepth(TreeNode* cur,int depth){
        result = result > depth ? result :depth;
        if(cur->left)getDepth(cur->left,depth+1);
        if(cur->right)getDepth(cur->right,depth+1); 
    }
};

复杂度分析

• 时间复杂度：O(n)
• 空间复杂度：O(height)

2.后序遍历+递归（求高度）

思路

不断比较左右子节点的高度，求出最大高度。

实现

点击查看代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        return getDepth(root,depth);
    }
    int depth = 1;
    int getDepth(TreeNode* cur,int depth){
        if(cur == nullptr)return 0;
        int leftTree = getDepth(cur->left,depth);
        int rightTree = getDepth(cur->right,depth);
        depth = 1 + max(leftTree,rightTree);
        return depth;
    }
};

复杂度分析

• 时间复杂度：O(n)
• 空间复杂度：O(height)

3.层序遍历

思路

遍历所有节点，求出最大深度

实现

点击查看代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int maxDepth(TreeNode* root) {
        queue<TreeNode*> que;
        int result = 0;
        if(root == nullptr) return 0;
        que.push(root);
        while(!que.empty()){
            int size = que.size();
            for(int i = 0; i < size; i++){
                TreeNode* cur = que.front();
                que.pop();
                if(cur->left)que.push(cur->left);
                if(cur->right)que.push(cur->right);
            }
            result++;
        } 
        return result;
    }
};

复杂度分析

• 时间复杂度：O(n)
• 空间复杂度：O(n)

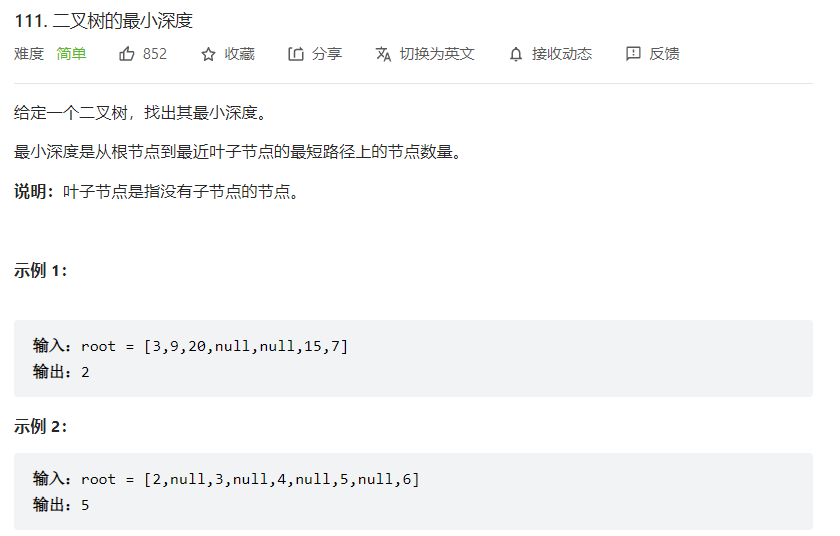
111. 二叉树的最小深度

题目|文章

1.前序遍历+递归

思路

主要对于只有一个子节点的节点的处理。

实现

点击查看代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        if(root == nullptr)return 0;
        getDepth(root,1);
        return result;
    }
    int result = INT32_MAX;
    void getDepth(TreeNode* cur, int depth){
        if(cur->left == nullptr && cur->right == nullptr){
            result = result < depth ? result : depth; 
        }

        if(cur->left)getDepth(cur->left,depth+1);
        if(cur->right)getDepth(cur->right,depth+1);
    }
};

复杂度分析

• 时间复杂度：O(n)
• 空间复杂度：O(H)

2.后序遍历+递归

思路

对于每一个非叶子节点，我们只需要分别计算其左右子树的最小叶子节点深度。这样就将一个大问题转化为了小问题，可以递归地解决该问题

实现

点击查看代码

class Solution {
public:
    int minDepth(TreeNode* root) {
        return getDepth(root,0);
    }
    int getDepth(TreeNode* cur,int depth){
        if(cur == nullptr)return depth;
        int left = getDepth(cur->left,depth);
        int right = getDepth(cur->right,depth);
        if(cur->left == nullptr && cur->right != nullptr)depth = 1 + right;
        else if(cur->left != nullptr && cur->right == nullptr)depth = 1 + left ;
        else depth = 1+min(left,right);
        return depth;
    }
};

复杂度分析

• 时间复杂度：O(n)
• 空间复杂度：O(H)

3.层序遍历

思路

当我们找到一个叶子节点时，直接返回这个叶子节点的深度。广度优先搜索的性质保证了最先搜索到的叶子节点的深度一定最小。

实现

点击查看代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    int minDepth(TreeNode* root) {
        queue<TreeNode*> que;
        int result =0;
        if(root == nullptr)return 0;
        que.push(root);
        while(!que.empty()){
            int size = que.size();
            for(int i = 0; i < size; i++){
                TreeNode* cur = que.front();
                que.pop();
                if(cur->left == nullptr && cur->right == nullptr) return result+1;
                if(cur->left)que.push(cur->left);
                if(cur->right)que.push(cur->right);
            }
            result++;
        }
        return result;

    }
};

复杂度分析

• 时间复杂度：O(n)
• 空间复杂度：O(n)

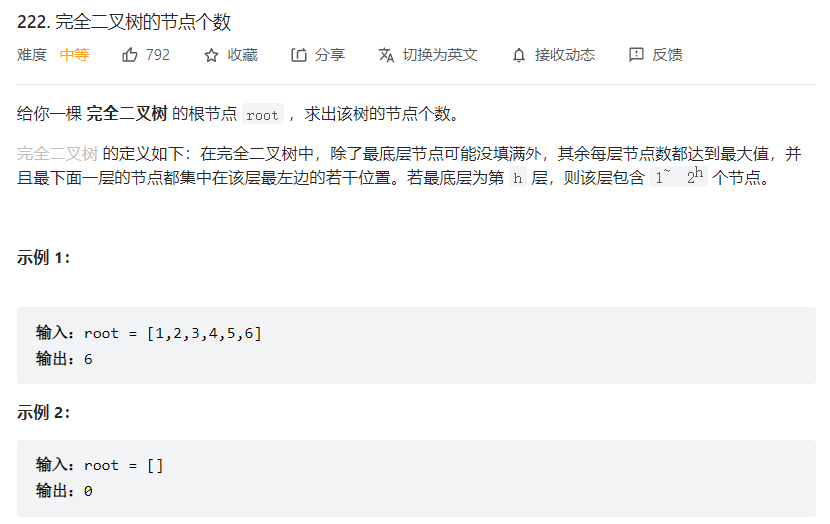
222. 完全二叉树的节点个数

题目|文章

1.完全二叉树特点解法

思路

1.本题的关键在于如果能判断一个子树是满二叉树，那么便可以直接判断出子树的节点个数，从而减少时间复杂度。
2.本题已知是完全二叉树，那么只需遍历判断每个节点是不是满二叉树即可。

实现

点击查看代码

class Solution {
public:
    int countNodes(TreeNode* root) {
        if(root == nullptr)return 0;
        TreeNode* leftNode = root->left;
        TreeNode* rightNode = root->right;
        int left = 0, right = 0;
        while(leftNode){
            left++;
            leftNode = leftNode->left;
        }    
        while(rightNode){
            right++;
            rightNode = rightNode->right;
        }
        if(left == right){
            return (2 << left) - 1;
        }
        left = countNodes(root->left);
        right = countNodes(root->right);
        return left+right+1; 
    }

};

复杂度分析

• 时间复杂度：O(logn*logn)，二叉树的总层数为logn，每一层需要判断logn次。
• 空间复杂度：O(logn)