树和二叉树以及图知识点总结

树和二叉树
树：若干个结点组成的有限集合。
二叉树：每个结点最多拥有两棵子树的树。
满二叉树：在一颗二叉树中，所有分支结点都有左子树和右子树，并且所有叶子结点都在同一层上。
完全二叉树：叶子结点只能出现在最下层和次下层且最下层的叶子结点集中在树的左边。
二叉树的性质
性质1: 在二叉树的第i层上至多有2i-1个结点。
性质2: 深度为k的二叉树至多有2k-1个结点。
性质3: 对于任何一棵二叉树，若2度的结点数有n个，则叶子结点数必定为n＋1  
性质4: 具有n个结点的完全二叉树的深度必为(log2n)+1           
性质5: 对完全二叉树，若从上至下、从左至右编号，则编号为i 的结点，其左孩子编号必为2i，其右孩子编号为2i＋1；其双亲的编号必为i/2（i!＝1）。
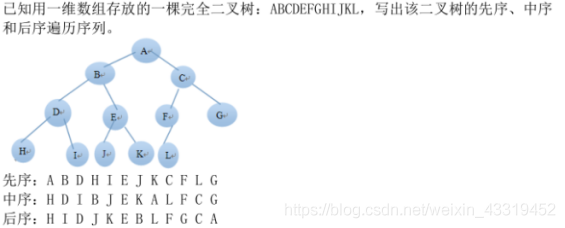
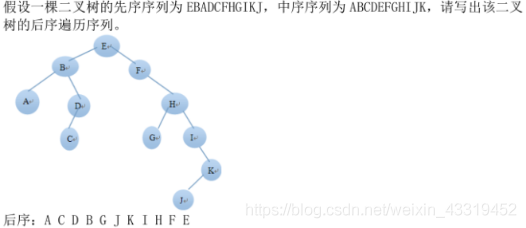
二叉树的遍历:一棵二叉树由根节点、根结点的左子树和根结点的右子树三部分组成。因此只要依次遍历这三个部分，就可以遍历整个二叉树。
DLR(先序遍历)
LDR(中序遍历)
LRD(后序遍历)

 

 

 

 

图
图：由顶点集合及顶点之间的关系集合组成的一种数据结构。  
记为G=(V,E),其中V是G的顶点集合，是有穷非空集；E是G的边集合，是有穷集。
有向图：<x,y>表示从顶点x发向顶点y的边。
路径：两个顶点之间的顶点序列。路径上边的数目为长度。
简单路径：顶点序列中顶点不重复出现的路径。
连通图：图中任意两个顶点都是连通的。

无向图的顶点个数为n，则此图最多包含有n(n-1)/2条边。
有向图的顶点个数为n，若要使任意两点间可以互相到达，则至少需要n条边。
n个顶点的连通图的生成树含有n-1条边。
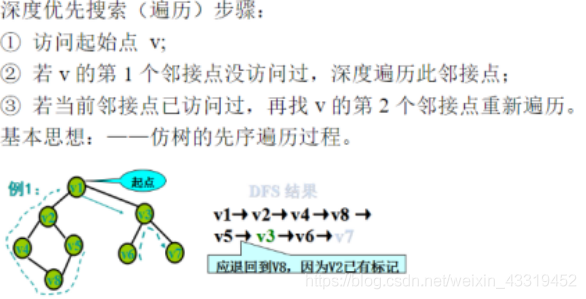
图的遍历：
深度优先搜索

 

 

广度优先搜索

 

 

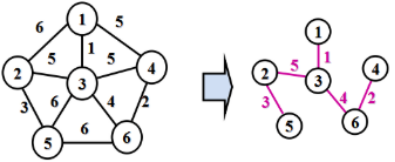
最小生成树：所有生成树中边的权值总和最小的生成树。

Prime(普里姆)算法特点: 集合到集合的最小权值，适于稠密网。

 

 

 

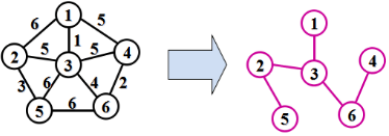
Kruskal(克鲁斯卡尔)算法特点：最小权值之和且不能成环，适于求稀疏网的最小生成树。

 

 

 

————————————————
图的图片链接https://blog.csdn.net/weixin_43319452/article/details/109644369