认识数据结构以及对链表的学习

第一章对认识数据结构

1：问题建模

2: 构造求解算法

3：选择或设计存储结构（空间和时间的性能选）

4：编程实现

5：测试（找bug）

 

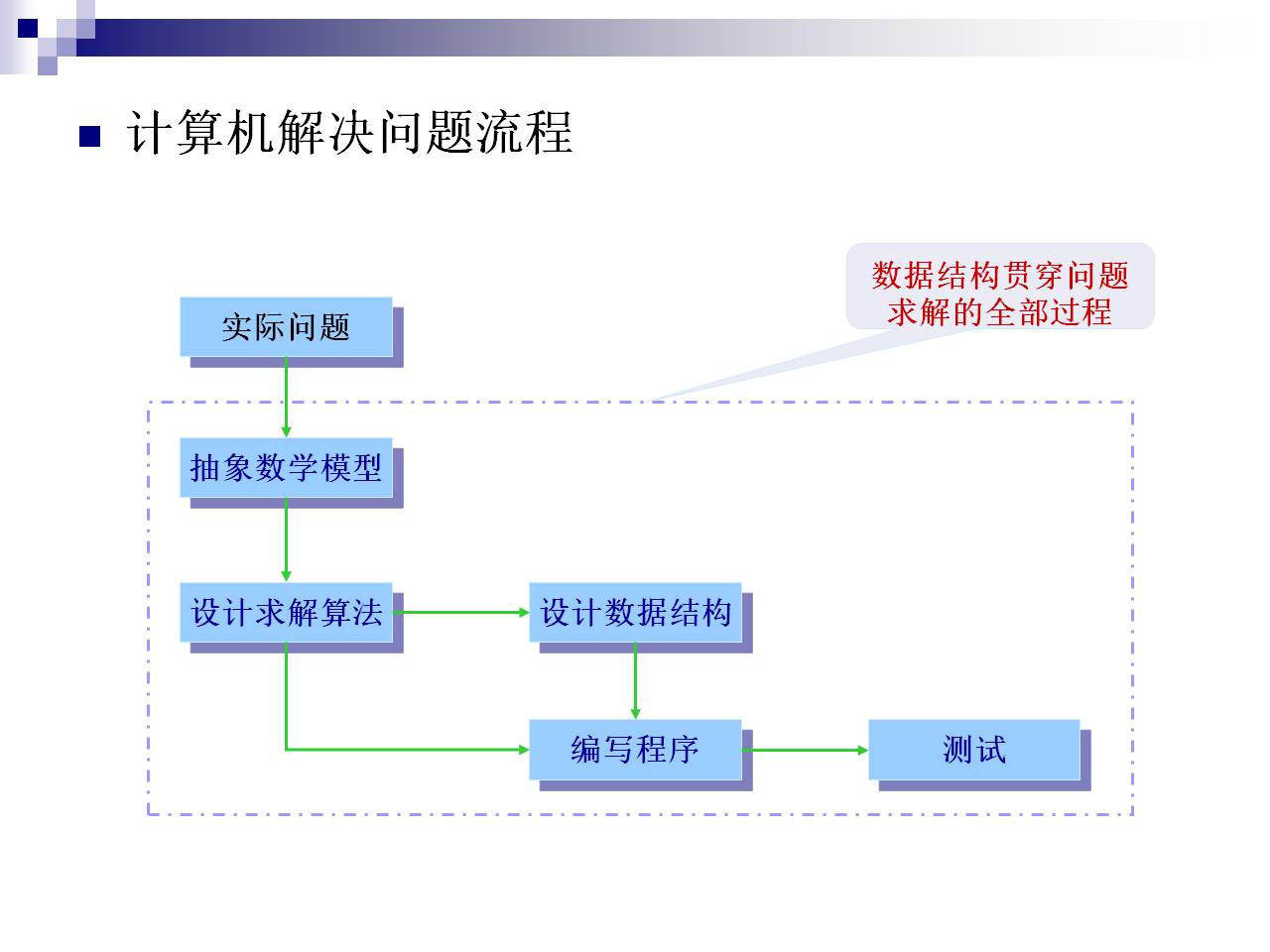
 1.2节：基本概念和术语

1：数据（data）

　　是能够输入到计算机中，并能被计算机处理的符号集合 ，在数据结构中一般是具有一定逻辑结构的数据

2：dataElement（数据元素）：

　　描述数据对象，构成数据的基本单位（具有独立的意义） ； 数据结构中考察数据之间的逻辑关系和运算都是以数据元素（dataElement)为基本单位的

3：数据项（dataItem）:

　　dateElement各种属性的描述信息，是数据中不可分割的最小单元

4：数据结构（dataStructure）

　　构成数据的数据元素（dataElement）之间的结构关系

　　数据结构可以分为三类：逻辑结构

　　　　(1)逻辑结构：按dataElement的逻辑关系分类。集合（元素之间没有关系不能重复），线性结构（元素一对一），树形结构（一对多），图结构（多对多）。

　　　　(2)物理结构：顺序结构（地址连在一起）和链式结构 索引结构 散列结构2022-03-25

　　　（3）运算： 施加在数据结构上的一组操作总称也称为算法

1.3算法

1.3.1算法

　　算法是由若干条指令组成的有穷序列

　　算法的五大特性：输入，输出，有穷性，确定性，可行性。

　　用伪语言（类语言 ）描述{

　　　　引用的使用：它就相当于是java中的实体的管理者，&a = b中的&a是指向&b的内存地址，管理着里面的数据，可以对其进行操作。引用的使用，避免了函数里面二级指针的出现。
　　}

1.4：算法的分析：

　　1，时间复杂度：

　　　　以算法运行中语句的执行次数的数量级来代替

　　　　　　例题：for（i=0； i<n;i++) n = i + 1; 它的复杂度是O（n）

第二章线性表
线性表(List)：n个元素的有限序列
线性表的第i个数据元素ai的存储位置为：
LOC(ai)=LOC(a1)+(i-1)L

顺序表中逻辑上相邻的元素，其物理位置一定相邻。在单链表中，逻辑上相邻的元素，其物理位置不一定相邻。
顺序表中等概率下插入或删除一个元素的时间复杂度为O(n)，修改操作的时间效率是O(1)。
单链表中查找/删除第i个结点的算法时间复杂度为O(n)。
线性表的两种存储结构各自的优缺点：
顺序存储
优点：存储密度大，存储空间利用率高，可随机存取。
缺点：插入或删除元素时不方便。
链式存储
优点：插入或删除元素时很方便，使用灵活；结点空间可以动态申请和释放。
缺点：存储密度小，存储空间利用率低，非随机存取。
若线性表的长度变化不大，且其主要操作是查找，则采用顺序表。
若线性表的长度变化较大，且其主要操作是插入、删除操作，则采用链表。
顺序表(sequenceList)：用一组地址连续的存储单元依次存放线性表的数据元素。

插入–在线性表的第i个位置前插入一个元素
实现步骤:
①将第n至第i位的元素向后移动一个位置;
②将要插入的元素写到第i个位置;
③表长加1。
注意:事先应判断:插入位置i是否合法?表是否已满?
应当符合条件: pos=[1, len+1]
核心语句:
for (i=len; i>=pos; i–){
listArray[i]=listArray[i-1];
}
listArray[pos-1]=obj
链表(linkList)：用一组任意的存储单元来存放线性表的数据元素。

结点的定义

class Node{
T data;
Node next;
Node(Node n){
Next=n;
}
Node(T obj,Node n){
data=obj;
next=n;
}
T getData(){
return data;
}
Node getNext(){
return next;
}
}

 

单链表的查找(带头结点)

Int num=1;
Node p=head,q=head.next;
while(num<pos){
    p=q;
    q=q.next;
    num++;
}

 

单链表的插入结点s
Step 1：s->next=p->next;
Step 2：p->next=s;

单链表的删除
T x=q.data;
p.next=q.next;

头结点的判空条件：
不带头结点：head == null;
带头结点：head.next == null;

栈和队列
栈(stack)：仅在表尾(栈顶)进行插入和删除操作的线性表。
顺序栈(sequenceStack)：利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素，定义top指向栈顶元素。

入栈
top++;
stackArray[top]=obj;

出栈
T x=stackArray[top];
top–;

链栈(不带空的头结点）
向一个栈顶指针为HS的链栈中插入一个s所指结点
s next= HS;
HS=s;

从一个栈顶指针为HS的链栈中删除一个结点
x=HS data;
HS= HS. next;

一个栈的入栈序列a，b，c，d，e，则栈的不可能的输出序列是 C
A edcba B. decba C. dceab D abcde
什么叫“假溢出” ？如何解决？ 
在顺序队列中，当尾指针已经到了数组的上界，不能再有入队操作，但其实数组中还有空位置，这就叫“假溢出”。解决假溢出的途径———采用循环队列

队列：队尾插入，队头删除的线性表。
顺序队列：用一组地址连续的存储单元依次存放从队头到队尾的元素，定义front和rear分别指示队列的队头元素和队尾元素。

入队
rear=(rear+1)%queueArray.length;
queueArray[rear]=obj;

出队
front=(front+1)%queueArray.length;
return queueArray[front];

判空
rear == front

判满
(rear+1)%queueArray.length == front