返回一个首尾相连整数数组中最大子数组的和。

一、题目：返回一个整数数组中最大子数组的和。

二、要求：

（1）输入一个整形数组，数组里有正数也有负数。
（2）数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。
（3）如果数组A[0]……A[j-1]首尾相邻，允许A[i-1]， …… A[n-1]， A[0]……A[j-1]之和最大。
（4）同时返回最大子数组的位置。
（5）求所有子数组的和的最大值。

三，设计思路：

           上课思考认为如果不是循环数组的话，是上次练习的一个普通的数组，求他们的连续的最大子数组的和的最大值，例如：1,2,3,4,5 如果是一个普通数组，那组成的数组最大就不是3,4,5，而循环数组是3,4,5,1,2，循环数组从那个数开始，那么相当于在那个数的位置切开，他的最大子数组，就是和他相邻的但是断开后不相邻的那个位置，当截断后可以看成是一个普通数组4,5,1,2,3，那么问题就转换为了第一次普通一维数组的问题。
           那么想求这个数组，我们可以把这个数组扩展一下，如1.2.3.4.5.6.7我们可以扩展成1.2.3.4.5.6.7.1.2.3.4.5.6，也就是在最后一个数的后面再加上他前面的数，然后我们在取最长的子数组的时候，可以按照第二个新构建的数组，从其中取连续的五个，这样就对问题进行了降维。
四，项目代码：

#include<iostream>
#include<time.h>
#define n 20
using namespace std;
void main()
{
    int a[n],i,j,w=0,b[n][n],p1=0,p2=0,t,m;
    srand((int)time(0));
    for(i=0;i<n;i++)
    {
        a[i]=-rand()%36+25;
    }
    for(i=0;i<n;i++)
    {
        cout<<a[i]<<endl;
    }
    for(i=0;i<n;i++)
    {
        m=i;
        w=0;
        j=0;
        while(j<=n-1)
        {
            w+=a[m];
            b[i][j]=w;
            m++;
            if(m>n-1)
            {
                m=0;
            }
            j++;
        }
    }
    t=b[0][0];
    for(i=0;i<n;i++)
    {
        for(j=0;j<n;j++)
        {
            if(b[i][j]>t)
            {
                t=b[i][j];
                p1=i;
                p2=j;
            }
        }
    }
    cout<<"最大子数组的值为："<<t<<endl;
    cout<<"最大子数组中元素的位置为："<<endl;
    i=0;
    while(i<=p2)
    {
        cout<<p1<<"  ";
        p1++;
        if(p1>=n)
        {
            p1=0;
        }
        i++;
    }
        cout<<endl;
}

五：结果截图：

 

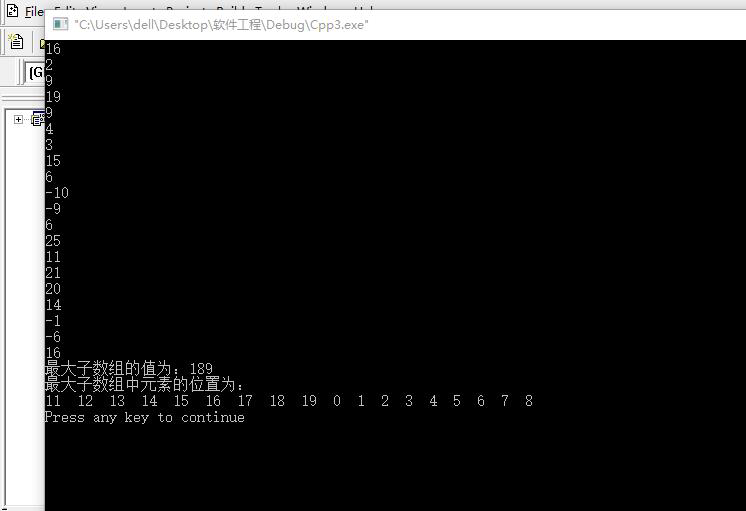
团队照片：