ML-矩阵的运算及其运算规则
一、矩阵的加法与减法1、运算规则 设矩阵 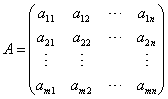 , ,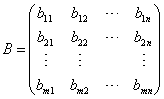 , ,则  简言之,两个矩阵相加减,即它们相同位置的元素相加减! 注意:只有对于两个行数、列数分别相等的矩阵(即同型矩阵),加减法运算才有意义,即加减运算是可行的. |
2、 运算性质 (假设运算都是可行的) 满足交换律和结合律 交换律 结合律 |
二、矩阵与数的乘法1、 运算规则 数 特别地,称 2、 运算性质 满足结合律和分配律 结合律: (λμ)A=λ(μA) ; (λ+μ)A =λA+μA. 分配律: λ (A+B)=λA+λB. |
典型例题 例6.5.1 已知两个矩阵 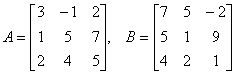 解 由已知条件知 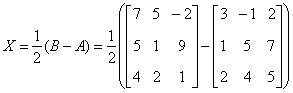  |
三、矩阵与矩阵的乘法1、 运算规则 设 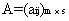 , ,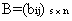 ,则A与B的乘积 ,则A与B的乘积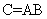 是这样一个矩阵: 是这样一个矩阵:(1) 行数与(左矩阵)A相同,列数与(右矩阵)B相同,即 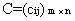 . .(2) C的第  由A的第 由A的第 |
典型例题 例6.5.2 设矩阵 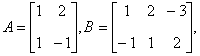 解  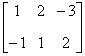 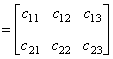  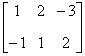 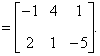 想一想:设列矩阵 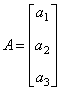 ,行矩阵 ,行矩阵 |
课堂练习 1、设 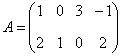 , , ,求 ,求2、在第1道练习题中,两个矩阵相乘的顺序是A在左边,B在右边,称为A左乘B或B右乘A.如果交换顺序,让B在左边,A在右边,即A右乘B,运算还能进行吗?请算算试试看.并由此思考:两个矩阵应当满足什么条件,才能够做乘法运算. 3、设列矩阵 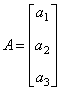 ,行矩阵 ,行矩阵4、设三阶方阵 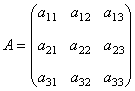 ,三阶单位阵为 ,三阶单位阵为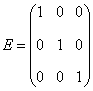 ,试求 ,试求 |
解: 第1题  . .对于 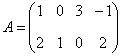 , , . . |
结论1 只有在下列情况下,两个矩阵的乘法才有意义,或说乘法运算是可行的:左矩阵的列数=右矩阵的行数. 第3题 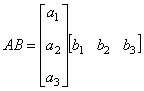 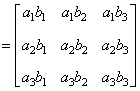 . .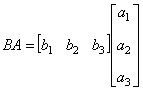 结论2 在矩阵的乘法中,必须注意相乘的顺序.即使在 第4题 计算得: 结论3 方阵A和它同阶的单位阵作乘积,结果仍为A,即 单位阵在矩阵乘法中的作用相当于数1在我们普通乘法中的作用. |
典型例题 例6.5.3 设 解  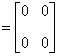 . .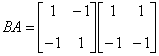  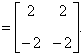 结论4 两个非零矩阵的乘积可以是零矩阵.由此若 |
例6.5.4 利用矩阵的乘法,三元线性方程组 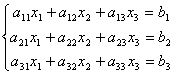 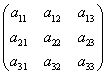 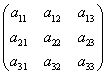 , ,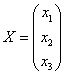 , ,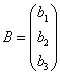 , , |
2、 运算性质(假设运算都是可行的) (1) 结合律 (2) 分配律 (3) 3、 方阵的幂
|
四、矩阵的转置1、 定义
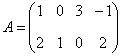 的转置矩阵为 的转置矩阵为 . .2、运算性质(假设运算都是可行的) (1) (2) (3) (4) |
典型例题 例6.5.5 利用矩阵  解 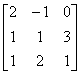 而 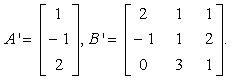 所以 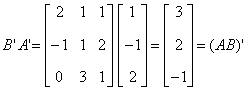 . . |
|
五、方阵的行列式1、定义
2 、运算性质 (1) (2) (3) 思考:设A为 |
不妨自行设计一个二阶方阵,计算一下 例如 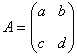 ,则 ,则 . .于是 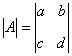 ,而 ,而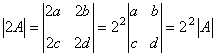 思考:设 解 方法一:先求矩阵乘法 方法二:先分别求行列式 |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号