网络流 题目推荐

提示：想看题目推荐往后翻

前言

网络流在算法竞赛中很常用，也是较为重要的算法，本篇为了使讲解更加通俗易懂，舍去了一些严谨性，恳请谅解。

什么是网络流

准确的说，网络流是一个带权的有向图，标准写法是 \(G = (V, E)\)，该网络上所有点分别编号为 \(1 \sim n\)，所有边分别编号为 \(1\sim m\)，其中该网络的源点为 \(s\)，汇点为 \(t\)，网络上的每条边 \((u,v)\) 都有一个流量限制 \(w(u,v)\)。

通俗来讲，我们可以理解为这是许多水管组成的下水道，整个被称为 网络，有一个点称为 源点，所有水都从这里流出，汇点可以流出无限多的水，汇点连向许多管道，每个管道有流量限制（管道粗细），最终经过一些管道，一定量的水会汇聚到一个点——汇点。

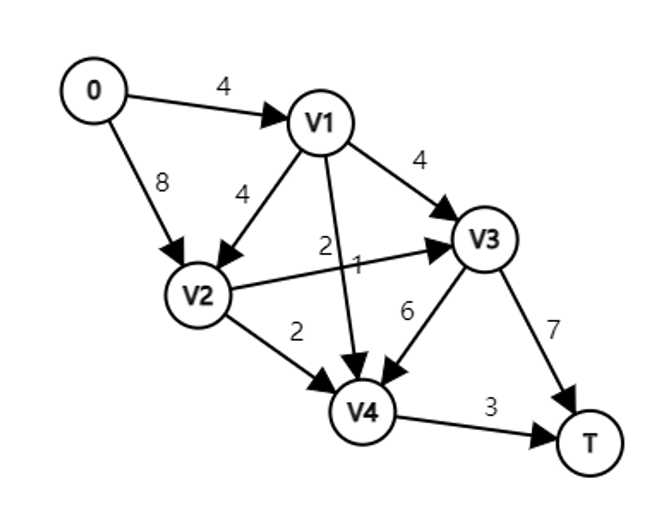
如图就是一个合法的网络。

接下来有几个概念：

• 可行流：如上图，\(0 → V1 → V3 → T\) 就是一个可行流，流向 T 的流量为 4，因为路径上对流量的最小限制为 4。

• 增广路：也称可改进路，指走完这条路径后，每条边扣除走过的流量，留下的图成为 残余网络，再在残余网络上重新找到新的路径，这就是一条增广路。

Ford-Fulkerson 算法

Ford-Fulkerson，简称FF, FF是一种简单的网络流算法，就是每次 dfs 在残余网络寻找新的增广路，不断更新最大流量，但这个算法速度较慢（但很好理解），我们直接学习 更快 的 Dinic 算法。

Dinic 算法

Dinic 相比 FF 要更快

• 使用多路增广，即类似用 dfs 写出类似 bfs 的感觉，u 通过一条边，流出了流量，v 获得流量后，直到这条路走完，再返回 v 流出的流量，如果 u 还有余流，则把余流分配给 u 流出的其他边。

• 用 bfs 对图进行分层，每个点有一个层级，每次流向下一层的点，如果无法流出，则把这个点往上提一层。

• 注意我们要建反向边，用于当前路径不够优时，有一次反悔的机会，记得反向边流量设为 0，保证反悔的时候没有损失流量。

• 当前弧优化： 在 dfs 时，流量留到第 i 条弧时，那前 i - 1 条弧一定被流满了，那下次再访问这个节点时，我们就直接从第 i 条弧开始枚举，这是一个小小的优化。

接下来给出代码，可以去提交模板题：P3376 【模板】网络最大流

#include <bits/stdc++.h>
#define ll long long
using namespace std;
const int MAXN = 200005;
const ll INF = 1e18;
template<typename T>
inline T read() {  
    T X = 0, w = 0; char ch = 0;
    while (!isdigit(ch)) { w |= ch == '-'; ch = getchar(); }
    while (isdigit(ch)) X = (X << 3) + (X << 1) + (ch ^ 48), ch = getchar();
    return w ? -X : X;
}
int n, m, s, t, cnt = 1;
ll ans, d[MAXN];
int now[MAXN];
struct e{
	int t; 
	long long w; 
	int next;
}edge[MAXN];
int head[MAXN];
inline bool bfs() {
	memset(d, 0, sizeof(d));
	d[s] = 1;
	queue<int> q;
	q.push(s);
	now[s] = head[s];
	while(!q.empty()) {
		int x = q.front();
		q.pop();
		for(int i = now[x]; i; i = edge[i].next) {
			if(d[edge[i].t] == 0 && edge[i].w != 0) {
				now[edge[i].t] = head[edge[i].t];
				d[edge[i].t] = d[x] + 1;
				q.push(edge[i].t);
			}
		}
	}
	return d[t];
}
inline ll dfs(int x, ll flow) {
	if(x == t) return flow;
	ll sum = 0;
	for(int i = now[x]; i; i = edge[i].next) {
		now[x] = i;
		if(edge[i].w != 0 && d[edge[i].t] == d[x] + 1) {
			ll tmp = dfs(edge[i].t, min(flow - sum, edge[i].w));
			edge[i].w -= tmp;
			edge[i ^ 1].w += tmp;
			sum += tmp;
			if(sum == flow) return sum;
		}
	}
	return sum;
}
inline void add(int u, int v, ll w) {
	edge[++cnt].next = head[u];
	edge[cnt].w = w; 
	edge[cnt].t = v;
	head[u] = cnt;
}
int main() {
    n = read<int>(), m = read<int>(), s = read<int>(), t = read<int>();
	for(int i = 1; i <= m; i++) {
		int u, v; ll w;
		u = read<int>(), v = read<int>(), w = read<int>();
		add(u, v, w);
		add(v, u, 0);
	}
	while(bfs()) {
		ans += dfs(s, 1e18);
	}
	cout << ans << "\n";
	return 0;
} 

题目推荐

具体可以看这个题单，在洛谷上