洛谷P6017 仙人掌（组合数学）

首先研究一下subtask 5怎么搞。

手玩一下不难发现：满足总和为$2m-2$且每个数不小于1的数列都是满足要求的。这就给了我们启发：可不可以直接找出度数序列数量呢？

接下来解决一个问题：$n$个结点的仙人掌最多有几条边？

不难发现，所有包含点数大于4个的环都是不优的，例如5个点的环可以改成6条边的两个环：

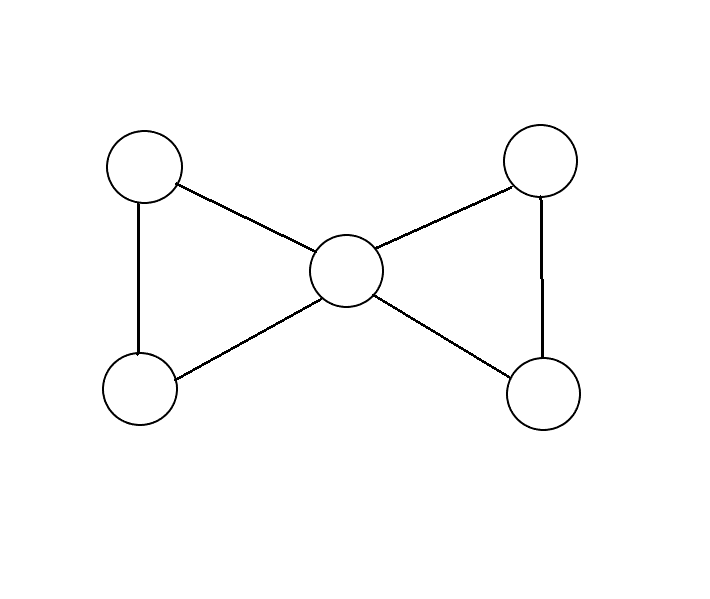
这样就可以得到，$n$为奇数时，$m=\frac{3}{2}(n-1)$：

$n$为偶数时，$m=\frac{3}{2}n-2$：

同时，不难发现，若所有结点的度数均为偶数，这样的仙人掌必定存在（找出度数最大的3个点，连一个环，缩成一个点，一路执行下去就可以了）

对于奇数点，我们发现，把奇数点像下图一样两两配对，就可以转化到偶数的情况：

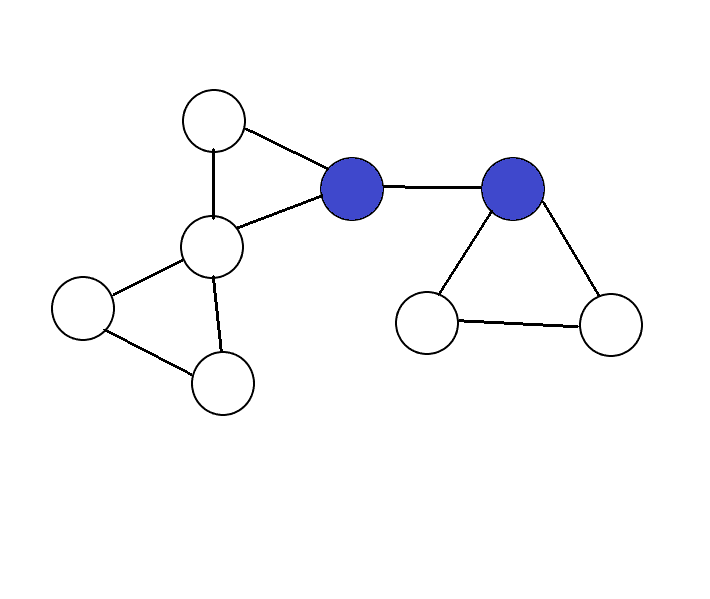
（合并两个蓝点，就转化为第二个图）

不过这样有例外：对于度为1的点，我们不能另找一个度为1的点配对（不然就不连通了），只能找一个度更大的奇数点或把它拼到偶数点上去。

那么，结果只跟$n$，$m$，1点个数$c_1$，奇数点个数$c_{odd}$有关，直接DP是$O(n^4)$的，考虑优化求所有结点的度数均为偶数的序列个数的部分。

把每个点的度除以2，那么就变成了把$m$个无差别的小球放入$n$个无差别的口袋，每个口袋至少有一个球的方案数，依据隔板法，答案为$C^{n-1}_{m-1}$。

对于原问题，我们首先求出$n'=n-c_1,m'=m-\frac{c_1+c_{odd}}{2}$的全为偶数的方案数，然后在$n'$个中找$c_{odd}$个变成奇数（方案数$C^{c_{odd}}_{n'}$），再加上$c_1$个度为1的点（方案数$C^{c_1}_{n}$），这样就可以$O(n^2)$计算啦

#include<cstdio>
#define For(i,A,B) for(i=(A);i<=(B);++i)
typedef long long ll;
const int mod=998244353;
int f[3005],g[3005];
void exgcd(int a,int b,int &x,int &y){
    if(!b){x=1;y=0;}
    else{
        exgcd(b,a%b,y,x);
        y-=a/b*x;
    }
}
inline int inv(int a){
    int x,y;
    exgcd(a,mod,x,y);
    return x<0?x+mod:x;
}
inline int C(int m,int n){return m<=n?(ll)f[n]*g[m]%mod*g[n-m]%mod:0;}
inline int maxm(int n){return n&1?(n-1>>1)*3:(n>>1)*3-2;}
inline bool check(int n,int m,int c1,int co){  //检查转化后是否是合法情况
    if(c1>co){n-=c1;m-=c1;}  //1点太多，只能去和偶数点配对
    else{n-=c1+co>>1;m-=c1+co>>1;}
    return m>=n-1&&m<=maxm(n);
}
int main(){
    int T,n,m,nn,mm,i,j,ans;
    scanf("%d",&T);
    f[0]=f[1]=g[0]=g[1]=1;
    For(i,2,2997)f[i]=(ll)f[i-1]*i%mod;
    g[2997]=inv(f[2997]);
    for(i=2996;i>1;--i)g[i]=(ll)g[i+1]*(i+1)%mod;
    while(T--){
        scanf("%d%d",&n,&m);
        if(m<n-1||m>maxm(n)){
            puts("0");
            continue;
        }
        ans=0;
        For(i,0,n-1)
            For(j,0,n-i)if(i+j*3<=(m<<1))if(!(i+j&1)&&check(n,m,i,j)){
                nn=n-i;mm=m-(i+j>>1);
                ans=(ans+(ll)C(nn-1,mm-1)*C(i,n)%mod*C(j,nn))%mod;
            }else;
            else break;
        printf("%d\n",ans);
    }
    return 0;
}