【数据结构】第六章启航：图论入门——从零掌握有向图、无向图与简单图

导读

大家好，很高兴又和大家见面啦！！！

【数据结构】这门课主要会学习2种结构：

线性结构
非线性结构

而线性结构中的顺序表、链表、栈、队列、串、矩阵、数组我们已经学完了。非线性结构中的树、集合我们也已经学完了。下面我们就将进入【数据结构】的最后一个非线性结构——图的学习。

在第六章——图这个章节中，我们会分为4个板块来学习：

图的基本概念
图的存储与基本操作
图的遍历
图的基本应用

从今天开始，我们会进入图的第一个板块——图的基本概念的学习。我们会在今天的内容中，知道什么是图？图有哪些分类？以及图中的一些重要概念。下面我们就一起进入今天的内容吧！！！

一、图的定义

图（Graph）是数据结构中一种重要的非线性结构，用于表示对象之间的关系。它由顶点（Vertex）和边（Edge）组成，能够建模复杂的关联关系，广泛应用于社交网络、路径规划、推荐系统等领域。

图 $G$ 是由顶点集 $V$ 和边集 $E$ 组成，记为 $G = (V, E)$ ，其中 $V (G)$ 表示图 $G$ 中的顶点的有限非空集； $E (G)$ 表示图 $G$ 中顶点之间的关系（边）集合。

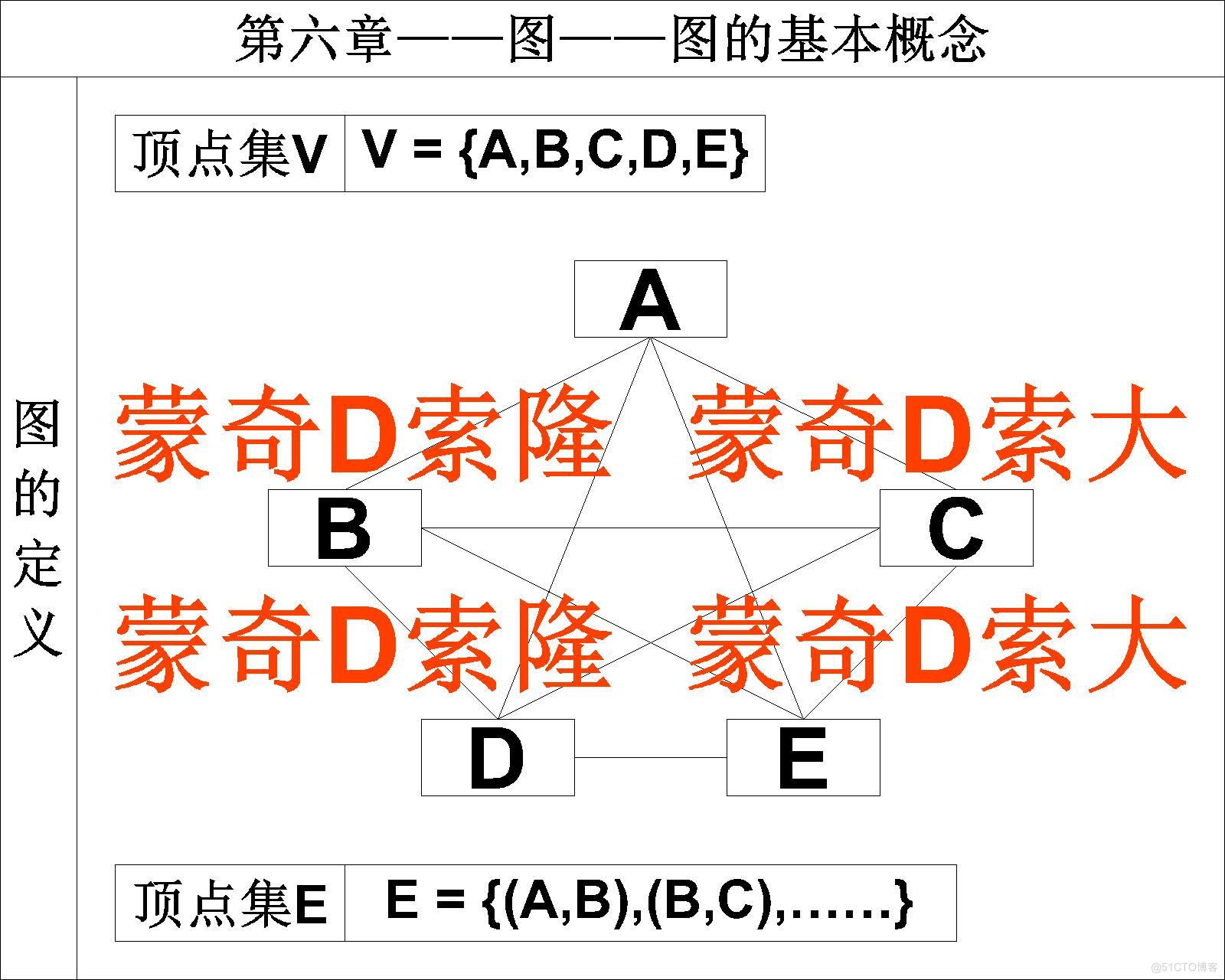
这里我们以上图中展示的图来进一步的认识图中的顶点与边。

所谓的顶点，就是A/B/C/D/E这些结点；边指的就是连接这些顶点的线。在一个图中，可以顶点与顶点之间可以没有线连接，即边集可以为空集；但是不存在没有顶点的图，即顶点集一定是非空集。

举一个最简单的例子，在上图中，如果我们只看结点A，其它都不看，此时的结点A就是一个图：

graph LR
A

再说一个我们比较熟悉的例子，我们目前所学的数据结构：

线性结构：顺序表、链表、栈、队列、串、矩阵
非线性结构：
- 树形结构：树、m叉树、森林
- 集合
- 并查集

这些都可以看做一种特殊图。这是因为这些数据结构都是由顶点与边构成：

线性结构：由n个顶点和n-1条边构成的单链路径的图，无环无分支；

graph LR
a-->b-->c-->d

树形结构：由n个顶点与n-1条边构成的有向无环图

graph TD
a-->b
a-->c

集合：由n个顶点与0条边构成的零图

graph TD
a
b
c

并查集：由多个无向无环图构成

graph TD
a-->b
a-->c
d-->e
d-->f

那也就是说，只要是由顶点与将各个顶点连接起来的边就能得到图；

在图 $G$ 中，若 $V = v_{1}, v_{2}, v_{3} \dots \dots$ ，则我们可以用 $| V |$ 表示图 $G$ 中顶点的个数，也称为图 $G$ 的阶， $E = (u, v) | u \in V ， v \in V$ ，用 $| E |$ 表示图 $G$ 中边的条数。

在线性表、树中我们都有提到过一种特殊情况——空表、空树。也就是说在线性表和树中可以什么都没有，但是在图中不行，图不存在空图。

接下来我们就来认识一下图中的一些基本概念与术语；

二、图的分类

2.1 有向图与无向图

在图中，我们根据边是否有明确的方向指示将图分为两类：

有向图

若E为有向边（也称弧）的有限集合，则图G为有向图。

弧是顶点的有序对，记为 $< v, w >$

其中v与w是顶点，v称为弧尾，w称为弧头； $< v, w >$

graph LR
a--弧-->b--弧-->c--弧-->a

上图可表示为： $G = (V, E)$ $V = a, b, c$ $E = < a, b >, < b, c >, < c, a >$

在上图中，存在3条弧：

$< a, b >$
$< b, c >$
$< c, a >$

当我们在表述一条弧时，我们采用前两种中的任意一种即可，第3条弧，我是为了给大家展示两种说法都是可行的，没有其它的含义。

无向图

若E是无向边（简称边）的有限集合，则图G称为无向图。

边是顶点的无序对，记为 $(v, w)$ 或 $(w, v)$ 。可以说w与v互为邻接点。

边 $(v, w)$ 依附于w和v，也可以称为边 $(v, w)$ 和v，w相关联。

graph LR
a--边---b
b--边---c
c--边---a

上图可表示为： $G = (V, E)$ $V = a, b, c$ $E = (a, b), (b, c), (c, a)$

在上图中，有3条边：

$(a, b)$ ：边 $(a, b)$ 依附于a和b
$(b, c)$ ：边 $(b, c)$ 与b和c相关联
$(c, a)$ ：边 $(c, a)$ 依附于a和c

在无向图中，由于没有起点与终点之分，因此我们在表述时，不需要在意顶点的先后顺序

2.2 简单图与多重图

按照边是否重复，我们可以将图分为两类：

简单图

一个图G若满足：

不存在重复边
不存在顶点到自身的边

则图G称为简单图。

graph LR
a-->b-->c-->a

像上图这种没有重复边且不存在自环的图就是简单图，前面展示的有向图与无向图都是简单图

多重图

与简单图相反，多重图中会存在三种情况：

仅有重复边（或弧），不允许自环

graph LR
a-->b-->c-->a
a-->b

像上图这种有多条重复的弧，但是没有出现自环的图就是狭义上的多重图；

仅有自环，无重复边（或弧）

graph LR
a-->a-->b-->c-->a

像上图这种存在自环，但是无重复弧的图也属于多重图，但是我们将其称为伪图；

既有重复边，又有自环

graph LR
a-->a-->b-->c-->a
b-->c

像上图这种既存在重复弧，又有自环的图，就是广义上的多重图，也称为伪图。

在本章节的学习中，我们只会学习简单图，不会接触多重图，因此大家只需要对多重图有一个基本的了解即可！！！

三、生活中的图

介绍完了图的两种分类方式，接下来我们就来看一下日常生活中的图：

交通网络

在我们的生活中，交通网络就是一个最直白的有向图的例子，比如我们要从上海去北京，那我们就需要搭乘该方向的交通工具：

graph LR
上海-->北京

上海与北京这就是图中的两个顶点，它们之间的路径就是对应的弧；

人际关系网络

我们在生活中会接触各种各样的人，认识各种各样的朋友，这些交际关系组织成的网络就是一个典型的无向图：

graph LR
小红---小明
小明---小新
小新---小陆
小明---小陆
小新---小红

在人际关系网中，每个人都是一个顶点，人与人之间的联系就是连接两个顶点的边；

思维导图

我们平时不管是在学习，还是工作中，肯定离不开思维导图，这里我们以图这个章节中的思维导图为例：

graph LR
a[图]-->b[基本概念]
a-->c[存储与基本操作]
a-->d[遍历]
a-->e[基本应用]
b-->f[定义]
b-->g[分类]
g-->h[有无方向]
g-->i[有无重复边或自环]

在思维导图中，各知识点就是图中的各个结点，知识点之间的逻辑关系就是连接各个结点的边（或弧）

结语

📌 今日核心要点

1. 图的定义与本质

组成：由顶点集（非空）和边集（可为空）构成，记为 $G = (V, E)$ 。
不可为空：至少含一个顶点，但边可缺失（如单顶点图）。
广义性：线性表、树、集合等均为图的特例（链表是单链路径图，树为有向无环图）。

2. 图的分类

按方向性

有向图：边为有序弧（如 $< a, b >$
无向图：边为无序对（如 $(a, b)$ ），顶点关系对称。

按边复杂度

简单图：禁止重复边与自环，算法研究核心。
多重图：允许重复边/自环，贴近现实场景（如交通多线路）。

3. 现实映射

交通路线（有向）、社交网络（无向）、知识图谱（混合）均为图的实例。

1. 顶点连接性指标

度（Degree）：无向顶点的边数（社交活跃度）。
入度（In-degree）：有向顶点接收的弧数（影响力接收度）。
出度（Out-degree）：有向顶点发出的弧数（信息传播力）。

2. 图的连通性

路径与环路：可达性判断与环路对算法的影响。
连通图与连通分量：如何识别独立子结构（如社交圈层）。

3. 带权图解析

边权重：量化关系的现实意义（如导航距离、通信成本）。

思考题预热：

如何用“出度”识别社交网络中的信息传播枢纽？
若某顶点的入度为0，它在系统中可能扮演什么角色？

原文链接：https://cloud.tencent.com/developer/article/2509283

posted on 2025-11-12 19:40 sunny123456 阅读(0) 评论(0) 收藏举报

刷新页面返回顶部

sunny123456

公告

导读