时间序列分析--长短期记忆模型LSTM

时间序列分析--长短期记忆模型LSTM

PRE

从这一篇开始就进入深度学习领域中的时序模型介绍了，主要集中在RNN架构、Transformer架构以及之前有介绍过的AR-net神经网络，本篇主要介绍LSTM的模型架构及实际python应用，包括在实际建模过程中可以用到的建模技巧。

1、模型原理

长短期记忆（Long short-term memory，简称：LSTM）模型是循环神经网络（RNN）的一个子类型，由 Sepp Hochreiter 和 Jürgen Schmidhuber 在 1997 年开发，近几年已有诸多变体。主要用于识别数据序列，例如传感器数据、股票价格或自然语言中出现的模式。他们的目的是设计一个能够学习存储哪些信息、存​​储多长时间以及丢弃哪些信息的神经网络。这种能力对于处理相关信息跨越较大时间间隔的序列至关重要。

论文原文：

https://www.bioinf.jku.at/publications/older/2604.pdf​www.bioinf.jku.at/publications/older/2604.pdf

LSTM神经网络一大亮点就是其，擅长捕获长期依赖性，使其成为序列预测任务的理想选择。

与传统神经网络不同，LSTM 结合了反馈连接，使其能够处理整个数据序列，而不仅仅是单个数据点。这使得它在理解和预测时序数据（如时间序列、文本和语音）中的模式方面非常有效。

模型架构

首先，简单回顾一下RNN的网络架构，RNN 主要用于检测序列数据中的模式，为了检测数据中的顺序模式，信息通过网络循环传递。这使得 RNN 除了当前输入 X(t) 之外还能够考虑先前输入 X(t-1)。

循环神经网络架构

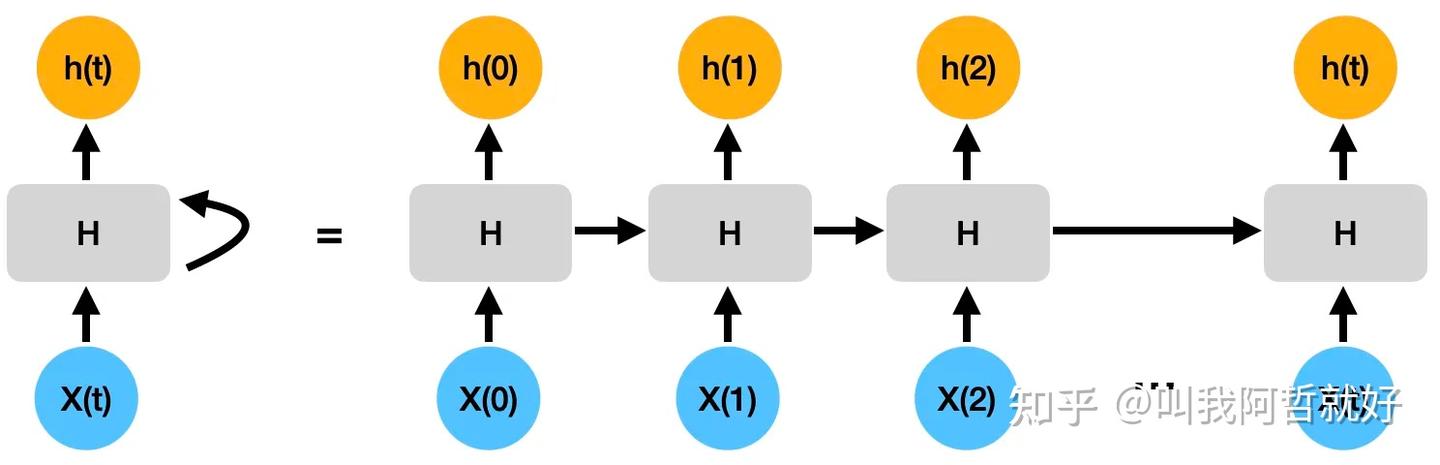
随着序列变得越来越长，当前隐藏状态将需要保留来自先前隐藏状态的信息也变得越来越多，这对于非常长的序列可能会出现梯度消失（或爆炸）。这个时候就需要我们去遗忘一些貌似不那么重要的信息了，那么如何衡量信息是否重要呢？

最简单的逻辑--越久远的信息越不重要，基于自然界自带的先验知识我们能够自然而然的引入这个逻辑。我们工作、生活中，都倾向于参考最近的相似事件从而得出所谓的经验或是参考。如：如何走向成功？明天天气怎么样？

基于这个逻辑。LSTM网络架构就横空出世了。

LSTM 是一种特殊类型的 RNN，其设计目的是比标准 RNN 更好地处理这种长距离依赖性 。当信息通过每个 LSTM 单元时，可以通过门控单元添加或删除信息来更新单元状态 C(t)。

LSTM模型架构

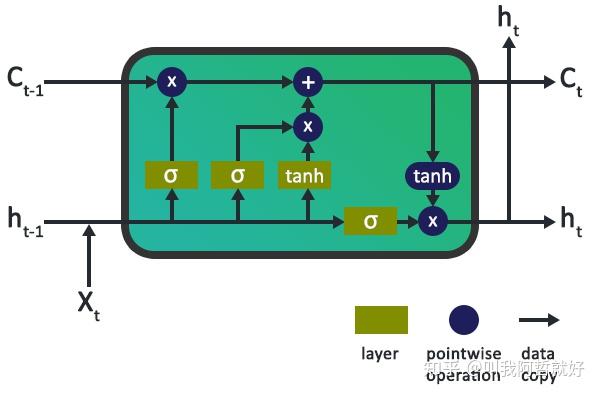
可以看出来，LSTM最大亮点就是为模型引入了所谓的门控单元，那么什么是门控？

门控单元

LSTM 经典架构具有三种门控单元（后续诸多变体会引入其他的门控方式，但多是换汤不换药），三个门控单元主要负责控制进出存储单元或 LSTM 单元的信息流。

第一个门称为遗忘门，第二个门称为输入门，最后一个门称为输出门。

就像简单的 RNN 一样，LSTM 也有一个隐藏状态，其中 H(t-1) 表示前一个时间戳（上一时刻）的隐藏状态，Ht 是当前时刻的隐藏状态。除此之外，LSTM 还分别用 C(t-1) 和 C(t) 分别表示先前和当前时刻的单元状态。

「遗忘门」

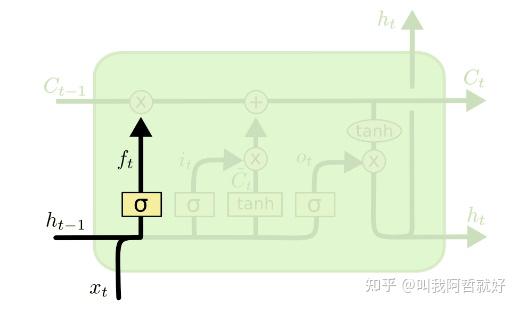
在 LSTM 神经网络的单元中，第一步是决定是否应该保留上一个时间步的信息或忘记它。

Forget Gate：

f_t=\sigma(x_t*U_f+H_{t-1}*W_f) ，

其中

• x_t ：输入当前时间戳。
• U_f ：与输入相关的权重矩阵
• H_{t-1} ：前一个时间戳的隐藏状态
• W_f ：与隐藏状态相关的权重矩阵

随后，对其应用 sigmoid 型的激活函数。这将 f_t 压缩映射 成为 0 到 1 之间的数字。稍后将此f_t与前一个时间戳的单元状态相乘，来判断上一时刻单元所携带的信息，是否应该忘记？应该忘记多少？如下所示：

C_{t-1}*f_t=0 ,,if f_t=0 (forget everything)

C_{t-1}*f_t=C_{t-1} ,,if f_t=1 (forget nothing)

「输入门」

输入门主要用于量化输入所携带的新信息的重要性。

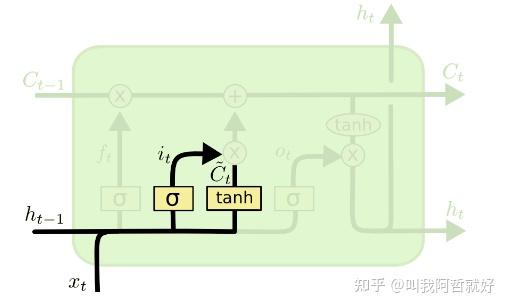
Input Gate：

i_t=\sigma(x_t*U_i+H_{t-1}*W_i)

其中：

• x_t ：当前时间戳t处的输入
• U_i ：输入的权重矩阵
• H_{t-1} ：前一个时间戳的隐藏状态
• W_i ：与隐藏状态相关的权重矩阵

与遗忘门一致，再次对其输出应用了 sigmoid型函数。将其映射为0到1之间。

N_t=tanh(x_t*U_c+H_{t-1}*W_c) (new information)

现在需要传递给单元状态的新信息是前一个时间戳 t-1 处的隐藏状态和时间戳 t 处的输入 x 的函数。

但是，N_t 不会直接添加到细胞状态中,而是利用上述输入门提供的权重，进行衡量重要性，结合遗忘门对历史信息的加权，就得到了我们当前t时刻单元状态的计算公式：

C_t=f_t*C_{t-1}+i_t*N_t

「输出门」

输出门负责决定应该从当前时间步的细胞状态中输出多少信息到当前时间步的隐藏状态。输出门的计算过程涉及当前时间步的输入，前一时间步的隐藏状态以及当前时间步的细胞状态。

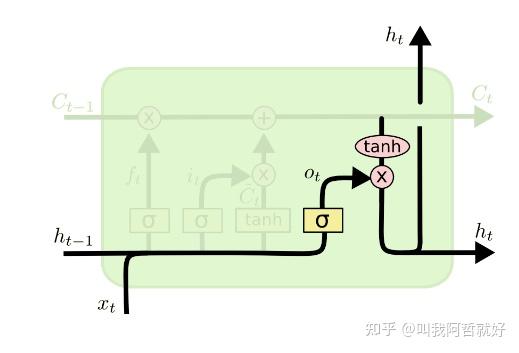
Output Gate：

O_t=\sigma(x_t*U_o+H_{t-1}*W_o)

计算当前时刻的隐藏状态，传到下一时刻：

H_t=O_t*tanh(C_t)

最后通过softmax进行线性映射：

output=Softmax(H_t)

变体

LSTM至今为止已有较多变体，但是核心思想都一致，几乎每一篇涉及 LSTM 的论文都使用略有不同的版本。

Gers 和 Schmidhuber (2000)提出的一种流行的 LSTM 变体是添加“窥视孔连接”。这意味着我们让门层查看单元状态。

还有一种较为流行的变体，是使用耦合的遗忘门和输入门，核心思想为只有当模型忘记旧的东西时，我们才会向状态输入新值。较为出名的就是Cho 等人2014年提出的门控循环单元 (GRU)。通过将遗忘门和输入门组合成一个“更新门”。还合并了单元状态和隐藏状态，并进行了一些其他更改。由此产生的模型比标准 LSTM 模型更简单，并且越来越受欢迎。

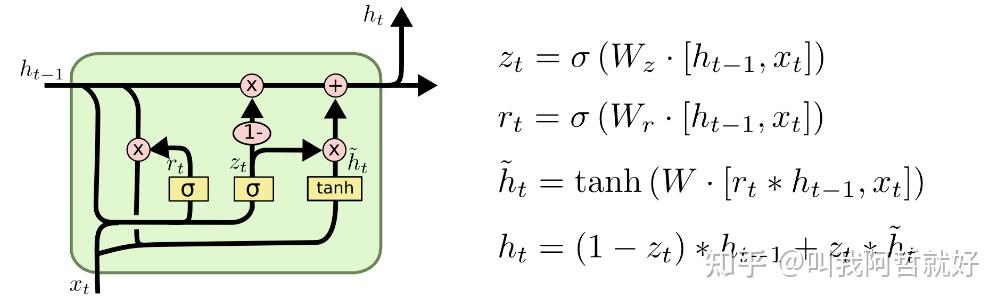
2、建模应用

标准模型框架

选用tensorflow框架下LSTM模块进行建模。

import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
from sklearn.preprocessing import MinMaxScaler
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Dropout
from tensorflow.keras.layers import LSTM
import math
from sklearn.metrics import mean_squared_error
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签

plt.rcParams['axes.unicode_minus'] = False 

关于时间序列数据处理方面就不再过多赘述了，之前有一片文章将方法罗列的挺详尽了，还不清楚的朋友可以移步：时间序列建模问题，如何准确的建立时间序列模型？ - 叫我阿哲就好的回答 - 知乎

设置预估步长，传统LSTM预估核心思想就是自回归模型，根据历史多少天的数据预测下一步的数据情况，称之为单步预测。time_step = 60，表示根据历史60天的数据预估第61天的情况。每过60步进行一次分组，获得X和Y的数据组。

def create_dataset(dataset, time_step = 1):

dataX,dataY = [],[]

for i in range(len(dataset)-time_step-1):

dataX.append(dataset[i:i+time_step])

dataY.append(dataset[i+time_step])

return np.array(dataX),np.array(dataY)

time_step = 60

X_train,Y_train =  create_dataset(train_data,time_step)

X_test,Y_test =  create_dataset(test_data,time_step)

搭建模型框架，模型积木可以自行擂，这里贴出我常用的框架以供参考：

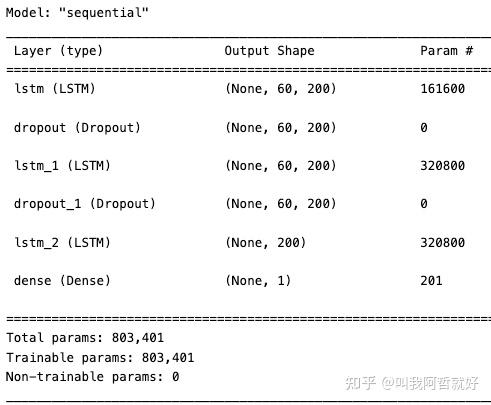
模型包含三个LSTM层和一个全连接层：

1. model = Sequential(): 创建一个Sequential模型，这是Keras中定义神经网络模型的一种简单方法，它是按顺序堆叠层的容器。
2. model.add(LSTM(200, return_sequences=True, input_shape=(X_train.shape[1],1))): 添加一个具有200个神经元的LSTM层到模型中。
3. input_shape=(X_train.shape[1], 1)指定了输入数据的形状，其中X_train.shape[1]表示时间步数。
4. model.add(Dropout(0.2)): 添加一个20%的Dropout层，这有助于防止过拟合。
5. model.add(Dense(1)): 添加一个具有一个神经元的全连接层，用于输出一个值。
6. model.compile(loss='mean_squared_error', optimizer='adam'): 编译模型。使用均方误差（mean squared error）作为损失函数，Adam优化器（优化算法）作为优化器。

model = Sequential()

model.add(LSTM(200,return_sequences = True,input_shape = (X_train.shape[1],1)))

model.add(Dropout(0.2))

model.add(LSTM(200,return_sequences = True))

model.add(Dropout(0.2))

model.add(LSTM(200))

model.add(Dense(1))

model.compile(loss = 'mean_squared_error',optimizer = 'adam')

具体实操可以自行调整参数和框架，model.summary()

模型训练

model.fit(X_train,Y_train,validation_data = (X_test,Y_test),epochs = 80,batch_size = 64,verbose = 1)

效果检验

look_back = 60

trainPredictPlot = np.empty_like(df2)

trainPredictPlot[:,:] = np.nan

trainPredictPlot[look_back : len(train_predict)+look_back,:] = train_predict

plt.plot(scaler.inverse_transform(df2))

plt.plot(trainPredictPlot)

plt.plot(testPredictPlot)

plt.show()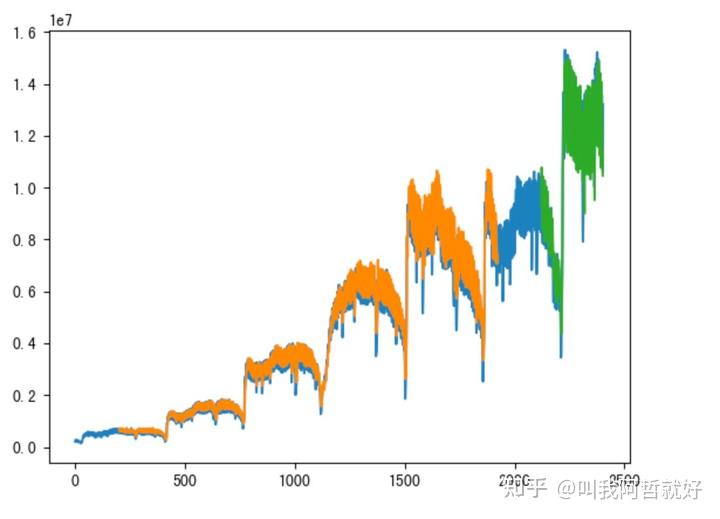

是不是看起来还不错？但是，致命的问题是上述框架为单步预测框架，也就是说每一个预估的值都是基于历史60天的数据进行训练的，这就涉及到了模型使用真实的“未来”数据进行过拟合训练的问题，使用这样的模型进行长时多步的预估任务，就会出现比较大的问题。因为误差在不断叠加。

我们没有办法及时为模型补充真实准确的数据作为训练集，比如我们需要预估未来60天的流量，可能明天的预估还较为准确，但是等到第60天的时候，误差已经无限累加了。即模型是一个滑动窗口，滑到越靠后的位置，预估误差就越大。

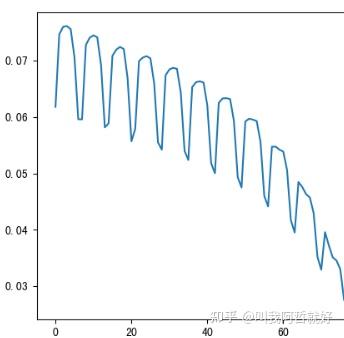
这就是自回归模型，单步预测最为致命的一个缺点，那么能否通过一些小技巧，使得LSTM能够很好的适配长时预估的任务呢？

答案是肯定的。

trick

构建为监督学习问题

# 构建监督学习问题

look_back =90  # 历史时间步数

look_ahead = 60  # 预测的未来时间步数

X, y = [], []

for i in range(len(df2) - look_back - look_ahead + 1):

X.append(df2[i : i + look_back])

y.append(df2[i + look_back : i + look_back + look_ahead])
X, y = np.array(X), np.array(y)
划分训练集和测试集
train_size = int(0.8 * len(X))

X_train, X_test = X[:train_size], X[train_size:]

y_train, y_test = y[:train_size], y[train_size:]
创建 LSTM 模型
model = Sequential()

model.add(LSTM(200,return_sequences = True,input_shape = (X_train.shape[1],1)))

model.add(Dropout(0.2))

model.add(LSTM(200,return_sequences = True))

model.add(Dropout(0.2))

model.add(LSTM(200))

model.add(Dense(look_ahead))

model.compile(optimizer='adam', loss='mse')
模型训练1
model.fit(X_train, y_train, epochs=100, batch_size=64, verbose=1)
预测
y_pred = model.predict(X_test)
反归一化预测结果
y_pred_original = scaler.inverse_transform(y_pred.reshape(-1, 1))

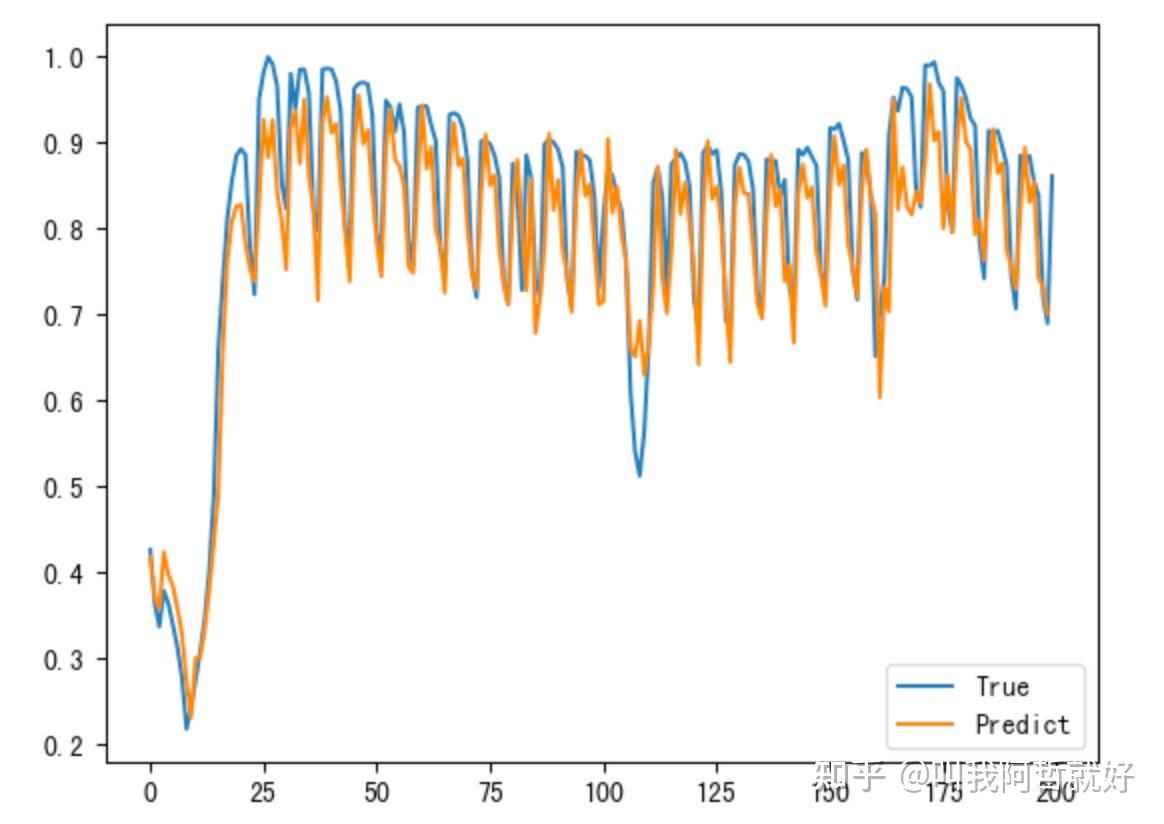
# 绘制预测结果

plt.figure(figsize=(10, 6))

plt.plot(y_test, label="Actual Data")

plt.plot(pred1, label="Predicted Data1")

plt.plot(pred10, label="Predicted Data10")

plt.legend()

plt.title("Multi-Step LSTM Time Series Forecast")

plt.show()

这篇已大致提到了单步预估、多步预估的区别，后续会介绍更多能够好适配长时预估任务的预估模型，核心思想就是要么转化为非自回归训练任务，如之前介绍的Time-GPT，训练了大量的外部时序语料库。

如何为GPT/LLM模型添加额外知识？ - 叫我阿哲就好的回答 - 知乎

要么就是结合能够更好捕捉趋势性的模型，后续继续介绍基于Transformer框架的时序预估模型。

END

针对单一时间序列（无论是单变量还是多变量）定制模型的时代早已一去不复返了。

如今，在大数据时代，创建新数据点的成本极其低廉，时间序列可以是多元的，具有不同的分布，并且可能伴随着额外的探索变量。同时伴随着常见的问题：缺失数据、趋势、季节性、波动性、漂移和罕见事件；为了创建一个具有预测能力的竞争模型，除了历史数据之外，所有变量都应该考虑在内。

最先进的时间序列模型应该考虑哪些规范？

下一篇聊一下

原文链接：https://zhuanlan.zhihu.com/p/681877938