Normalized Mutual Information(NMI, 归一化互信息)

Normalized Mutual Information(NMI, 归一化互信息)

归一化互信息（NMI）是用于衡量两个分类或聚类结果之间相似度的重要指标，经常用于聚类效果评估等场景。

NMI 的值域为 \([0,1]\)：\(0\) 表示两个结果完全独立，\(1\) 表示两个结果完全一致。

\[\text{NMI(Y,C)}=\frac{2\times I\text{(Y;C)}}{H\text{(Y)}+H\text{(C)}} \]

• \(\text{Y}\)代表数据真实的类别；\(\text{C}\) 表示聚类的结果。
• \(H(\cdot)\) 表示信息熵，\(H(X)=-\sum_{i=1}^N p(i)\log\ p(i)\)。
• \(I(Y;C)\) 代表互信息， \(I(Y;C)=H(Y)-H(Y|C)\) 。

从信息论的角度分析一下，\(H\text{(Y)}\) 表示真实分类的信息量；\(H\text{(C)}\) 表示聚类的信息量；\(I\text{(Y;C)}\) 表示两者的重叠信息量；\(\text{NMI}\)表示聚类结果与真实标签共享了多少比例的信息，越接近 1 表示聚类越靠谱。

例子

假设有20个样本，真实分成3类 (\(\text{Y}\))，聚类结果分2类 (\(\text{C}\))。如下：

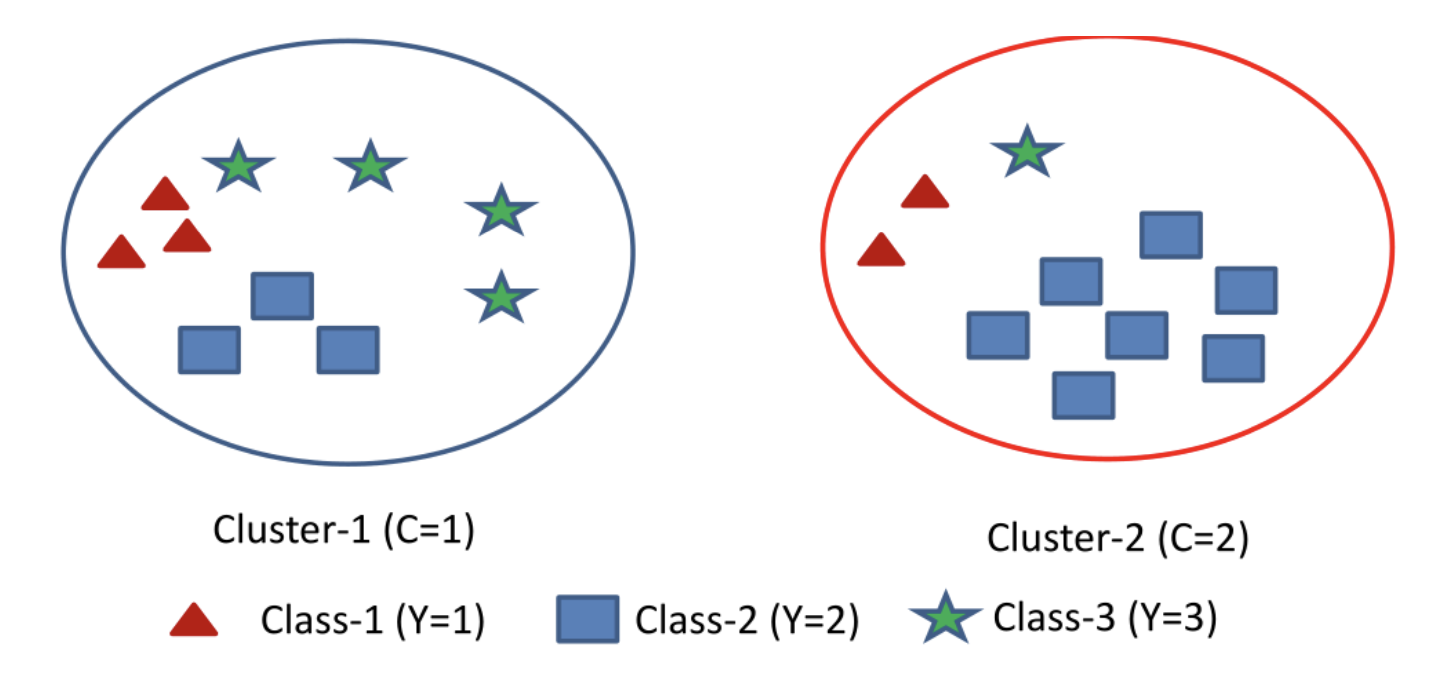
1. 计算 \(Y\) 的信息熵 \(H(Y)\)

   H(Y) 表示数据真实标签的熵，是一个固定的值，可以在聚类之前计算出。

   \[\begin{split} H(Y)&=-\sum_{y=1}^3 P(Y=y)logP(Y=y)\\ &=-(\frac{1}{4}log(\frac{1}{4})+\frac{1}{4}log(\frac{1}{4})+\frac{1}{2}log(\frac{1}{2}))\\ &=1.5\ bit \end{split} \]

2. 计算 \(C\) 的信息熵

   \[\begin{split} H(C)&=-\sum_{c=1}^3 P(C=c)logP(C=c)\\ &=-(\frac{1}{2}log(\frac{1}{2})+\frac{1}{2}log(\frac{1}{2}))\\ &=1\ bit \end{split} \]

3. 计算 \(Y\) 和 \(C\) 的互信息

   \[\begin{split} H(Y|C)&=H(Y|C=1)+H(Y|C=2)\\ &=-\sum_{c=1}^2P(C=c)\sum_{y=1}^3 P(Y=y|C=c)logP(Y=y|C=c)\\ &=1.3639\ bit \end{split} \]
   \[\begin{split} I(Y;C)&=H(Y)-H(Y|C)\\ &=1.5-1.3639\\ &=0.1361\ bit \end{split} \]

4. 计算 \(Y\) 和 \(C\) 的归一化互信息

\[\begin{split} \text{NMI(Y,C)}&=\frac{2\times I(Y;C)}{H(Y)+H(C)}\\ &=0.1089 \end{split} \]

通过上面的例子，可以大致学会计算NMI，同时可以分析一下各个参数的含义：

• 真实类别的信息熵 \(H(Y) = 1.5\)，表示这组真实分类的信息量较大，即分类本身分布较均匀，复杂度不低；
• 聚类结果的信息熵 \(H(C) = 1\)，表示聚类算法对数据进行了某种划分，但划分结构较简单；
• 条件熵 \(H(Y|C) \approx 1.36\)，说明即使知道聚类结果 \(C\)，我们对真实标签 \(Y\) 的不确定性仍然很高；
• 最终互信息 \(I(Y;C) \approx 0.1361\)，仅占总信息量的很小一部分；
• 归一化互信息 \(NMI \approx 0.1089\)，表示聚类结构与真实类别几乎没有太强的相关性，聚类效果较差。

为什么“归一化”互信息

可以观察到，此例子中的互信息也很小，可以直接当作聚类效果的评价指标，为什么要对其进行归一化多此一举呢？

​ 互信息 \(I(Y;C)\) 本身可以理解为\(Y,C\)重叠的信息量，其数值受类别数量显著影响；如果 \(Y\) 和 \(C\) 的类别数都大幅增加（信息量基数增大），即使匹配得不太好，\(I(Y;C)\) 的数值也可能看起来更大。因此，\(I(Y;C)\) 是一个“绝对量”，在不同任务、不同类别数下难以直接对比， 而使用NMI将互信息标准化到 \([0,1]\) 区间内，使其具有可比较性。