♠ JavaScript数据结构与算法之算法
排序介绍
排序算法有很多: 冒泡排序/选择排序/插入排序/归并排序/计数排序(counting sort)/基数排序(radix sort)/希尔排序/堆排序/桶排序.
- 简单排序: 冒泡排序 - 选择排序 - 插入排序
- 高级排序: 希尔排序 - 快速排序

冒泡排序
冒泡排序算法相对其他排序运行效率较低, 但是在概念上它是排序算法中最简单的.
冒泡排序的思路:
- 对未排序的各元素从头到尾依次比较相邻的两个元素大小关系
- 如果左边的队员高, 则两队员交换位置
- 向右移动一个位置, 比较下面两个队员
- 当走到最右端时, 最高的队员一定被放在了最右边
- 按照这个思路, 从最左端重新开始, 这次走到倒数第二个位置的队员即可.
- 依次类推, 就可以将数据排序完成

思路再分析:
- 第一次找出最高人放在最后, 我们需要两个两个数据项进行比较, 那么这个应该是一个循环操作.
- 第二次将次高的人找到放在倒数第二个位置, 也是两个比较, 只是不要和最后一个比较(少了一次), 但是前面的两个两个比较也是一个循环操作.
- 第三次...第四次...
- 有发现规律吗? 这应该是一个循环中嵌套循环, 并且被嵌套的循环次数越来越少的.
- 根据这个分析, 你能写出代码实现吗?
代码解析:
点击查看代码
ArrayList.prototype.bubbleSort = function () {
// 1.获取数组的长度
var length = this.array.length
// 2.反向循环, 因此次数越来越少
for (var i = length - 1; i >= 0; i--) {
// 3.根据i的次数, 比较循环到i位置
for (var j = 0; j < i; j++) {
// 4.如果j位置比j+1位置的数据大, 那么就交换
if (this.array[j] > this.array[j+1]) {
// 交换
this.swap(j, j+1)
}
}
}
}
ArrayList.prototype.swap = function (m, n) {
var temp = this.array[m]
this.array[m] = this.array[n]
this.array[n] = temp
}- 代码序号1: 获取数组的长度.
- 代码序号2: 我们现在要写的外层循环, 外层循环应该让i依次减少, 因此我们这里使用了反向的遍历.
- 代码需要3: 内层循环, 内层循环我们使用 j < i. 因为上面的i在不断减小, 这样就可以控制内层循环的次数.
- 代码需要4: 比较两个数据项的大小, 如果前面的大, 那么就进行交换.
冒泡排序的效率
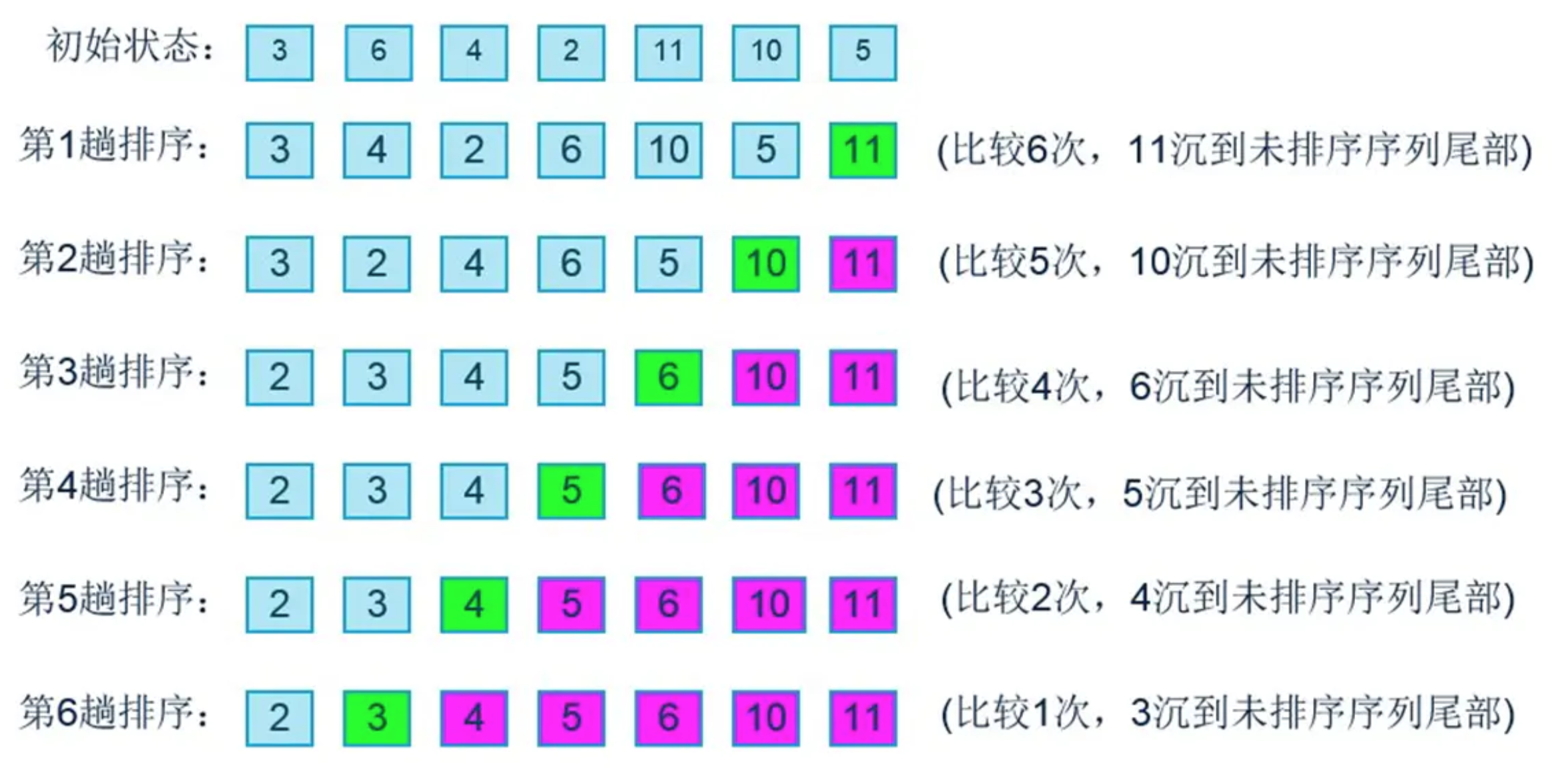
冒泡排序的比较次数:
- 如果按照上面的例子来说, 一共有7个数字, 那么每次循环时进行了几次的比较呢?
- 第一次循环6次比较, 第二次5次比较, 第三次4次比较....直到最后一趟进行了一次比较.
- 对于7个数据项比较次数: 6 + 5 + 4 + 3 + 2 + 1
- 对于N个数据项呢? (N - 1) + (N - 2) + (N - 3) + ... + 1 = N * (N - 1) / 2
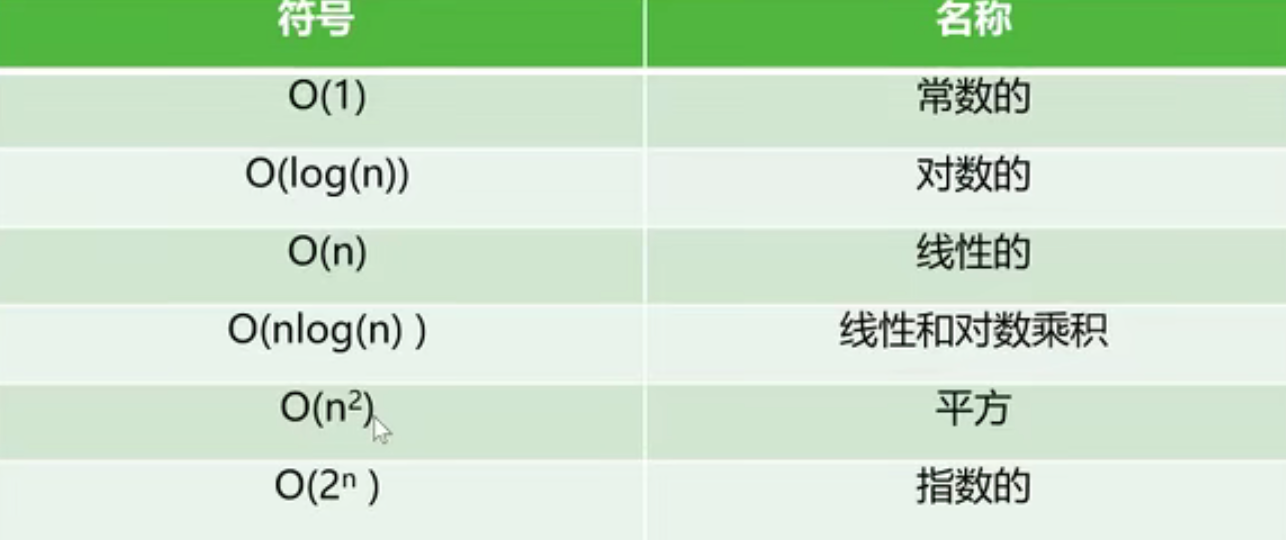
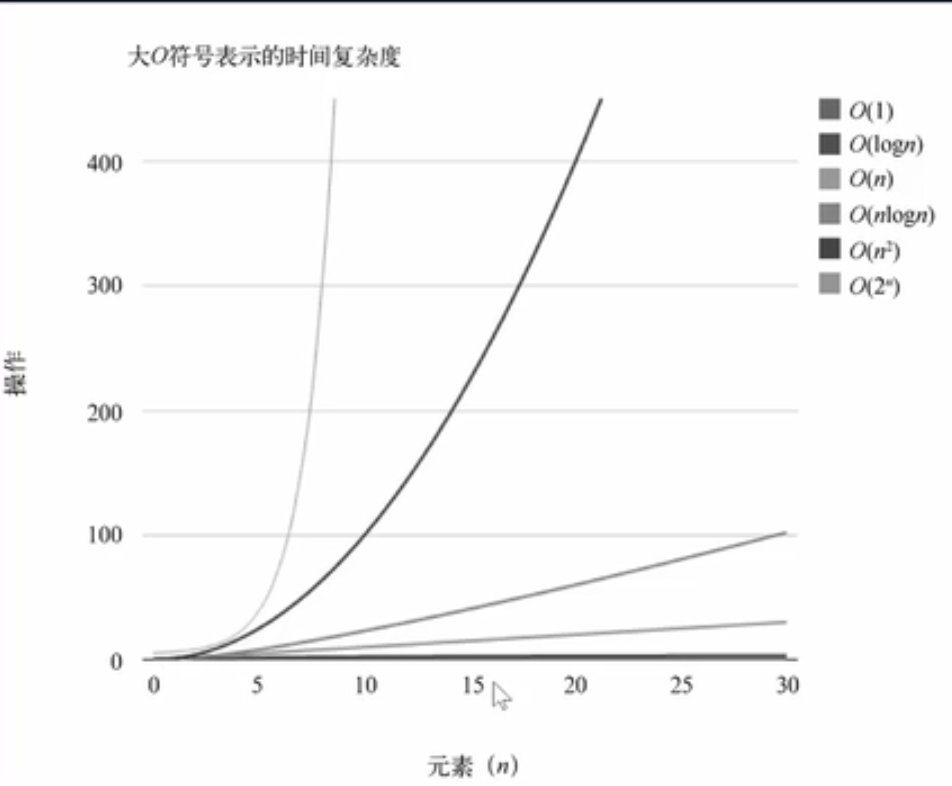
大O表示法,大O表示法是描述性能和复杂度的一种表示方法.推导大O表示法通常我们会使用如下规则:
- 用常量1取代运行时间中的所有加法常量
- 在修改后的运行次数函数中, 只保留最高阶项
- 如果最高阶项存在并且不是1, 则去除与这个项相乘的常数.
通过大O表示法推到过程, 我们来推到一下冒泡排序的大O形式.
- N * (N - 1) / 2 = N²/2 - N/2,根据规则2, 只保留最高阶项, 编程N² / 2
- N² / 2, 根据规则3, 去除常量, 编程N²
- 因此冒泡排序的大O表示法为O(N²)
冒泡排序的交换次数:
- 如果有两次比较才需要交换一次(不可能每次比较都交换一次.), 那么交换次数为N² / 4
- 由于常量不算在大O表示法中, 因此, 我们可以认为交换次数的大O表示也是O(N²)
选择排序
选择排序改进了冒泡排序, 将交换的次数由O(N²)减少到O(N), 但是比较的次数依然是O(N²)
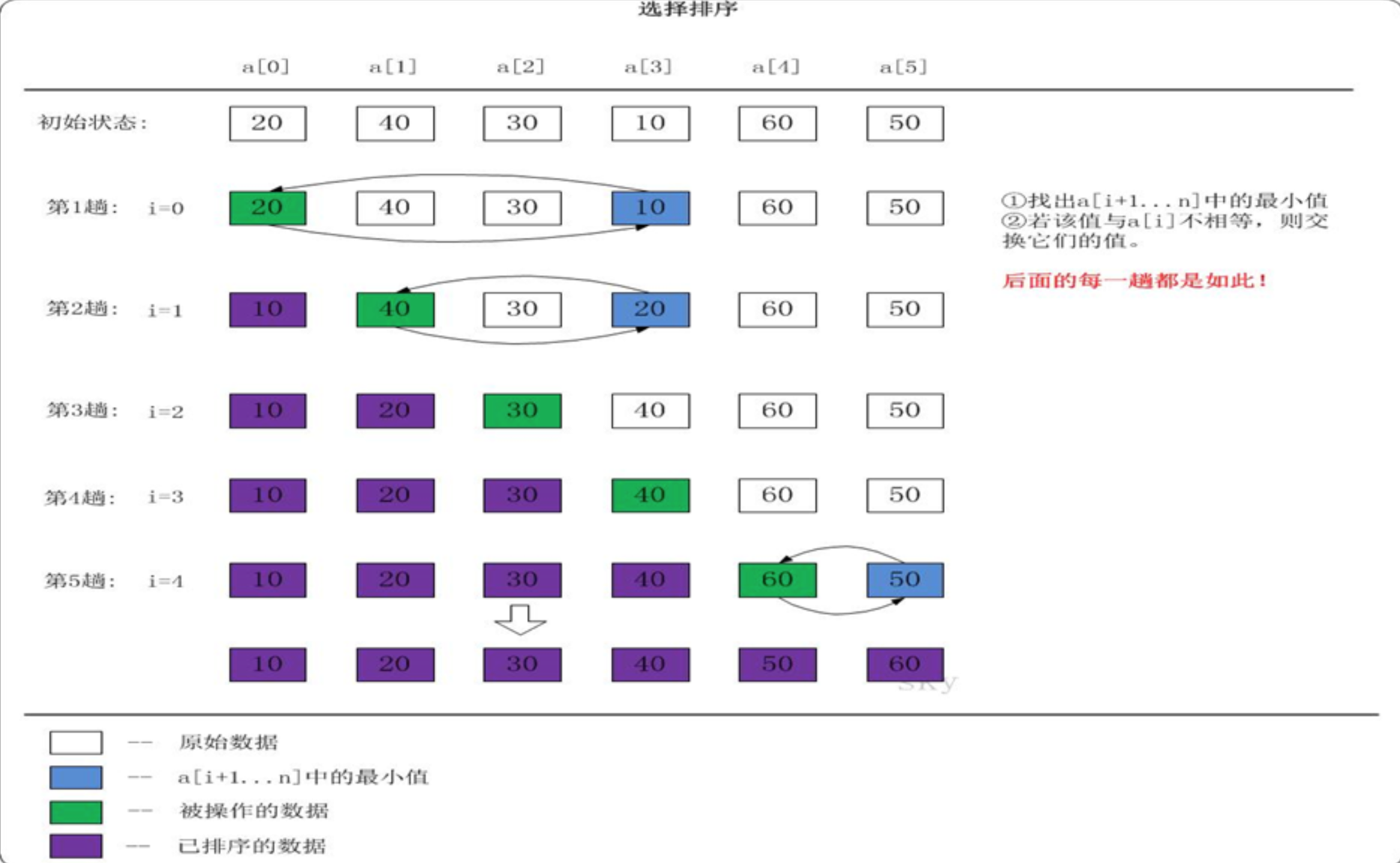
选择排序的思路:
- 选定第一个索引位置,然后和后面元素依次比较
- 如果后面的队员, 小于第一个索引位置的队员, 则交换位置
- 经过一轮的比较后, 可以确定第一个位置是最小的
- 然后使用同样的方法把剩下的元素逐个比较即可
- 可以看出选择排序,第一轮会选出最小值,第二轮会选出第二小的值,直到最后
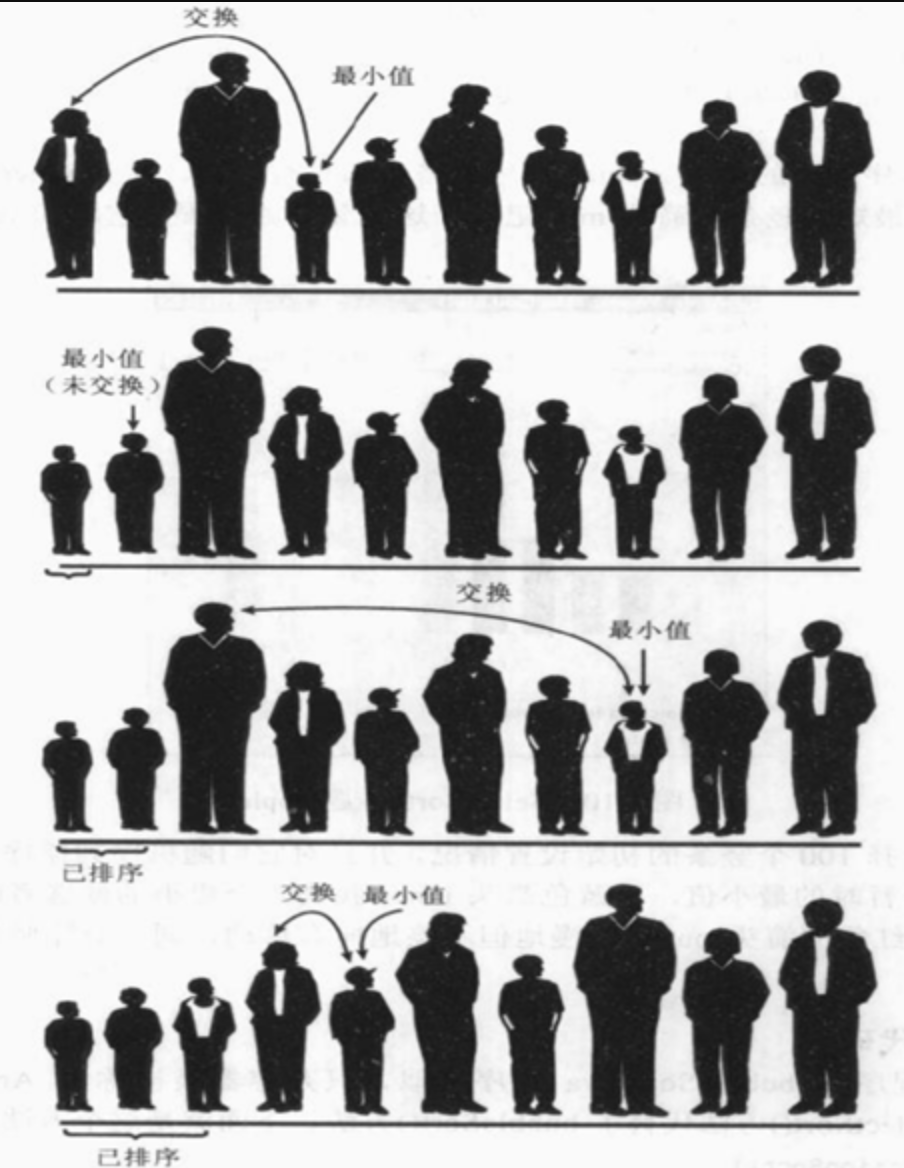
- 选择排序第一次将第0位置的人取出, 和后面的人(1, 2, 3...)依次比较, 如果后面的人更小, 那么就交换.
- 这样经过一轮之后, 第一个肯定是最小的人.
- 第二次将第1位置的人取出, 和后面的人(2, 3, 4...)依次比较, 如果后面的人更小, 那么就交换.
- 这样经过第二轮后, 第二个肯定是次小的人.
- 第三轮...第四轮...直到最后就可以排好序了. 有发现规律吗?
- 外层循环依次取出0-1-2...N-2位置的人作为index(N-1不需要取了, 因为只剩它一个了肯定是排好序的)
- 内层循环从index+1开始比较, 直到最后一个.
代码解析:
点击查看代码
ArrayList.prototype.selectionSort = function () {
// 1.获取数组的长度
var length = this.array.length
// 2.外层循环: 从0位置开始取出数据, 直到length-2位置
for (var i = 0; i < length - 1; i++) {
// 3.内层循环: 从i+1位置开始, 和后面的内容比较
var min = i
for (var j = min + 1; j < length; j++) {
// 4.如果i位置的数据大于j位置的数据, 那么记录最小的位置
if (this.array[min] > this.array[j]) {
min = j
}
}
// 5.交换min和i位置的数据
this.swap(min, i)
}
}- 代码序号1: 依然获取数组的长度.
- 代码序号2: 外层循环, 我们已经讲过, 需要从外层循环的第0个位置开始, 依次遍历到length - 2的位置.
- 代码序号3: 先定义一个min, 用于记录最小的位置, 内层循环, 内层循环是从i+1位置开始的数据项, 和i位置的数据项依次比较, 直到length-1的数据项.
- 代码序号4: 如果比较的位置i的数据项, 大于后面某一个数据项, 那么记录最小位置的数据.
- 代码序号5: 将min位置的数据, 那么i位置的数据交换, 那么i位置就是正确的数据了.
- 注意: 这里的交换是基于之前的交换方法, 这里直接调用即可.
选择排序的效率
选择排序的比较次数:
选择排序和冒泡排序的比较次数都是N*(N-1)/2, 也就是O(N²).
选择排序的交换次数:
- 选择排序的交换次数只有N-1次, 用大O表示法就是O(N).
- 所以选择排序通常认为在执行效率上是高于冒泡排序的.
插入排序
插入排序是简单排序中效率最好的一种.插入排序也是学习其他高级排序的基础, 比如希尔排序/快速排序, 所以也非常重要.
插入排序的思路
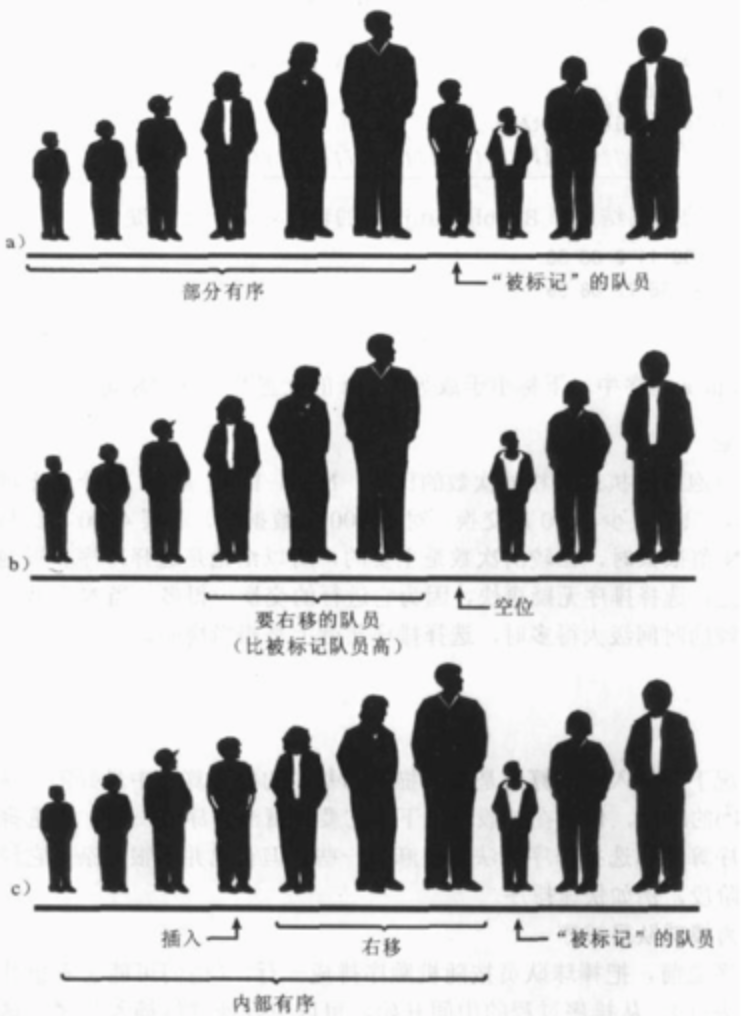
局部有序:
- 插入排序思想的核心是局部有序. 什么是局部有序呢?
- 比如在一个队列中的人, 我们选择其中一个作为标记的队员. 这个被标记的队员左边的所有队员已经是局部有序的.
- 这意味着, 有一部门人是按顺序排列好的. 有一部分还没有顺序.
插入排序的思路:
- 从第一个元素开始,该元素可以认为已经被排序
- 取出下一个元素,在已经排序的元素序列中从后向前扫描
- 如果该元素(已排序)大于新元素,将该元素移到下一位置
- 重复上一个步骤,直到找到已排序的元素小于或者等于新元素的位置
- 将新元素插入到该位置后, 重复上面的步骤.
- 插入排序应该从下标值1开始(因为0位置默认可以被认为是有序的)
- 从1位置开始取出元素, 并且判断该元素的大小和0位置进行比较, 如果1位置元素小于0位置元素, 那么交换, 否则不交换.
- 上面步骤执行完成后, 0 - 1位置已经排序好.
- 取出2位置的元素, 和1位置进行比较:
- 如果2位置元素大于1位置元素, 说明2位置不需要任何动作. 0 - 1 - 2已经排序好.
- 如果2位置元素小于1位置元素, 那么将1移动到2的位置, 并且2继续和0进行比较.
- 如果2位置元素大于0位置的元素, 那么将2位置放置在1的位置, 排序完成. 0 - 1 - 2搞定.
- 如果2位置元素小于0位置的元素, 那么将0位置的元素移动到1位置, 并且将2位置的元素放在0位置, 0 - 1 - 2搞定.
- 按照上面的步骤, 依次找到最后一个元素, 整个数组排序完成.
代码解析
点击查看代码
ArrayList.prototype.insertionSort = function () {
// 1.获取数组的长度
var length = this.array.length
// 2.外层循环: 外层循环是从1位置开始, 依次遍历到最后
for (var i = 1; i < length; i++) {
// 3.记录选出的元素, 放在变量temp中
var j = i
var temp = this.array[i]
// 4.内层循环: 内层循环不确定循环的次数, 最好使用while循环
while (j > 0 && this.array[j-1] > temp) {
this.array[j] = this.array[j-1]
j--
}
// 5.将选出的j位置, 放入temp元素
this.array[j] = temp
}
}- 代码序号1: 获取数组的长度.
- 代码序号2: 外层循环, 从1位置开始, 因为0位置可以默认看成是有序的了.
- 代码序号3: 记录选出的i位置的元素, 保存在变量temp中. i默认等于j
- 代码序号4: 内层循环
- 内层循环的判断j - 1位置的元素和temp比较, 并且j > 0.
- 那么就将j-1位置的元素放在j位置.
- j位置向前移.
- 代码序号5: 将目前选出的j位置放置temp元素.
插入排序的效率
- 插入排序的比较次数:
- 第一趟时, 需要的最多次数是1, 第二趟最多次数是2, 依次类推, 最后一趟是N-1次.
- 因此是1 + 2 + 3 + ... + N - 1 = N * (N - 1) / 2.
- 然而每趟发现插入点之前, 平均只有全体数据项的一半需要进行比较.
- 我们可以除以2得到 N * (N - 1) / 4. 所以相对于选择排序, 其他比较次数是少了一半的.
- 插入排序的复制次数:
- 第一趟时, 需要的最多复制次数是1, 第二趟最多次数是2, 依次类推, 最后一趟是N-1次.
- 因此是1 + 2 + 3 + ... + N - 1 = N * (N - 1) / 2.
- 平均 N * (N - 1) / 4
- 对于基本有序的情况
- 对于已经有序或基本有序的数据来说, 插入排序要好很多.
- 当数据有序的时候, while循环的条件总是为假, 所以它变成了外层循环中的一个简单语句, 执行N-1次.
- 在这种情况下, 算法运行至需要N(N)的时间, 效率相对来说会更高.
- 另外别忘了, 我们的比较次数是选择排序的一半, 所以这个算法的效率是高于选择排序的.
希尔排序
希尔排序的思路
回顾插入排序:
- 由于希尔排序基于插入排序, 所以有必须回顾一下前面的插入排序.
- 我们设想一下, 在插入排序执行到一半的时候, 标记符左边这部分数据项都是排好序的, 而标识符右边的数据项是没有排序的.
- 这个时候, 取出指向的那个数据项, 把它存储在一个临时变量中, 接着, 从刚刚移除的位置左边第一个单元开始, 每次把有序的数据项向右移动一个单元, 直到存储在临时变量中的数据项可以成功插入.
插入排序的问题:
- 假设一个很小的数据项在很靠近右端的位置上, 这里本来应该是较大的数据项的位置.
- 把这个小数据项移动到左边的正确位置, 所有的中间数据项都必须向右移动一位.
- 如果每个步骤对数据项都进行N次复制, 平均下来是移动N/2, N个元素就是 N*N/2 = N²/2.
- 所以我们通常认为插入排序的效率是O(N²)
- 如果有某种方式, 不需要一个个移动所有中间的数据项, 就能把较小的数据项移动到左边, 那么这个算法的执行效率就会有很大的改进.
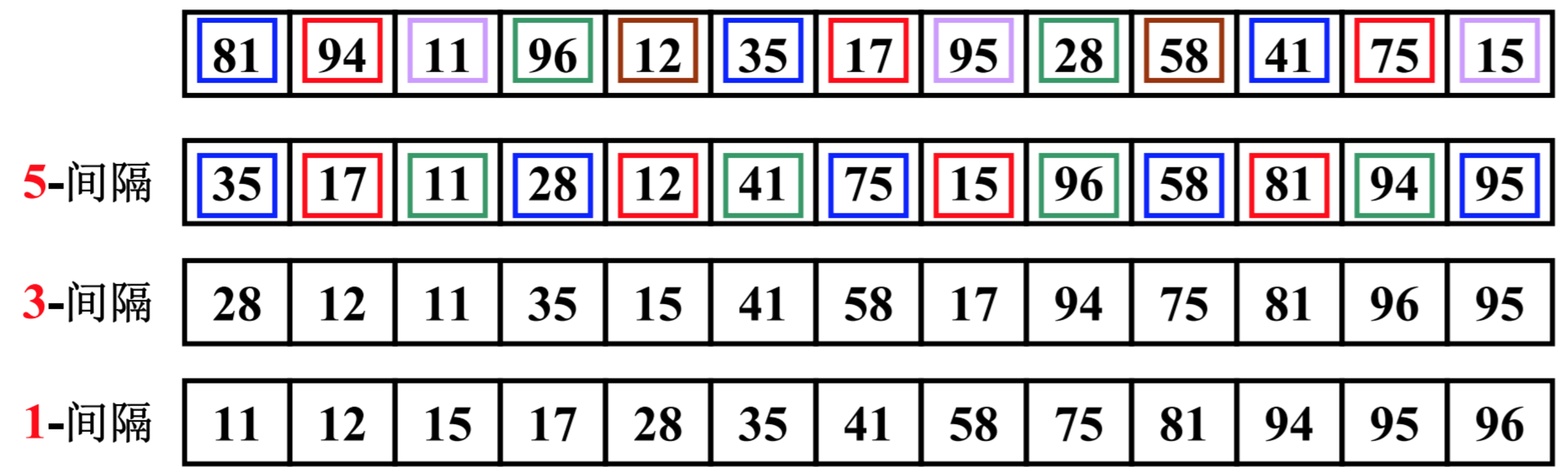
希尔排序的做法:
- 比如下面的数字, 81, 94, 11, 96, 12, 35, 17, 95, 28, 58, 41, 75, 15.
- 我们先让间隔为5, 进行排序. (35, 81), (94, 17), (11, 95), (96, 28), (12, 58), (35, 41), (17, 75), (95, 15)
- 排序后的新序列, 一定可以让数字离自己的正确位置更近一步.
- 我们再让间隔位3, 进行排序. (35, 28, 75, 58, 95), (17, 12, 15, 81), (11, 41, 96, 94)
- 排序后的新序列, 一定可以让数字离自己的正确位置又近了一步.
- 最后, 我们让间隔为1, 也就是正确的插入排序. 这个时候数字都离自己的位置更近, 那么需要复制的次数一定会减少很多.
选择合适的增量:
- 在希尔排序的原稿中, 他建议的初始间距是N / 2, 简单的把每趟排序分成两半.
- 也就是说, 对于N = 100的数组, 增量间隔序列为: 50, 25, 12, 6, 3, 1.
- 这个方法的好处是不需要在开始排序前为找合适的增量而进行任何的计算.
- 我们先按照这个增量来实现我们的代码.
代码解析
点击查看代码
ArrayList.prototype.shellSort = function () {
// 1.获取数组的长度
var length = this.array.length
// 2.根据长度计算增量
var gap = Math.floor(length / 2)
// 3.增量不断变量小, 大于0就继续排序
while (gap > 0) {
// 4.实现插入排序
for (var i = gap; i < length; i++) {
// 4.1.保存临时变量
var j = i
var temp = this.array[i]
// 4.2.插入排序的内层循环
while (j > gap - 1 && this.array[j - gap] > temp) {
this.array[j] = this.array[j - gap]
j -= gap
}
// 4.3.将选出的j位置设置为temp
this.array[j] = temp
}
// 5.重新计算新的间隔
gap = Math.floor(gap / 2)
}
}- 代码序号1: 获取数组的长度
- 代码序号2: 计算第一次的间隔, 我们按照希尔提出的间隔实现.
- 代码序号3: 增量不断变小, 大于0就继续改变增量
- 代码序号4: 实际上就是实现了插入排序
- 代码序号4.1: 保存临时变量, j位置从i开始, 保存该位置的值到变量temp中
- 代码序号4.2: 内层循环, j > gap - 1并且temp大于this.array[j - gap], 那么就进行复制.
- 代码序号4.3: 将j位置设置为变量temp
- 代码序号5: 每次while循环后都重新计算新的间隔.
希尔排序的效率
希尔排序的效率
- 希尔排序的效率很增量是有关系的.
- 但是, 它的效率证明非常困难, 甚至某些增量的效率到目前依然没有被证明出来.
- 但是经过统计, 希尔排序使用原始增量, 最坏的情况下时间复杂度为O(N²), 通常情况下都要好于O(N²)
Hibbard 增量序列
- 增量的算法为2^k - 1. 也就是为1 3 5 7...等等.
- 这种增量的最坏复杂度为O(N^3/2), 猜想的平均复杂度为O(N^5/4), 目前尚未被证明.
Sedgewick增量序列
- {1, 5, 19, 41, 109, … }, 该序列中的项或者是94^i - 9*2^i + 1或者是4^i - 32^i + 1
- 这种增量的最坏复杂度为O(N^4/3), 平均复杂度为O(N^7/6), 但是均未被证明.
总之, 我们使用希尔排序大多数情况下效率都高于简单排序, 甚至在合适的增量和N的情况下, 还好好于快速排序.
快速排序
快速排序的思路
快速排序几乎可以说是目前所有排序算法中, 最快的一种排序算法.
当然, 没有任何一种算法是在任意情况下都是最优的, 比如希尔排序确实在某些情况下可能好于快速排序. 但是大多数情况下, 快速排序还是比较好的选择.
快速排序的重要性:
- 如果有一天你面试的时候, 让你写一个排序算法, 你可以洋洋洒洒的写出多个排序算法, 但是如果其中没有快速排序, 那么证明你对排序算法也只是浅尝辄止, 并没有深入的研究过.
- 因为快速排序可以说是排序算法中最常见的, 无论是C++的STL中, 还是Java的SDK中其实都能找到它的影子.
- 快速排序也被列为20世纪十大算法之一.
快速排序是什么?
- 希尔排序相当于插入排序的升级版, 快速排序其实是我们学习过的最慢的冒泡排序的升级版.
- 我们知道冒泡排序需要经过很多次交换, 才能在一次循环中, 将最大值放在正确的位置.
- 而快速排序可以在一次循环中(其实是递归调用)找出某个元素的正确位置, 并且该元素之后不需要任何移动.
快速排序的思想:
快速排序最重要的思想是分而治之.
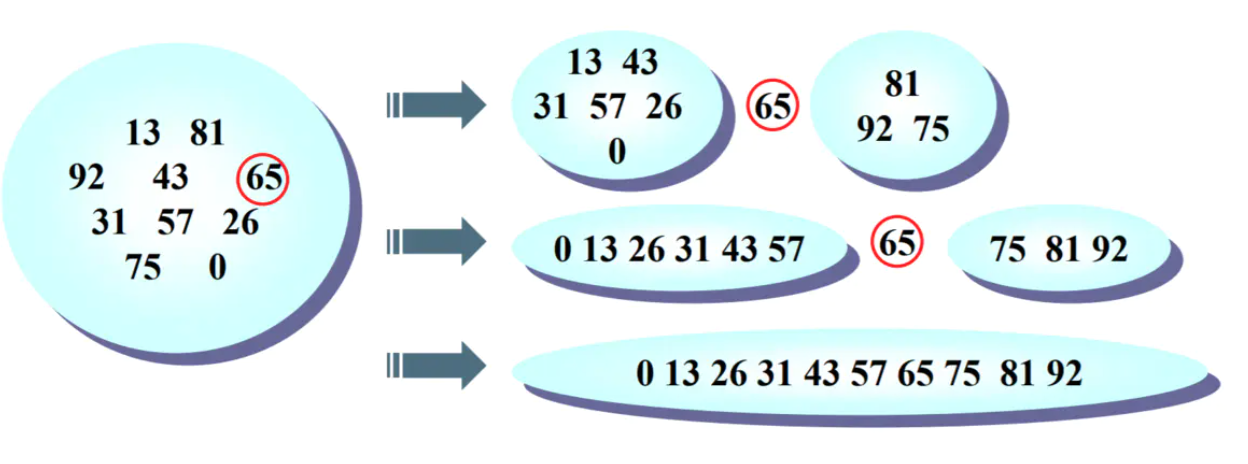
比如我们下面有这样一顿数字需要排序:
- 第一步: 从其中选出了65. (其实可以是选出任意的数字, 我们以65举个栗子)
- 第二步: 我们通过算法: 将所有小于65的数字放在65的左边, 将所有大于65的数字放在65的右边.
- 第三步: 递归的处理左边的数据.(比如你选择31来处理左侧), 递归的处理右边的数据.(比如选择75来处理右侧, 当然选择81可能更合适)
- 最终: 排序完成
和冒泡排序不同的是什么呢?
- 我们选择的65可以一次性将它放在最正确的位置, 之后不需要任何移动.
- 需要从开始位置两个两个比较, 如果第一个就是最大值, 它需要一直向后移动, 直到走到最后.
- 也就是即使已经找到了最大值, 也需要不断继续移动最大值. 而插入排序对数字的定位是一次性的.
在快速排序中有一个很重要的步骤就是选取枢纽(pivot也人称为主元).如何选择才是最合适的枢纽呢?
- 一种方案是直接选择第一个元素作为枢纽.但第一个作为枢纽在某些情况下, 效率并不是特别高.
- 另一种方案是使用随机数:随机取 pivot?但是随即函数本身就是一个耗性能的操作.
- 另一种比较优秀的解决方案: 取头、中、尾的中位数
快速排序的效率
快速排序的最坏情况效率
- 什么情况下会有最坏的效率呢? 就是每次选择的枢纽都是最左边或者最后边的.
- 那么效率等同于冒泡排序.
- 而我们的例子可能有最坏的情况吗? 是不可能的. 因为我们是选择三个值的中位值.
快速排序的平均效率:
- 快速排序的平均效率是O(N * logN).
- 虽然其他某些算法的效率也可以达到O(N * logN), 但是快速排序是最好的.


 浙公网安备 33010602011771号
浙公网安备 33010602011771号