利用Multisim设计WCF架构电子管耳放-第二部分

第二部分 选择输出管的工作点，并进行仿真

由于耳放在最大60mw，120欧负载情况下的输出电压峰-峰值有7.59V，交流电流的峰-峰值有63.25mA，假设上下每个管子输出一半，那么每个管子的有效负载就是120*2=240欧，输出电流的峰-峰值大于63.25/2=31.625mA。选择Ia>20mA，应该可以满足要求。输出管工作点在选择的时候注意考虑以下几点：

1. 输出功率不要超屏耗。 6N6的屏耗Pmax=4.8W

2. 满幅输出时，失真度尽量小。也就是输出电流的正负半周尽量对称；

由于利用Multisim IV仪得到的特性曲线没有刻度，很难做负载线。但可以利用基本的共阴电路来确定工作点是否合适；

第一步 求出工作点附近的管子参数

设置IV分析仪中NMOS管的仿真参数：

• V_ds，相当于Ua：开始：0V，结束：300V，增量：1V

• V_gs：相当于Ug：开始：-4.5V，结束：0V，步数：10；以0.5V为间隔，测试从-4.5到0V共10条曲线；

自动测试后，调整曲线的电流范围和电压范围，得到比较容易观测的图形。

点击V_gs=-3.5V的曲线，右键弹出菜单，选择“显示选择标志”，就可以看到被选中的曲线有“∆”符合标识；拖到V_ds测量线到135V，此时显示出工作点的电流为22.456mA。此时的屏耗=135*22.456/1000=3.03w，小于Pmax。

V_ds测量线和V_gs=-3.5的交点就是工作点Q。如下图所示：

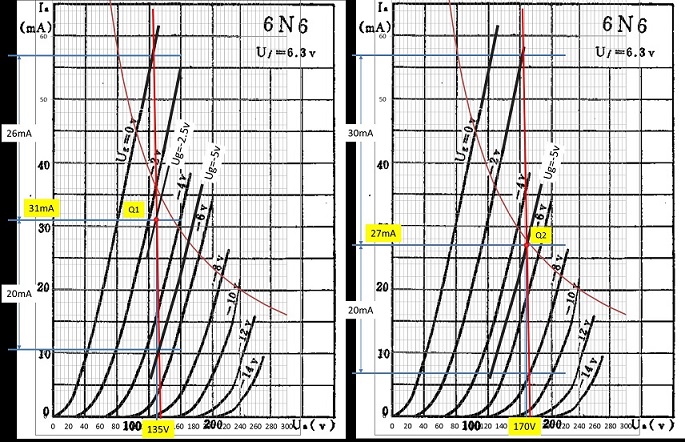
图5：工作点Q1：V_ds=135V, V_gs=-3.5V

保持V_ds选择线不变，选择V_gs=-3V的曲线，此时显示的电流为26.692mA，再选择V_gs=-4V的曲线，此时显示的电流为18.597mA，那么管子在Q1的跨导：

\(gm=\frac{26.692-18.597}{4-3}=8.10\)

选择V_gs=-3V的曲线，拖动V_ds选择线，使得电流显示最接近22.465mA，记录此时的电压值为126.745V；再选择V_gs=4V的曲线，拖动V_ds选择线，使得电流显示最接近22.465mA，记录此时的电压值为143.212V；那么管子在Q1的放大系数为：

\(µ = \frac{143.212-126.745}{4-3} = 16.47\)

则管子在Q1的内阻为：

\(ra = \frac {µ}{gm} = \frac {16.47}{8.10} = 2.03( KΩ)\)

考虑RL=240欧时的测试电路，此时：

\(Rk = \frac {3.5V}{22.456mA} = 0.16k\)

\(HT(V) = 135 + (0.24+0.16)*22.456 = 143.89(V)\)

搭共阴测试电路如下图：

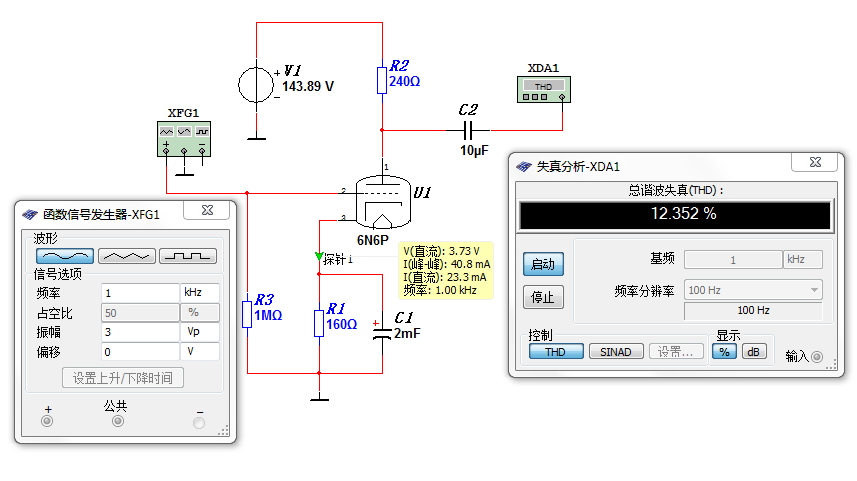
图6 共阴测试电路

可见在负载只有240欧，输出电流\(I_{pp}=40.8mA\)时，失真度达到12.352%。这也说明共阴电路是不适合驱动重负载的。不过，在实际的WCF电路中，由于存在深度负反馈，失真应该不会这么大。

第二步 在Multisim里搭建WCF电路

先不考虑驱动级。用两个分压电阻代替驱动级，给WCF电路上管提供偏压。为了便于调试，在电路里增加了信号发生器，输出功率计，输出电压探针和失真度仪。

为了比较上下管的输出，给上下管增加了1欧的取样电阻；

为了测试输出阻抗，还增加了额外的负载和控制开关。

测试电路如下图所示：

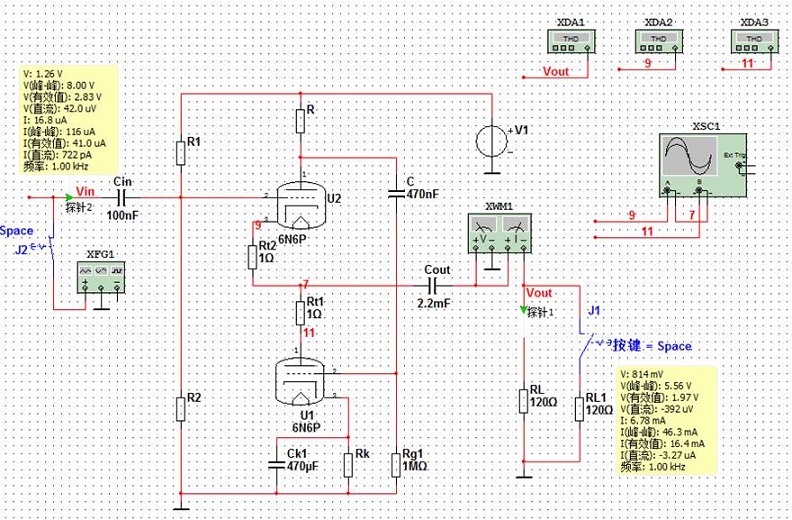
图7 WFC测试电路

根据选定的工作点，需要计算的元件有下管的阴极电阻Rk，分压电阻R1，R2，HT， 还有上管的阳极电阻R。Cout的值在测出输出阻抗后再确定；

取工作点是\(Ug=-3.5V， Ua=135V， Ia=22.456mA\)，则：

\(Rk = \frac {3.5}{22.456} = 0.16 (KΩ)，Power\_Rk=\frac {3.5*22.456}{1000} = 0.08(W)\)

R的取值会影响HT，进而影响分压电路的计算。所以有必要先对R的值进行估算。看到有的文章里说当R=1/gm时，失真度最小。但都没有给出理由和推导过程。我尝试对这个结果进行推导：

由于上管和下管构成了推挽输出。上管阴极输出电流的方向和下管阳极输出电流的方向相反，叠加在一起后一起驱动负载。

假设要使叠加后的信号失真最小，那么上下管的输出电流，应该大小相等，方向相同。

上下管输出最大电流的时候，就是负载为0的时候；可以画出这时候的电路交流通路，如下图：

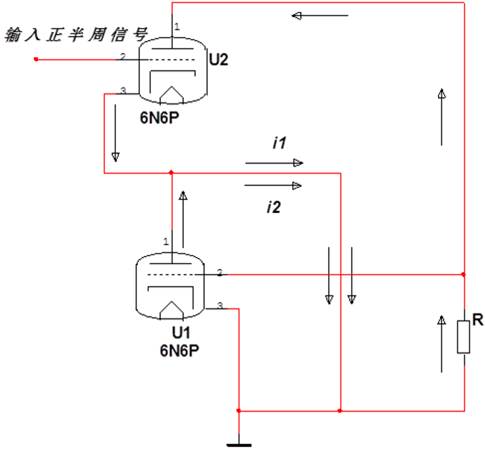
图8 WFC等效电路-1

图中所示是输出正半周信号的时候，电路中电流的流向。当上下管平衡的时候：

\(i1=i2\) -----------------------------------(1)

\(i2\)是由于\(i1\)在R上产生压降，经U1放大后产生的，因此根据电子管基本特性，\(i2\)和\(i1\)还满足下面的关系：

\(i2=gm * i1 * R\)--------------------------(2)

(1) 代入(2) 得：\(i2 = gm* i2 * R\)

所以: \(R=\frac{1}{gm}\)

考虑负载RL不为0的情况。那么交流通路就如下图：

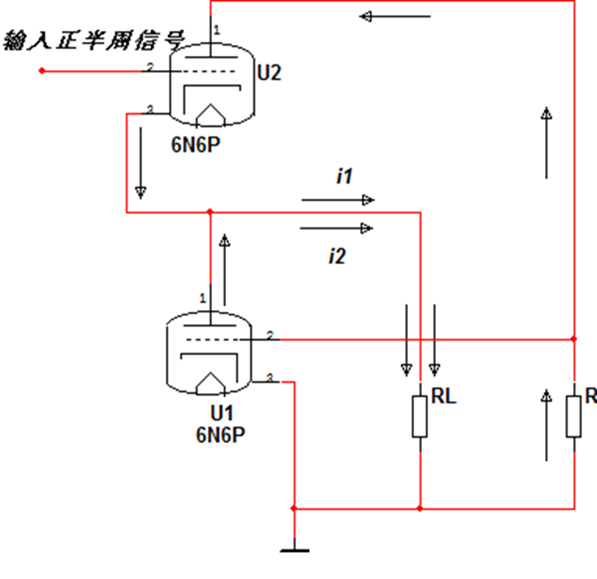
图9：WFC等效电路-2

由于\(i1=i2\)，那么RL对于下管U1 来说等效阻抗就为2*RL，利用三极管电流方程，可以得到如下\(i2\)和\(i1\)的关系：

\(i2 = µ * \frac{i1 * R}{ra + 2RL}，µ为U1的放大系数，ra为U1 的内阻\)

可以计算出 : \(R = \frac{1}{gm} + \frac{2RL}{µ}\)

也就是说R的最优值不仅和下管内阻有关，而且和负载阻抗有关。

但在实际仿真测试时，R取计算值时，失真并不是最小。但可以把计算值作为基准值，通过调整得到失真最小的最优值；

因此可以先按照\(R = \frac{1}{gm} + \frac{2RL}{µ}\)计算：

\(R = \frac{1}{8.10} + \frac {2*120}{16.47} = 0.138 (KΩ)\)

\(HT = 2 * Ua + Ia * (Rk + R) = 2 * 135+ 22.456*(0.16+0.138)=276.7(V)\)

分压电路的电流取1mA，上下管工作状态一致。分压电路要保证上管U2的栅极电压比阴极电压低2.5V。U2的阴极电压为\(Ua+Ug=130+2.5=132.5(V)\)，所以U2的栅极电压应当为130V

\(R2 = \frac{130V}{1mA} =130(KΩ)\)

\(R1 = \frac{276V}{1mA} – 130 = 146(KΩ)\)

第三步 开始仿真测试

首先给电路输入1khz的正弦波，并观测输出的功率表，保证在120欧的负载上输出60mw左右的功率。

然后调整不同的R值分别进行测试。每次测试都保证输出功率在60mw左右。严格来讲，R值改变，HT和分压电阻R1的值需要重新计算，并调整。实际测的时候，发现影响不是很大。

最终确定R=185欧时，失真最小。重新计算一下HT=278V，R1=148(KΩ)。

当输出60mw功率时，失真度为0.19%

当输出20mw功率时，失真度为0.062%

测试电路及结果如下图：

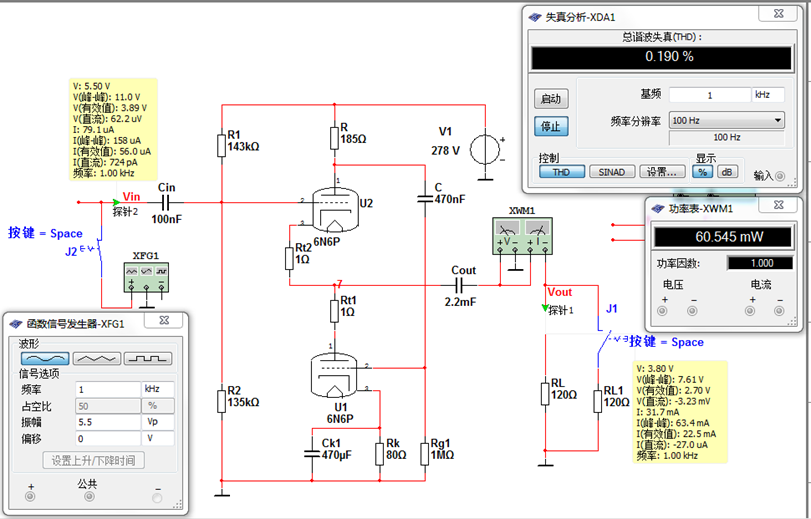
图10 输出60mw的测试结果

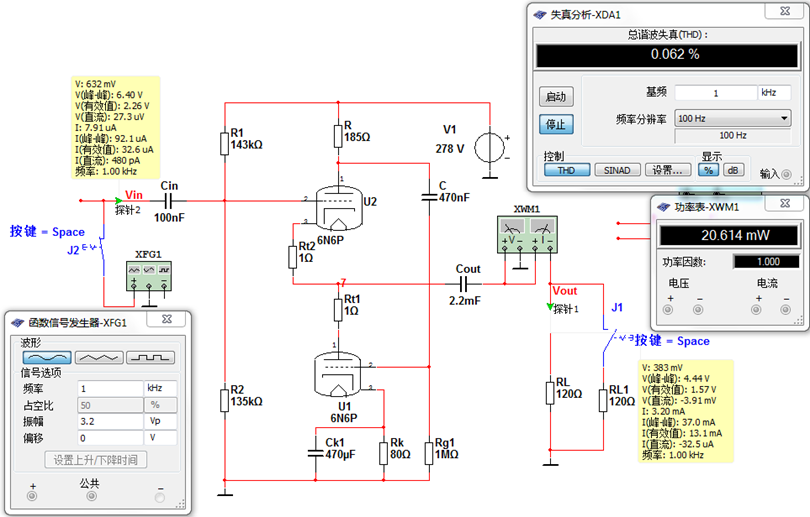
图11 输出20mw的测试结果

还可以进一步计算放大倍数和输出阻抗。

放大倍数\(A=\frac{Vout}{Vin}=\frac{2.7}{3.89}=0.69\)

输出阻抗的测量需要用到开关J1。

假设J1打开的情况下，测得的输出电压是U1；J1关闭的情况下，测得的输出电压为U2， 则输出阻抗\(Zo= RL*\frac{U1-U2}{2*U2-U1}\)，在本电路里可以测量并计算出Zo=50欧左右。

Cout的值和输出阻抗及负载有关。\(Cout = \frac{1}{2*π*f*(Zo + RL)}\)，假设下限频率取1HZ，则：

\(Cout =\frac{1}{ 2* 3.14 * 1*(50+120)}=937(uF)\)

考虑到它的耐压要高于电压电压，这一定是个巨无霸。但如果牺牲一点下限频率，那还是可以接受的。

下表是测量和计算的结果：

仿真测试结果

Vin(Vp)=

5.5

Vin(Vrms)=

3.89

Pout(mW）=

60.8

THD(%)=

0.19

Vout(Vrms)=

2.7

A=

0.69425

Vout@1/2RL(Vrms)=

2.07

Zout(KΩ)=

0.053

Vin(Vp)=

3.2

Vin(Vrms)=

2.26

Pout(mW）=

20.61

THD(%)=

0.062

Vout(Vrms)=

1.57

A=

0.693849

Vout@1/2RL(Vrms)=

1.25

Zout(KΩ)=

0.041

整体测试结果还比较理想：

60mw输出时的失真度<0.2%，已经达到<0.5%的要求。

20mw输出时的失真度0.062%，离设计目标<0.05%还有一些差距。需要通过引入环路负反馈来进一步降低失真。